 |
Главная |
Вывод уравнения Власова-Максвелла
|
из
5.00
|
Система уравнений Власова-Максвелла описывает движение частиц в собственном электромагнитном поле. Стартуем с обычного действия для электромагнитного поля[8], действия Власова-Максвелла или Лоренца (по повторяющимся верхним и нижним индексам идет суммирование):

 (4.1)
(4.1)

где Sр означает действие частиц (particles), Sf — действие полей (fields), Sp-f — действие частиц-полей (particles-fields).
Здесь а означает сорт частиц, отличаемый по массе mа и заряду еa, q нумерует частицы внутри сорта,  (q.t) (
(q.t) ( 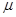 = 0,1.2,3; q =1,...,Na; a=1..... r) — 4 координаты q-й частицы copтa a, Au(x) — потенциал,
= 0,1.2,3; q =1,...,Na; a=1..... r) — 4 координаты q-й частицы copтa a, Au(x) — потенциал,  — электромагнитные поля,
— электромагнитные поля,  - метрика Минковского:
- метрика Минковского:  , т.е. диагональная матрица с 1 на первом месте и (-1) на остальных. Варьирование проводим специальным способом: сначала получаем движение частицы в поле, потом поля с заданными движениями частиц. Однако для частиц мы перейдем к функциям распределения, что и даст искомую систему уравнений.
, т.е. диагональная матрица с 1 на первом месте и (-1) на остальных. Варьирование проводим специальным способом: сначала получаем движение частицы в поле, потом поля с заданными движениями частиц. Однако для частиц мы перейдем к функциям распределения, что и даст искомую систему уравнений.
1. Варьирование Sp + Sp+f по координатам  (q.t)) даст уравнение движения зарядов в поле. Перепишем
(q.t)) даст уравнение движения зарядов в поле. Перепишем  для метрики Минковского (в дальнейшем греческие индексы
для метрики Минковского (в дальнейшем греческие индексы 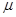 ,
,  пробегают четыре значения:
пробегают четыре значения: 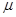 = 0,1,2,3; латинские i,j —три: i = 1,2,3):
= 0,1,2,3; латинские i,j —три: i = 1,2,3):

где Lp, — лагранжиан частиц.
Здесь  (i = 1,2,3) — трехмерный квадрат скорости, и мы учли, что х° = ct и вынесли с2 из-под корня. Проварьируем это выражение (опуская а):
(i = 1,2,3) — трехмерный квадрат скорости, и мы учли, что х° = ct и вынесли с2 из-под корня. Проварьируем это выражение (опуская а):

Варьируем Sp-f (снова опускаем а):


Отсюда из условия  = 0 получаем уравнение движения заряженной частицы в поле:
= 0 получаем уравнение движения заряженной частицы в поле:
уравнение больцман власов динамический модельный

где 
2. Уравнение для функции распределения получается как уравнение сдвига вдоль траекторий полученной динамической системы движения зарядов в поле. Видно, что удобно взять функцию распределения oт импульсов, а не от скоростей. При этом надо выразить скорости через импульсы:

Обозначая  получаем
получаем  =
=  Отсюда находим уравнение для функции распределения fa(x,p,t) (аналог 1.4):
Отсюда находим уравнение для функции распределения fa(x,p,t) (аналог 1.4):
 (4.2)
(4.2)
Здесь  Использовано, что
Использовано, что 
В это уравнение записано для ионов и электронов в следующем виде:
 (4.3)
(4.3)
Здесь fi(t, р, х) — функция распределения ионов по пространству и импульсам в момент времени t (i в (4.3) — первая буква слова ion. а не индекс), fе(t, р, х) — функция распределения электронов, ze — заряд иона, (—е) — заряд электрона, [v, B] — векторное произведение. Не выписано выражение v через р, однако часто его берут классическим: vаj = pj/ma , и тогда удобно записать уравнения через функцию распределения f(t, v, х) по скоростям вместо импульса. В записи (4.3) v надо брать различными для электронов и ионов, т.е. (4.3) требует уточнения, где vi , а где vc вместо v, и каковы эти функции, как функции импульса vi(p) и vc(p).
3. Уравнение для полей. Используем функцию распределения вместо плотности. Сначала надо переписать Sp-f через функцию распределения, совершив переход

после чего Sp-f запишется в виде

Теперь варьируем по потенциалам Аu(х):
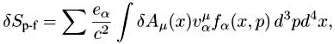

Полагаем  и получаем
и получаем
 (4.4)
(4.4)
Система (4.2), (4.4) и есть система уравнений Власова-Максвелла.
Замечание 1. Уравнения (4.4) являются второй парой уравнений Максвелла, а первая следует из равенств  что записывается в эквивалентном виде на языке дифференцирования кососимметрических тензоров
что записывается в эквивалентном виде на языке дифференцирования кососимметрических тензоров  Первая пара уравнений Максвелла записывается в виде
Первая пара уравнений Максвелла записывается в виде 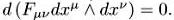
Замечание 2. При выводе уравнений Власова-Максвелла по схеме Боголюбова мы должны были бы стартовать с гамильтоновых систем с потенциалами Лиенарта-Вихерта (запаздывающие потенциалы). Для слабого релятивизма соответствующий лагранжиан называется лагранжианом Дарвина.
Замечание 3. Можно таким же способом получить уравнения Вла-сова-Янга-Миллса, заменив в четырех потенциалах Au числа на матрицы.
Вывод, Система уравнений Власова-Максвелла получается при варьировании действия электромагнетизма (действия Лоренца) с переходом к функции распределения. Уравнение для функции распределения получается как уравнение сдвига вдоль траекторий движения частиц.
|
из
5.00
|
Обсуждение в статье: Вывод уравнения Власова-Максвелла |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

