 |
Главная |
Математическая формализация задачи
|
из
5.00
|
В дальнейшем все функции времени предполагаются, если не оговорено противное, продолженными нулем на интервал (t < 0), а функции от r – на интервал (z < 0). Аргументы функции (или часть их) опускаются при записи, если это не приводит к недоразумению. Запись производной просто штрихом (или точкой) означает, что она взята по всему аргументу функции, а не по какой-либо его составляющей.
Задача, поставленная в предыдущем пункте, требует предварительного анализа, например, на предмет сокращения числа входящих в основные уравнения параметров – то есть, как минимум, приведения их к безразмерному виду. Проводя эту стандартную ( t= tτ, r= rρ, p= pπ, f = f ̃φ(τ, ρ, π), F = F̃Φ(τ, ρ, π), E(t, r) = EΕ(τ, ρ), J = JJ(τ, ρ), Sext = Qext/Q) операцию, видим, что между масштабными – взволнованными – коэффициентами должны иметь место стандартные же соотношения, дабы безразмерные уравнения не отличались по своей структуре от своих стартовых размерных аналогов. Таковыми являются: связь скорости и импульса (классическая или релятивистская); r = vt, причем, естественнее всегда брать c – за масштаб скоростей, а из t̃ и r̃ выбирать только одну.
В результате приходим к следующей системе соотношений, приводящих исходную систему к полностью безразмерному виду: один из параметров L = r̃, или T = t̃ является свободным, L = cT, P = p̃ = m0v0. Функции, входящие в систему, имеют своими масштабными коэффициентами следующие величины: Q̃ = 2N/(LTP), f ̃ = 2N/(LP), J̃= – |e|N/T, Ẽ = 4π|e|N, а единственный параметр, остающейся сомножителем перед Ε, – ε можно выразить как через начальные данные: ε = 4πreLN, так и через широко используемые (ωплаз)2 = 4πrec2n – плазменную частоту и νист = 1/T – частоту источника: ε = υ0(ωплаз/νист)2.
Приведенная таким образом к безразмерному виду исходная система приобретает вид:
 (1)
(1)
 (2)
(2)
Первой задачей анализа системы (1-2) будет получение явных формул для  путём разложения его в ряд по степеням ε, что сведёт дальнейшее решение уравнения (1) к решению классического уравнения первого порядка.
путём разложения его в ряд по степеням ε, что сведёт дальнейшее решение уравнения (1) к решению классического уравнения первого порядка.
3.4 Алгоритм разложения решения системы по параметру ε
Далее, на первом этапе исследования, при получении формул для E(t, z), нам потребуются производные всех порядков от временной компоненты источника F(t). Считаем, что она является действительной аналитической функцией. Зависимость v = v(p) полагаем аналитической по тем же причинам: как классическая, так и квантовая её модели, разумеется, этим свойством обладают, а для построения решения удобнее рассматривать сразу общий случай υ = υ(π) произвольного диффеоморфизма луча π > 0 на луч υ > 0 либо на интервал 0 < υ < υ0.
Поиск начального приближения  уравнения (1) приводит к формулам:
уравнения (1) приводит к формулам:

Далее, не обговаривая специально, удобно придерживаться следующих обозначений: χ = τ – ζ/υ, χ0 = τ – ζ/υ0, τ – (ζ – υ(τ – τ̃))/υ0 = χ̃0, χ̃ = χ.
Пусть  . Разложив по степеням ε произведение εE φ’ и приравнивая, друг другу коэффициенты при всех последовательных степенях, получаем, как обычно, бесконечную серию уравнений, зацепленных каждое только заодно другое своими правыми частями – последовательными источниками частиц, испытавших данное число взаимодействий (соударений). Начальное уравнение цепочки (с S0 = Sext для φ0) уже выписано. Основным для дальнейшего будет то, что левая часть у всех последующих уравнений одинакова. Правые части их имеют следующий вид:
. Разложив по степеням ε произведение εE φ’ и приравнивая, друг другу коэффициенты при всех последовательных степенях, получаем, как обычно, бесконечную серию уравнений, зацепленных каждое только заодно другое своими правыми частями – последовательными источниками частиц, испытавших данное число взаимодействий (соударений). Начальное уравнение цепочки (с S0 = Sext для φ0) уже выписано. Основным для дальнейшего будет то, что левая часть у всех последующих уравнений одинакова. Правые части их имеют следующий вид:  . Тождественность операторов
. Тождественность операторов  , порождающих все уравнения, позволяет следующим образом записать их решения φn, в операторной форме:
, порождающих все уравнения, позволяет следующим образом записать их решения φn, в операторной форме:  , где
, где  , а
, а  – это оператор сдвига по характеристике (невозмущённого) уравнения переноса: ζ → ζ – υ(τ – τn+1). Далее Εm – это оператор умножения на соответствующую функцию, а
– это оператор сдвига по характеристике (невозмущённого) уравнения переноса: ζ → ζ – υ(τ – τn+1). Далее Εm – это оператор умножения на соответствующую функцию, а  ; таким образом в развёрнутой записи имеем соотношение
; таким образом в развёрнутой записи имеем соотношение  . В последней формуле дифференцирования по dπ отмеченного υ = υ(π) НЕ производится.
. В последней формуле дифференцирования по dπ отмеченного υ = υ(π) НЕ производится.
На этом пути получаются весьма громоздкие явные выражения для поправок φn при малых n .
 Из них для J1(τ, χ0) и Ε1(τ, χ0) получаются весьма простые выражения: Подчеркнем, что простота полученных формул есть следствие того, что для данной задачи оператор обращения уравнений Максвелла
Из них для J1(τ, χ0) и Ε1(τ, χ0) получаются весьма простые выражения: Подчеркнем, что простота полученных формул есть следствие того, что для данной задачи оператор обращения уравнений Максвелла  – это просто интегрирование по dτ от 0 до τ. В результате и все поправки высших порядков выразятся как полиномы от τ с коэффициентами, зависящими только от Ε0(χ0) и её производных. Формула для Ε1(τ,χ0) уже выписана,
– это просто интегрирование по dτ от 0 до τ. В результате и все поправки высших порядков выразятся как полиномы от τ с коэффициентами, зависящими только от Ε0(χ0) и её производных. Формула для Ε1(τ,χ0) уже выписана,
Ε2(χ0)=  , а Ε3(χ0)=
, а Ε3(χ0)=
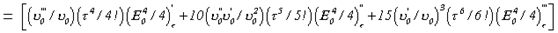
Далее естественно было предположить, что и общая формула для поправки к Ε(τ,χ0) порядка n будет иметь аналогичный вид:
Εn(τ,χ0) =  ,
,
где  – полином степени k от
– полином степени k от  , на что указывает показатель степени υ0 в знаменателях его коэффициентов. То, что получатся именно полиномы, а не мономы, как при малых n, угадывается при анализе характера упрощений в полученных формулах при переходе от функции распределения к току электронов; уже при n = 4 в коэффициент при
, на что указывает показатель степени υ0 в знаменателях его коэффициентов. То, что получатся именно полиномы, а не мономы, как при малых n, угадывается при анализе характера упрощений в полученных формулах при переходе от функции распределения к току электронов; уже при n = 4 в коэффициент при  , войдёт сумма A
, войдёт сумма A  + B
+ B  с наперед неизвестными значениями A и B.
с наперед неизвестными значениями A и B.
|
из
5.00
|
Обсуждение в статье: Математическая формализация задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

