 |
Главная |
Задания на прикидку и оценку в учебниках для 5–6 класса
|
из
5.00
|
Важным элементом вычислительной культуры является умение выполнять прикидку и оценку результата.
В настоящее время рекомендованы министерством образования и науки РФ следующие учебники по математике для 6 класса:
1. Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд Математика – М.: Мнемозина, 2003. – 304 с.
2. И.И. Зубарева, А.Г. Мордкович Математика 6 – М.:Мнемозина, 2006. – 264 с.
3. Г.В. Дорофеев, И.Ф. Шарыгин Математика 5–6
В основе умения выполнять прикидку лежит умение округлять числа. Потому-то этому вопросу в курсе математики 5–6 класса в учебнике под редакцией Г.В. Дорофеева уделяется достаточное внимание. С помощью упражнений закрепляется в сознании учащихся суть употребления основных терминов: «примерно», «приближенное равенство», «округление» и т.п.
Примеры (5 кл., №139,151,153):
1. В городе во время переписи населения было зарегистрировано 13882 жителя. Сообщая результаты переписи, одна газета указала, что в городе примерно 13 тысяч жителей, а другая – 14 тысяч. Какое сообщение точнее?
2. Миша задумал число и, округлив его до десятков, записал: 280. Какое число мог задумать Миша?
3. В школе 20 классов, в каждом из которых от 30 до 40 учеников. Оцените число учащихся школы. Какое из двух полученных чисел точнее указывает примерное число учащихся в школе, если в школе 758 учеников? 626 учеников?
При изучении темы «Округление десятичных дробей» также вначале округление осуществляется по смыслу, а затем по правилу округления. Учащимся предлагаются соответствующие группы упражнений. Среди них – задания на прикидку результата. Например, такие (6 кл., №459,469):
1. Выразите 1 тыс. секунд приближенно в часах. Какой из следующих ответов является лучшим приближением?
А. 2 ч. Б. 3 ч. В. 0,2 ч. Г. 0,3 ч.
2. Печенье, цена которого 26 руб. за 1 кг, расфасовано в пакеты. На упаковках указана их масса: 724 г., 615 г., 830 г. Какую стоимость для каждой упаковки, скорей всего, назовет продавец?
Важный класс задач, способствующих развитию вычислительных умений учащихся, базируется на использовании идеи сравнения. Например, в ряде случаев используется оценка суммы с опорой на умение сравнивать компоненты действия с некоторыми «рубежными» числами. Такие задачи и представлены в большинстве своем в учебнике Н.Я. Виленкина, но также присутствуют и в учебнике Г.В. Дорофеева.
Выделим приемы прикидки и оценки результата вычислений и соответствующие им задания в указанных выше учебниках.
В ряде случаев используется оценка суммы с опорой на умение сравнивать компоненты действия с некоторыми «рубежными» числами. В качестве таких чисел обычно выступают «круглые числа»: 10,100,1000 и т.п. Преимущественно в таких заданиях сравнивают сумму или произведение чисел с «рубежным» числом. Основная идея: сами числа, входящие в сумму или произведение заменить ближайшими к ним (например, округлить до целых десятичные дроби) «удобными» числами, которые легко можно сложить или умножить, а может быть и сразу заметить, что сумма или произведение заведомо меньше или больше «рубежного» числа. Подобные задания встречаются в учебниках Г.В. Дорофеева.
Примеры:
1. Пользуясь оценкой, сравните значение суммы 289+655 с 1000
Решение:
Необходимо прикинуть, что 1000 получается в результате сложения 300 и 700 (выбираем числа, которые ближе к слагаемым предложенной суммы). Заметим, что и 289<300, и 655<700, поэтому и вся сумма 289+655 меньше 1000.
2. Сравните с числом 10 сумму 2,901+2,809+2,999
Решение:
Замечаем, что каждое из слагаемых меньше трех, а значит их сумма заведомо меньше девяти, ну и, соответственно, меньше 10.
10>2,901+2,809+2,999
Кроме применения соответствующих правил, учащихся желательно учить сравнению чисел путем рассуждений. Это более завуалированный вариант сравнения с «рубежными» числами. Основная идея состоит в том, что это число не дано в задании, а дети его должны выявить сами. Этот прием можно использовать при сравнении обыкновенных дробей с разными знаменателями, т. к. такое сравнение можно осуществить проще и быстрее, нежели искать общий знаменатель, а потом сравнивать. Дроби удобно будет сравнивать с  и с 1. Не всегда можно использовать подобный прием, но во многих заданиях, он помогает экономить и время, и силы.
и с 1. Не всегда можно использовать подобный прием, но во многих заданиях, он помогает экономить и время, и силы.
При сравнении дробей с разными знаменателями на основе рассуждений и догадок можно разобрать сравнении таких пар чисел, как  и
и  ,
,  и
и  ,
, 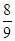 и
и  ,
,  и
и  :
:
1. Для дробей вида  и
и  в учебниках приводится даже вполне конкретное правило: «Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше». Поэтому, нетрудно установить, что
в учебниках приводится даже вполне конкретное правило: «Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше». Поэтому, нетрудно установить, что  >
> 
2. Сравнить дроби  и
и  немного сложней, но тем не менее, так же возможно, для этого нужно сравнить каждую из дробей с единицей. Замечаем, что дроби
немного сложней, но тем не менее, так же возможно, для этого нужно сравнить каждую из дробей с единицей. Замечаем, что дроби  не достает до единицы
не достает до единицы  , а дроби
, а дроби  не достает
не достает  . А
. А  и
и  сравнить проще.
сравнить проще.  >
>  , поэтому
, поэтому  расположено от единицы дальше, чем
расположено от единицы дальше, чем  .Значит,
.Значит,  <
<  .
.
3.  и
и  так же необходимо сравнивать с единицей, сразу заметив. Что
так же необходимо сравнивать с единицей, сразу заметив. Что  - неправильная дробь, которая всегда больше или равна единице, а
- неправильная дробь, которая всегда больше или равна единице, а  - дробь правильная, меньше единицы. Поэтому
- дробь правильная, меньше единицы. Поэтому  <
<  .
.
4. Прием сравнения таких дробей, как  и
и  , основан на сравнении каждой из дробей с половиной.
, основан на сравнении каждой из дробей с половиной.
 <
<  <
<  , т. к.
, т. к.  =
= 
Для отработки подобного приема можно использовать следующие задания:
1) Запишите дробь, равную  ; меньшую
; меньшую  и большую
и большую  , со знаменателем 10,12,50.
, со знаменателем 10,12,50.
2) Начертите координатную прямую (возьмите единичный отрезок равный 14 клеткам). Отметьте на координатной прямой все правильные дроби со знаменателем 7 и дробь  . Какие из отмеченных чисел меньше
. Какие из отмеченных чисел меньше  ? Какие из отмеченных чисел больше
? Какие из отмеченных чисел больше  ?
?
3) Выпишите дроби, которые больше  :
:
 ,
,  ,
,  ,
, 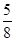 ,
,  ,
, 
4) Расположите дроби в порядке возрастания:
Прием второй «Сравнение путем рассуждений» (положительные и отрицательные числа)
При использовании такого приема сравнивают произведения чисел с нулем, с отрицательным числом, с положительным числом. Казалось бы, выполнение подобных упражнений полностью опирается на правило, ни о какой прикидке и речи не идет. Но, опять же находятся такие упражнения, которые отталкиваясь от правил, путем некоторых рассуждений, приводят нас фактически к необходимости выполнить их не вычисляя, а прикинув. Подобное задание встречается в учебнике Виленкина Н.Я и др. Этот пример будет подробнее разобран во второй главе моего диплома в одном из фрагментов урока.
Перед тем как сравнивать, нужно разобрать сравнение произведений с нулем в следующем виде:
· а – положительное число, b – отрицательное, сравните с нулем произведение аb.
Опираясь на правило умножения чисел с разными знаками, замечаем, что произведение положительного числа на отрицательное дает нам отрицательное число, а отрицательное число всегда меньше нуля. Следовательно, ab<0.
· а – отрицательное, b – отрицательное, сравните с нулем произведение ab.
Опираясь на правило умножение отрицательных чисел, замечаем, что произведение отрицательного числа на отрицательное дает нам положительное число, а положительное число всегда больше нуля. Следовательно, ab>0.
После выполнения такого задания рассматриваем сравнение в нулем конкретных произведений, уже не в общем виде:
· Поставьте вместо * знак < или > так, чтобы получилось верное равенство:
а)  ; в)
; в)  ; д)
; д)  ;
;
б) 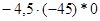 ; г)
; г)  ; е)
; е) 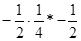 ;
;
Учитель предлагает выполнить это упражнение, не вычисляя. При выполнении пунктов а), б), д) полностью полагаемся на только что разобранные в общем виде случаи сравнения с нулем:
а) произведение отрицательного и положительного чисел дает нам отрицательное число, которое всегда меньше нуля;
б) произведение двух отрицательных чисел дает нам положительное число, которое всегда больше нуля;
д) аналогично, как и в пункте а), не смотря на то, что умножаем на дробь;
В пунктах в), г) и е) уже сравниваем с числом, но если в пункте в) такое сравнение осуществить совсем просто, не выполняя вычислений, то в пунктах г) и е) рассуждения будут немного сложней:
в) произведение положительного и отрицательного чисел дает нам отрицательное число, которое всегда меньше любого положительного;
г) Заметив, что в правой части произведение дает нам отрицательное число, знак все равно еще не можем поставить, т. к. в правой части тоже отрицательное число. Но есть одна особенность – сравним правую и левую часть, что общего можно отметить? «-8» есть и в правой, и в левой частях. Но, если в левой части оно взято всего один раз, то в правой целых 7,3 раза. Значит, на координатной прямой это число лежит левее числа -8. Поэтому  .
.
е) Случай, казалось бы, аналогичен пункту г) (проводятся аналогичные рассуждения), но особенность заключается в умножении дробей. Необходимо вспомнить, что при умножении двух обыкновенных дробей мы получаем дробь, меньшую каждого из множителей (можно включить умножение дробей в устный счет в начале урока, чтобы затем освежить в памяти эти сведения). Поэтому, дробь, полученная при умножении 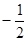 на
на  будет меньше, чем
будет меньше, чем  или
или  . Получаем
. Получаем  .
.
Этот прием больше используется в младшей школе при умножении многозначных чисел на однозначное или двузначное, но задания легко изменить таким образом, чтобы появилась возможность продолжить работать с таким приемом и в 5–6 классах. Достаточно натуральные числа заменить десятичными дробями, отчего суть приема не изменится.
В основе этого приема лежит знание таблицы умножения и навыки устного счета, а также используется округление чисел.
Главное, догадаться, что произведение чисел, не вычисляя можно определить по последней цифре числа, либо оценив произведение, округлив каждое из чисел до целых.
Примеры:
1) Догадайся! Как, не вычисляя значений произведений, выбрать из чисел, записанных справа, правильные ответы:
20,78 · 7 648,4
19,76 · 4 79,04
81,05 · 8 273,49
39,07 · 7 145,46
Школьники сначала умножают числа, стоящие в разряде сотых
(20,78 Ч 7 =?, 8 Ч7 = 56, результат 145,46), что дает основание предположить, какое из чисел второго столбика является значением данного произведения. Для последних двух выражений, значение произведения которых оканчивается цифрой 9 (7 Ч 7 = 49 и 1Ч9=9), во втором столбике есть два числа, имеющие в разряде сотых 9, в этом случае в качестве «прикидки» можно использовать прием округления (до целых).
2) Найди ошибки, не производя вычислений, способом «прикидки»:
80,04 Ч 9 = 72,36
99,8 Ч 8 = 7988,4
45,67 Ч 8 = 365,42
8,352 Ч 7 = 58,464
234,5 Ч 3 = 703,4
|
из
5.00
|
Обсуждение в статье: Задания на прикидку и оценку в учебниках для 5–6 класса |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

