Формула полной вероятности

Определение. Пусть задано некоторое вероятностное пространство (Ω, F, P). Тогда совокупность событий А₁, А₂, …, А_n называется полной группой событий, если выполняются следующие условия:

а) А₁ 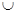 А₂ 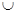 …, 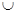А _n =Ω;

б) А _i 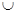A_j =Ø, ;

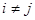г) Р(А_к)>0.

Пусть дано событие А, оно может наступить при появлении одного из несовместных Событий В₁, В₂,…, В _n, которые образуют полную группу. Нам также известны вероятности , , …, . Как можно найти вероятность события А? Ответ на этот вопрос дает теорема:

Теорема. Вероятность события А, которое может наступить лишь при условии появлении одного из несовместных событий В₁, В₂,…, В _n , образующих полную группу, равна сумме произведений вероятности каждого из этих событий на собственную условную вероятность:

P( А ) = .

Эту формулу также называют формулой полной вероятности.

Формула Бейеса

Составим задачу: Пусть дано событие А, оно может наступить при появлении одного из несовместных Событий В₁, В₂,…, В _n, которые образуют полную группу. Так как нам заранее не известно, какое событие наступит, их называют гипотезами. Допустим, что произведено испытание в результате, которого появилось событие А. Поставим своей задачей определить как изменились вероятности гипотез, в связи с тем что событие А уже наступило. Другими словами определим следующие условные вероятности:

, , …, .

Определить данные вероятности можно при помощи формулы Бейеса:

,

Заменив P( А ) = 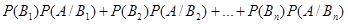 получим:

.

Решение задач.

Задача 1. Бросается игральный кубик. Какова вероятность того, что выпало число очков, больше трех (событие А), если известно, что выпала четная грань (событие В)?

Решение. Событию В соответствует выпадение чисел 2,4,6. Событию А выпадение чисел 4, 5, 6. Событию А В – 4, 6. Поэтому используя формулу условной вероятности получи:

.

Задача 2. Для контроля продукции лыжной фабрики из трех партий лыж взята на проверку одна деталь. Какова вероятность выявления бракованной продукции, если в одной партии 2/3 лыж бракованные, а в двух других все доброкачественные?

Решение. Пусть событие В= «Взятая деталь бракованная», А_к= «деталь берется из к-ой партии», тогда вероятность Р(А_к)=1/3, где к=1; 2; 3.

Пусть в первой партии находятся бракованные лыжи, значит 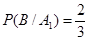, тогда в двух других парий нет бракованных лыж, то есть: . Применяя формулу полной вероятности получим:

P ( B )= .

Задача 3. Прибор состоит из двух узлов; работа каждого узла необходима для работы прибора в целом. Надежность (вероятность безотказной работы) в течении времени t первого узла равна p₁, второго р₂. Прибор испытывался в течении времени t, в результате чего обнаружено, что он отказал. Найдите вероятность того, что отказал первый узел, а второй исправен.

Решение. Пусть событие В= «прибор отказал», событие А₁= «Оба узла исправны», А₂= «первый узел отказал, а второй испарвен», А₃= «первый узел исправен, а второй узел отказал», А₄= «Оба узла отказали». Эти события образуют полную группу событий. Найдем их вероятности:

Р(А₁)=р₁р₂

Р(А₂)=(1-р₁)р₂

Р(А₃)=р₁(1-р₂)

Р(А₄)=(1-р₁)(1-р₂).

Так как наблюдалось событие В, то:

Р(В/А₁)=0,

Р(В/А₂)= Р(В/А₃)= 1.

Применяя формулу Бейеса получим:

.