Равномерное и равноускоренное движения

Равноускоренным движением тела называется движение, при котором его скорость за любые равные промежутки времени изменяется одинаково.

Если направление векторов 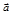 и 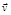 совпадают, движение называется равноускоренным, если противоположны – равнозамедленным.

При прямолинейном движении координатная ось обычно совмещается с направлением движения. Тогда при движении с постоянным ускорением координата и скорость материальной точки, при этом изменяются по кинематическим формулам:

,                                            (1.3.1)

.                                                     (1.3.2)

Путь, пройденный телом при равноускоренном движении:

,                                                     (1.3.3)

при равнозамедленном движении:

                  (1.3.4)

где ,  – модуль начальной скорости и модуль ускорения соответственно;  – путь пройденный телом до остановки; 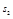 – путь, пройденный телом после остановки, при его движении в другую сторону.

Графическая иллюстрация соотношений (1.3.3) и (1.3.4) представлена на рисунках 5 и 6.

Движение тела с постоянным ускорением включает в себя равномерное и равноускоренное движение. При равномерном прямолинейном движении скорость тела не изменяется и в уравнениях (1.3.1), (1.3.2) и (1.3.3) нужно положить .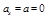

При плоском криволинейном движении мгновенная скорость тела в любой точке направлена по касательной к траектории, при этом ее проекции на оси координат и координаты материальной точки меняются со временем:

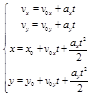                                           (3.1.5)

Простейшими случаями криволинейного движения являются движение тела, брошенного под углом к горизонту, и движение тела с постоянной по величине скоростью по окружности (см. §1.4.)

Если тело начинает движение в поле силы тяжести Земли со скоростью , составляющей угол  с горизонтом, то его траектория будет криволинейной, лежащей в плоскости перпендикулярной к поверхности земли. Удобно выбрать прямоугольную систему координат
с осью 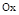, направленной горизонтально и осью , направленной вертикально (рис. 7). Движение представляет собой комбинацию равномерного движения в горизонтальном направлении и равнозамедленного и равноускоренного в вертикальном направлении с ускорением свободного падения .

Система начальных условий имеет вид:

. (1.3.6)

Проекции скорости на координатные оси c учетом (1.3.6) в любой момент времени 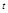 равны:

,                                             (1.3.7)

.                                              (1.3.8)

Из (1.3.7) и (1.3.8) получаем для модуля скорости

.                               (1.3.9)

Направление вектора скорости можно определить из соотношения

.                               (1.3.10)

Координаты тела в момент времени 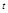 равны:

,                                                 (1.3.11)

.                                         (1.3.12)

Время полета до момента падения определяется из (1.3.12) при :

.                                                 (1.3.13)

Время подъема до максимальной высоты определяется из (1.3.8) при

.                                                          (1.3.14)

Максимальная высота подъема определяется из (1.3.12) при :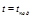

.                                               (1.3.15)

Дальность полета получаем из (1.3.11) при :

.                                                (1.3.16)

Исключая из (1.3.11) и (1.3.12) получаем уравнение траектории:

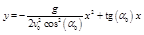.                                        (1.3.17)