 |
Главная |
Методический аспект решения задач по кинематике
|
из
5.00
|
При решении задач по кинематике необходимо выработать общие подходы к решению задач этого класса обобщенные в алгоритм решения задачи.
1. Внимательно прочитать задачу, проанализировать условие, выяснить характер движения.
2. Сделать схематический чертеж, отображающий описанное в задаче движение. Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения.
3. Выбрать систему отсчета.
4. Сформировать краткие данные задачи (выписать числовые значения заданных величин, ввести необходимые обозначения)
5. Составить для данного движения уравнения, отражающие математическую связь между проекциями векторов на оси координат. (Число уравнений должно быть равно числу неизвестных величин).
6. Решить составленную систему относительно искомых величин (получить расчетные формулы).
7. Подставить в расчетные формулы числовые значения физических величин и произвести вычисления. Оценить реальность полученного результата.
1.6. Контрольные вопросы
1. Что называют системой отсчета?
2. При каких условиях тело можно рассматривать как материальную точку?
3. Как определить координаты точки на плоскости, в пространстве?
4. Как по координатам двух точек на плоскости определить расстояние между ними?
5. Сумма какого минимального числа векторов неодинаковой длины может равняться нулю?
6. Что такое механическое движение? Какое движение тела называют поступательным?
7. Что называют траекторией движения материальной точки?
8. Зависит ли траектория движения от выбора системы отсчета?
9. Что такое вектор перемещения, скорости, ускорения?
10. Что называют длиной пути?
11. Может ли модуль вектора перемещения материальной точки быть больше пути, пройденного ей за тот же промежуток времени?
12. Что показывает счетчик километров автомобиля (путь или перемещение)?
13. Что такое мгновенная и средняя скорость?
14. Какую скорость (мгновенную, среднюю) показывает спидометр автомобиля?
15. Какое движение называют равномерным?
16. Если известна траектория движения, можно ли указать направление мгновенной скорости и ускорения в произвольной точке этой траектории?
17. Может ли материальная точка в один и тот же момент времени иметь: скорость, направленную вправо, и ускорение направленное влево; равную нулю скорость и не равное нулю ускорение?
18. Как по графику зависимости скорости от времени для прямолинейного движения найти перемещение материальной точки и пройденный ей путь?
19. Какое движение называют равноускоренным?
20. Как выглядит график зависимости скорости от времени для равноускоренного прямолинейного движения материальной точки?
21. Какое движение называют свободным падением?
22. В какой точке траектории скорость снаряда составляет с его ускорением прямой угол? (Сопротивлением воздуха пренебречь).
23. В какой точке траектории снаряд имеет наименьшую скорость, наименьшее ускорение?
24. Какой может быть траектория материальной точки, если она движется с постоянным по величине и направлению ускорением?
25. Что такое угловая скорость и как она связана с частотой и периодом обращения при движении по окружности?
26. Зависит ли угловая скорость и ускорение точек равномерно вращающегося диска от расстояния до оси вращения?
27. При каком движении мгновенная скорость материальной точки в любой момент времени перпендикулярна ускорению?
28. Могут ли совпадать направления мгновенной скорости и ускорения при движении по криволинейной траектории?
29. При движении по окружности модуль скорости движения материальной точки возрастает. Будет ли ускорение направлено к центру окружности?
30. Какие точки колеса телеги имеют наибольшее и наименьшее значение скорости относительно Земли и относительно телеги?
31. Поезд движется прямолинейно с ускорением 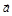 . Чему равно ускорение камня выброшенного из окна вагона относительно поезда и относительно Земли?
. Чему равно ускорение камня выброшенного из окна вагона относительно поезда и относительно Земли?
32. В чем состоит принцип независимого движения тел?
Примеры решения задач
Пример 1. По взаимно перпендикулярным дорогам движутся два автомобиля с постоянными скоростями  и
и  . В момент начала наблюдения первый автомобиль находился на перекрестке, а второй на расстоянии
. В момент начала наблюдения первый автомобиль находился на перекрестке, а второй на расстоянии  от него. Определить наименьшее расстояние между автомобилями.
от него. Определить наименьшее расстояние между автомобилями.
РЕШЕНИЕ:
Дано:

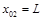



| Схема задачи:
Решение: Запишем законы движения для каждого из тел в координатной форме:
с учетом данных задачи получим
Расстояние между точками определим
с учетом (2), имеем
Найдем момент времени
Находя производную и приравнивая ее к нулю, получаем уравнение:
Из (6) находим
Подстановка (7) в (4) дает ответ задачи
Ответ: | |||
Найти:

|
Пример 2. Лифт поднимается с ускорением  , В тот момент, когда его скорость стала равна
, В тот момент, когда его скорость стала равна  , с потолка лифта начал падать болт. Высота лифта
, с потолка лифта начал падать болт. Высота лифта  . Вычислить время падения болта и расстояние, пройденное болтом относительно шахты.
. Вычислить время падения болта и расстояние, пройденное болтом относительно шахты.
РЕШЕНИЕ:
Дано:





|
Решение: Рассмотрим движение болта (точка Б – индексы «2») и точки пола лифта (точка Л – индексы «1») относительно шахты.
Запишем законы движения для каждой точки в координатной форме:
с учетом данных задачи получим
В момент падения болта на пол
с учетом (2) имеем
Найдем время
Расстояние, пройденное болтом относительно шахты:
Из (6) с учетом (2) и (5) находим
Подстановка числовых данных в (5) и (7) дает числовой ответ задачи.
Ответ: |
Найти:


|
Пример 3. Со скалы высоты  в горизонтальном направлении бросают тело с начальной скоростью
в горизонтальном направлении бросают тело с начальной скоростью  . Одновременно с поверхности земли под углом
. Одновременно с поверхности земли под углом  к горизонту навстречу бросают второе тело с такой же начальной скоростью. Определить на каком расстоянии от скалы бросали второе тело, если тела столкнулись в воздухе. Определить скорость второго тела относительно первого.
к горизонту навстречу бросают второе тело с такой же начальной скоростью. Определить на каком расстоянии от скалы бросали второе тело, если тела столкнулись в воздухе. Определить скорость второго тела относительно первого.
РЕШЕНИЕ:
Дано:



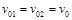

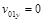




| Схема задачи:
Решение: С учетом начальных условий законы движения тел можно записать в виде:
В момент «встречи» тел
или с учетом (1)
Исключив из системы уравнений (3) время, найдем
Закон изменения скорости для каждого тела, с учетом начальных условий имеет вид
Относительная скорость движения
или в проекциях
Модуль относительной скорости определим как
Окончательно, при подстановке (7) в (8) получим
Ответ: | |||
Найти:


|
Пример 4. Шарик радиуса  катится со скоростью
катится со скоростью  по двум рельсам, расположенным на расстоянии
по двум рельсам, расположенным на расстоянии  . Определить скорости верхней (А) и нижней (B) точек шара относительно рельсов.
. Определить скорости верхней (А) и нижней (B) точек шара относительно рельсов.
РЕШЕНИЕ:
Дано:



|
Решение: Мгновенная ось вращения в данном случае определена на рисунке (
где
Скорости точек А и В определим как
С учетом (1) и (2) из (3), найдем
Подставляя в (4) числовые значения величин, получим
Ответ: | |||
Найти:
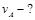

|
|
из
5.00
|
Обсуждение в статье: Методический аспект решения задач по кинематике |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


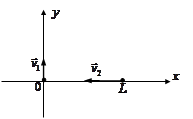
 ,
,  ; (1)
; (1) ,
,  . (2)
. (2) , (3)
, (3)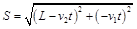 . (4)
. (4) соответствующий минимуму расстояния между телами. Условие минимума расстояния имеет вид
соответствующий минимуму расстояния между телами. Условие минимума расстояния имеет вид . (5)
. (5) . (6)
. (6) . (7)
. (7) . (8)
. (8)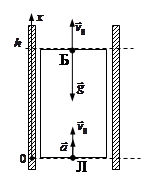 Схема задачи:
Схема задачи: ,
,  ; (1)
; (1) ,
,  . (2)
. (2) , (3)
, (3) . (4)
. (4)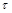
 . (5)
. (5) , (6)
, (6) . (7)
. (7) ,
,  .
.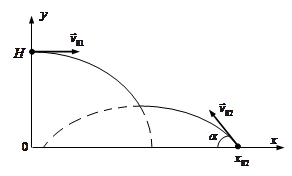
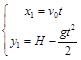 ,
,  . (1)
. (1) , (2)
, (2) . (3)
. (3) . (4)
. (4) ,
,  . (5)
. (5) равна:
равна: , (6)
, (6) . (7)
. (7) . (8)
. (8)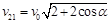 . (9)
. (9)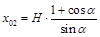 ,.
,.  .
. Схема задачи:
Схема задачи:
 ). Угловая скорость шара относительно мгновенной оси
). Угловая скорость шара относительно мгновенной оси , (1)
, (1) . (2)
. (2) (3)
(3) . (4)
. (4) . (5)
. (5)