Поступательное движение и его характеристики

Механическим движением тела называется изменение его положения в пространстве с течением времени относительно других тел или его отдельных частей.

Механическое движение относительно, т.е. если говорить, что тело совершает механическое движение, то необходимо указать тело отсчета, относительно которого происходит это движение.

В классической механике рассматриваются механические движения тел, происходящие со скоростями, значительно меньшими скорости света в вакууме ( ).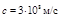

Для описания механического движения необходимо указать тело, относительно которого рассматривается движение. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчета. С телом отсчета связывается система координат. Чаще всего для определения положения тела используется правая декартова прямоугольная система координат.

Система отсчёта – совокупность тела отсчёта и связанная с этим телом система координат и прибор для измерения времени (часы).

Тело, размерами, формой и структурой которого можно пренебречь при изучении данного механического движения, называется материальной точкой.

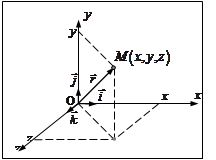Положение материальной точки М задаётся либо радиус-вектором 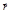, проведенным из начала системы координат:

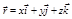,    (1.2.1)

либо координатами 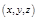 (рис. 1).

При движении точки радиус-вектор и координаты изменяются с течением времени. Говорят, что задан закон движения, если известна векторная функция времени

                   Рис. 1 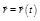                                                                 (1.2.2)

или три эквивалентные ей скалярные функции:

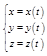                                      (1.2.3)

Линия, описываемая движущейся точкой в пространстве, называется траекторией. Движения разделяются на прямолинейные и криволинейные в зависимости от вида траектории.

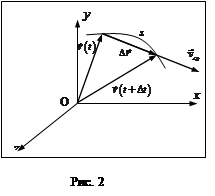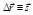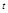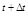Перемещение точки за промежуток времени  – вектор , соединяющий положения точки в моменты  и . Из
рис, 2 видно, что

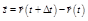(1.2.4)

Путь 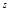, пройденный точкой за тот же промежуток времени , это длина соответствующего отрезка траектории. При прямолинейном движении в одном направлении 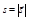, при криволинейном – .

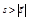Путь 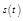, пройденный точкой к моменту времени 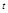, это длина траектории от некоторого начального положения до положения
в момент 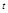. Если точка меняла направление движения по той же траектории, то её путь  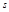– это полное расстояние, пройденное вдоль траектории.

Вектором средней скорости за время  называется отношение вектора перемещения материальной точки ко времени, за которое оно совершено:

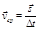                                                   (1.2.5)

Направление вектора 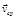 совпадает с  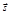(рис. 2).

Средней путевой скоростью за время называется скалярная величина равная отношению отрезка пути 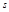 к

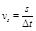                                                    (1.2.6)

При прямолинейном движении в одном направлении 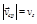, при криволинейном – .

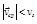Мгновенная скорость в данной точке траектории равна пределу отношения перемещения на участке траектории, включающем эту точку, к промежутку времени, в течение которого это перемещение совершается:

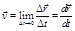.                                               (1.2.7)

Скорость в каждой точке направлена по касательной к траектории. Проекции скорости на оси координат:

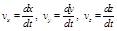,                                 (1.2.8)

модуль скорости

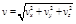,                                               (1.2.9)

причем

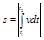,                                          (1.2.10)

где 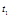 и 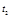 – фиксированные моменты времени при движении тела по заданной траектории.

В случае произвольного криволинейного движения вектор скорости 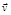 может изменяться с течением времени как по модулю, так и по направлению (рис. 3).

Вектором среднего ускорения за время  называется отношение приращения вектора скорости 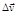 ко времени, за которое оно совершено:

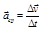,                                          (1.2.11)

Направление вектора 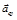 совпадает с направлением  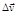(рис. 3).

Предельный переход в выражении (1.2.11) при 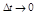, определяет вектор ускорения материальной точки в момент времени :

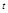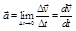. (1.2.12)

Проекции вектора ускорения на координатные оси равны:

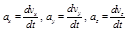, (1.2.13)

модуль ускорения

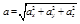.                                              (1.2.14)

Если движение материальной точки плоское (будем считать, что траектория материальной точки лежит в плоскости 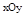), то вектор ускорения  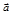всегда можно разложить на две взаимно перпендикулярные составляющие (рис. 4)

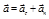,                                                        (1.2.15)

где 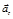 – тангенциальное (касательное) и  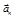– нормальное (центростремительное) ускорения материальной точки.

Вектор 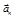 всегда направлен к центру кривизны траектории О', а вектор  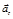лежит на касательной к траектории и может быть направлен как в сторону движения, так и в противоположную сторону.

Нормальное ускорение 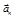 характеризует быстроту изменения направления вектора скорости материальной точки. Тангенциальное ускорение
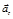 характеризует быстроту изменения величины скорости материальной точки.

Абсолютные значения нормального и тангенциального ускорений определяются соотношениями

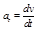,                                                            (1.2.16)

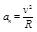,                                                            (1.2.17)

где 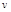 модуль скорости материальной точки;  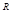— радиус кривизны траектории в данный момент времени.

Абсолютные значения величин ускорений связаны между собой соотношением

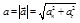.                                              (1.2.18)