 |
Главная |
Равномерное движение по окружности
|
из
5.00
|
Движение по окружности – простейший пример криволинейного движения. Скорость 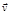 движения по окружности называется линейной скоростью. При равномерном движении по окружности модуль
движения по окружности называется линейной скоростью. При равномерном движении по окружности модуль 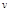 мгновенной скорости материальной точки с течением времени не изменяется (
мгновенной скорости материальной точки с течением времени не изменяется ( 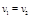 на рис. 8).
на рис. 8).
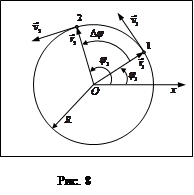 Изменение положения точки на окружности может быть охарактеризовано изменением угловой координаты точки:
Изменение положения точки на окружности может быть охарактеризовано изменением угловой координаты точки: 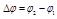 . Угол
. Угол 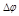 называется углом поворота радиус-вектора точки (рис. 8).
называется углом поворота радиус-вектора точки (рис. 8).
При равномерном движении точки по окружности за любые равные промежутки времени углы поворота её радиус-вектора одинаковы. Поэтому угловой скоростью 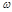 движения точки
движения точки
по окружности вокруг заданного
центра (или оси) называется отношение угла поворота 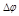 радиус-вектора точки за промежуток времени
радиус-вектора точки за промежуток времени 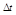 к длительности этого промежутка:
к длительности этого промежутка:
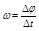 . (1.4.1)
. (1.4.1)
Угол поворота 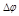 радиус-вектора точки, равномерно движущемся по окружности, равен:
радиус-вектора точки, равномерно движущемся по окружности, равен:
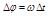 . (1.4.2)
. (1.4.2)
Промежуток времени 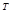 , в течение которого точка совершает один полный оборот по окружности, называется периодом обращения (периодом вращения), а величина обратная периоду
, в течение которого точка совершает один полный оборот по окружности, называется периодом обращения (периодом вращения), а величина обратная периоду
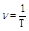 (1.4.3)
(1.4.3)
– частотой вращения.
За один период угол поворота радиус-вектора точки равен 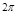 рад, поэтому
рад, поэтому
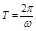 , (1.4.4)
, (1.4.4)
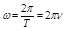 . (1.4.5)
. (1.4.5)
Путь 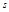 , пройденный точкой, равномерно движущейся по окружности, за промежуток времени
, пройденный точкой, равномерно движущейся по окружности, за промежуток времени 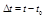 при
при 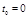 равен
равен 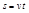 . Путь, пройденный точкой за один период по окружности радиуса
. Путь, пройденный точкой за один период по окружности радиуса 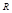 , равен
, равен 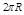 , а угол поворота радиус-вектора точки за тот же промежуток времени равен
, а угол поворота радиус-вектора точки за тот же промежуток времени равен 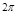 рад. Отсюда находим связь между линейной и угловой скоростью:
рад. Отсюда находим связь между линейной и угловой скоростью:
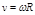 . (1.4.6)
. (1.4.6)
Всякое перемещение плоской фигуры, происходящее в плоскости расположения этой фигуры, можно рассматривать в любой момент времени как результат наложения поступательного движения тела вместе с некоторой произвольной точкой  тела (называемой полюсом) и вращательного движения тела относительно этой точки.
тела (называемой полюсом) и вращательного движения тела относительно этой точки.
Выбирая полюс в различных точках тела, можно по-разному осуществлять разложение плоского движения на поступательное и вращательное. В каждом из этих случаев перемещение и скорость в поступательном движении могут быть различными, а угловое перемещение и угловая скорость одинаковые.
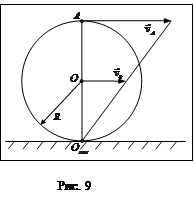 |
В случае плоско-параллельного движения твердого тела существует такая точка, скорость которой в данный момент времени равна нулю. Эту точку называют мгновенным центром скоростей. Мгновенный центр скоростей можно найти по следующим рекомендациям:
1. при качении без проскальзывания плоской фигуры по неподвижной поверхности мгновенный центр скоростей совпадает с точкой соприкосновения тела с поверхностью
(рис 9).
2. мгновенный центр скоростей находится на пересечении перпендикуляров, восставленных из двух данных точек тела к линиям векторов абсолютной скорости этих точек.
3. в том случае, когда перпендикуляры, проведенные из указанных точек сливаются, сливаются в один, мгновенный центр скоростей лежит в точке пересечения перпендикуляра с линией, проведенной через концы векторов скоростей этих
точек (рис. 9).
|
из
5.00
|
Обсуждение в статье: Равномерное движение по окружности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

