 |
Главная |
Понятие о решение задачи Дирихле для уравнения Лапласа методом Монте-Карло
|
из
5.00
|
Пусть на плоскости  дана область
дана область  с кусочно-гладкой границей
с кусочно-гладкой границей  . В области
. В области  построим квадратную сетку
построим квадратную сетку  с шагом
с шагом  :
:
 , (1)
, (1)
Мы предполагаем, что сетка  состоит из внутренних узлов и граничных узлов первого рода. Граничные узлы сетки
состоит из внутренних узлов и граничных узлов первого рода. Граничные узлы сетки  образуют ее границу
образуют ее границу  . Грубо говоря, граница
. Грубо говоря, граница 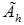 представляет собой линейный ряд точек
представляет собой линейный ряд точек  , аппроксимирующий криво-криволинейную границу
, аппроксимирующий криво-криволинейную границу  области
области  с точностью до
с точностью до  .
.
Представим себе частицу  , которая совершает равномерное случайное блуждание по узлам сетки (1). А именно, находясь во внутреннем узле
, которая совершает равномерное случайное блуждание по узлам сетки (1). А именно, находясь во внутреннем узле  сетки
сетки  , эта частица за один переход с одной и той же вероятностью, равной 1/4, может переместиться в один из четырех соседних узлов: или в
, эта частица за один переход с одной и той же вероятностью, равной 1/4, может переместиться в один из четырех соседних узлов: или в  (шаг влево), или в
(шаг влево), или в  (шаг вправо), или в
(шаг вправо), или в  (шаг вниз), или в
(шаг вниз), или в  (шаг вверх), причем каждый такой единичный переход совершенно случаен и не зависит от положения частицы и ее прошлой истории. Будем считать, что блуждание частицы
(шаг вверх), причем каждый такой единичный переход совершенно случаен и не зависит от положения частицы и ее прошлой истории. Будем считать, что блуждание частицы  заканчивается, как только эта частица попадет на границу
заканчивается, как только эта частица попадет на границу 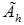 ; в этом смысле граница
; в этом смысле граница  представляет собой «поглощающий экран». Можно доказать, что с вероятностью, равной 1, блуждание точки
представляет собой «поглощающий экран». Можно доказать, что с вероятностью, равной 1, блуждание точки  через конечное число шагов заканчивается на границе.
через конечное число шагов заканчивается на границе.
Если частица  начала свое блуждание с фиксированной внутренней точки
начала свое блуждание с фиксированной внутренней точки  сетки
сетки  , то конечная совокупность последовательных положений этой частицы:
, то конечная совокупность последовательных положений этой частицы:  где
где  и
и  , называется траекторией частицы (с
, называется траекторией частицы (с  шагами) или историей блуждания.
шагами) или историей блуждания.
Равномерное случайное блуждание частицы на плоскости можно организовать с помощью равномерно распределенной последовательности одноразрядных случайных чисел, принимающих значения  . Для этого, например, достаточно производить розыгрыш, т. е. случайную выборку из чисел
. Для этого, например, достаточно производить розыгрыш, т. е. случайную выборку из чисел  , придерживаясь инструкции, указанной в таблице 1 (Приложение B); причем числа 8 и 9 переигрываются.
, придерживаясь инструкции, указанной в таблице 1 (Приложение B); причем числа 8 и 9 переигрываются.
Случайные числа берутся из готовых таблиц или вырабатываются электронной машиной. Последний способ при работе на счетной машине предпочтительнее, так как он позволяет не загружать сильно память машины.
Пусть в точках границы Г области G определена некоторая функция  . Перенесем эти значения на границу
. Перенесем эти значения на границу  сетки
сетки  . Например, для каждого граничного узла
. Например, для каждого граничного узла  определим ближайшую по горизонтали (или вертикали) точку
определим ближайшую по горизонтали (или вертикали) точку  и положим
и положим
 .
.
Для краткости введем обозначение
 .
.
Пусть 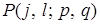 – вероятность того, что траектория частицы, вышедшей из узла
– вероятность того, что траектория частицы, вышедшей из узла  сетки
сетки  , закончится в граничном узле
, закончится в граничном узле  . Так как блуждание точки неизбежно заканчивается на границе
. Так как блуждание точки неизбежно заканчивается на границе  в первой же точке выхода ее на границу, то
в первой же точке выхода ее на границу, то
 , (2)
, (2)
где суммирование распространяется на все точки  границы
границы  , причем
, причем
 (3)
(3)
где  – граничный узел.
– граничный узел.
Составим сумму
 , (4)
, (4)
где точка  пробегает всю границу
пробегает всю границу  . Если функцию
. Если функцию  рассматривать как случайную величину, принимающую значения
рассматривать как случайную величину, принимающую значения 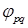 на границе
на границе  , то сумма (4) представляет собой математическое ожидание (среднее значение) функции
, то сумма (4) представляет собой математическое ожидание (среднее значение) функции 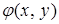 на границе
на границе 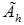 для траекторий, начинающихся в точке
для траекторий, начинающихся в точке  («премия за выход на границу» из начальной точки
(«премия за выход на границу» из начальной точки  ). Частица, начавшая свое случайное блуждание из внутреннего узла
). Частица, начавшая свое случайное блуждание из внутреннего узла  , после первого шага с вероятностью, равной 1/4, попадает в один из четырех соседних узлов. Поэтому случайные блуждания, начинающиеся в узле
, после первого шага с вероятностью, равной 1/4, попадает в один из четырех соседних узлов. Поэтому случайные блуждания, начинающиеся в узле  , в зависимости от вида траекторий распадаются на четыре категории новых случайных блужданий:
, в зависимости от вида траекторий распадаются на четыре категории новых случайных блужданий:

По формуле полной вероятности имеем
 (5)
(5)
Отсюда, умножая обе части равенства (5) на граничные значения  и суммируя по всем возможным значениям
и суммируя по всем возможным значениям  и
и  , на основании формулы (4) получим
, на основании формулы (4) получим
 . (6)
. (6)
Кроме того, в силу формулы (3) имеем
 , (7)
, (7)
если точка  .
.
Рассмотрим теперь задачу Дирихле об отыскании функции  , гармонической области
, гармонической области  и принимающей на ее границе
и принимающей на ее границе  заданные непрерывные значения
заданные непрерывные значения  . Согласно методу сеток эта задача сводится к нахождению значений
. Согласно методу сеток эта задача сводится к нахождению значений  искомой функции
искомой функции 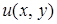 во внутренних узлах
во внутренних узлах  некоторой сетки
некоторой сетки  при условии, что значения в граничных узлах
при условии, что значения в граничных узлах  известны и равны
известны и равны 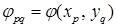 . Неизвестные
. Неизвестные  определяются из системы линейных уравнений
определяются из системы линейных уравнений
 (8)
(8)
Сравнивая формулы (8) с формулами (6), (7), мы усматриваем, что они совпадают с точностью до обозначений. Следовательно, искомые неизвестные  можно рассматривать как математические ожидания
можно рассматривать как математические ожидания  . Величины
. Величины  допускают экспериментальное определение. Рассмотрим достаточно большое число
допускают экспериментальное определение. Рассмотрим достаточно большое число 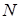 равномерных случайных блужданий частицы по узлам сетки
равномерных случайных блужданий частицы по узлам сетки  , исходящих из фиксированного узла
, исходящих из фиксированного узла  и заканчивающихся на границе
и заканчивающихся на границе  . Пусть
. Пусть  соответствующие точки выхода частицы на границу
соответствующие точки выхода частицы на границу  . Заменяя математическое ожидание
. Заменяя математическое ожидание  эмпирическим математическим ожиданием, будем иметь
эмпирическим математическим ожиданием, будем иметь
 . (9)
. (9)
Формула (9) дает статистическую оценку величины  и может быть применена для приближенного решения задачи Дирихле. Метод решения задач, основанный на использовании случайных величин, получил общее название метода Монте-Карло.
и может быть применена для приближенного решения задачи Дирихле. Метод решения задач, основанный на использовании случайных величин, получил общее название метода Монте-Карло.
Заметим, что с помощью формулы (9) можно непосредственно найти приближенное значение  решения задачи Дирихле в единственной фиксированной точке
решения задачи Дирихле в единственной фиксированной точке  сетки
сетки  , не зная решения задачи для остальных точек сетки. Этим обстоятельством метод Монте-Карло для задачи Дирихле резко отличается от обычных стандартных способов решения этой задачи.
, не зная решения задачи для остальных точек сетки. Этим обстоятельством метод Монте-Карло для задачи Дирихле резко отличается от обычных стандартных способов решения этой задачи.
Интересно отметить, что вероятность  , в силу формулы (4), представляет собой аналог функции Грина для задачи Дирихле в области
, в силу формулы (4), представляет собой аналог функции Грина для задачи Дирихле в области  . Эта величина может быть найдена экспериментально на основании формулы (9), если задать следующие граничные условия:
. Эта величина может быть найдена экспериментально на основании формулы (9), если задать следующие граничные условия:
 .
.
Построив такую функцию Грина, мы получаем возможность, применяя формулу (9), просто
находить приближенное решение задачи Дирихле для области  данной границей
данной границей  при любых граничных значениях
при любых граничных значениях  .
.
Недостатком рассмотренного варианта метода Монте-Карло для задачи Дирихле является слабая сходимость по вероятности при  эмпирического математического ожидания
эмпирического математического ожидания

к математическому ожиданию  . Чтобы устранить это неблагоприятное обстоятельство, используют различные модификации случайных блужданий. Кроме того, при решении задачи полезно учитывать также, что блуждание частицы
. Чтобы устранить это неблагоприятное обстоятельство, используют различные модификации случайных блужданий. Кроме того, при решении задачи полезно учитывать также, что блуждание частицы  , начинающееся в точке
, начинающееся в точке 
автоматически является случайным блужданием частицы, начинающимся в любой промежуточной точке траектории этой частицы.
|
из
5.00
|
Обсуждение в статье: Понятие о решение задачи Дирихле для уравнения Лапласа методом Монте-Карло |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

