 |
Главная |
Задача Дирихле для уравнения Пуассона и ее решение методом Монте-Карло с использованием метода сеток
|
из
5.00
|
В ограниченной связной области  плоскости
плоскости  с простой границей
с простой границей  рассмотрим дифференциальной уравнение с частными производными
рассмотрим дифференциальной уравнение с частными производными
 (1)
(1)
где  – искомая функция. Уравнение (1) при
– искомая функция. Уравнение (1) при  называется уравнением Лапласа, а при
называется уравнением Лапласа, а при  – уравнением Пуассона.
– уравнением Пуассона.
Применяя метод сеток для решения краевых задач, прежде всего появляется задача замены дифференциальных уравнений разностными уравнениями. Аппроксимации дифференциального уравнения разностным заключается в том, что производные, входящие в дифференциальное уравнение, заменяются линейными комбинациями значений функции  в узлах сетки по тем или иным формулам численного дифференцирования. В зависимости от того, какими формулами численного дифференцирования будем пользоваться, получим различную точность аппроксимации дифференциального уравнения разностным.
в узлах сетки по тем или иным формулам численного дифференцирования. В зависимости от того, какими формулами численного дифференцирования будем пользоваться, получим различную точность аппроксимации дифференциального уравнения разностным.
Предположим, что на границе  задана некоторая функция
задана некоторая функция 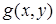 (часто пишут g( S), где
(часто пишут g( S), где  — длина дуги границы, отсчитываемая от какой-нибудь фиксированной точки). Требуется найти такое решение
— длина дуги границы, отсчитываемая от какой-нибудь фиксированной точки). Требуется найти такое решение  уравнения (1), которое на границе совпадает с
уравнения (1), которое на границе совпадает с  :
:
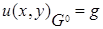 . (2)
. (2)
Задачу об отыскании решения уравнения
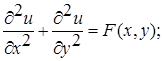 (3)
(3)
удовлетворяющего граничному условию, называют задачей Дирихле для уравнения Пуассона.
Для приближенного решения этой задачи выбирают на плоскости достаточно мелкую квадратную сетку 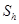 с шагом
с шагом 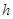 (рис.1, Приложение А). Координаты узлов этой сетки пусть будут
(рис.1, Приложение А). Координаты узлов этой сетки пусть будут  , а значения
, а значения  для краткости обозначим
для краткости обозначим  и
и 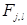 . Узел
. Узел  называют внутренним, если и он, и все четыре соседних с ним узла
называют внутренним, если и он, и все четыре соседних с ним узла  принадлежат
принадлежат  , в противном случае узел
, в противном случае узел 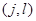 , принадлежащей
, принадлежащей  называют граничным.
называют граничным.
Во внутреннем узле 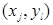 уравнение заменим разностным
уравнение заменим разностным
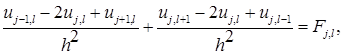 (4)
(4)
которое перепишем в виде
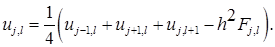 (5)
(5)
В граничных узлах
 . (6)
. (6)
Решение алгебраической системы при 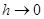 приближается к решению задачи Дирихле для уравнения (1).
приближается к решению задачи Дирихле для уравнения (1).
Перенумеруем все узлы, принадлежащие  (в произвольном порядке), и перепишем в том же порядке уравнения (3), (4). Тогда получим систему вида
(в произвольном порядке), и перепишем в том же порядке уравнения (3), (4). Тогда получим систему вида
 (7)
(7)
Матрица этой системы имеет следующую структуру: внутреннему узлу с номером  отвечает строка
отвечает строка  , в котором четыре элемента равны ¼, а остальные – нули; граничному узлу с номером
, в котором четыре элемента равны ¼, а остальные – нули; граничному узлу с номером 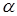 отвечает строка
отвечает строка  ; все диагональные элементы
; все диагональные элементы  =0. (Все собственные значения такой матрицы по абсолютной величине меньше единицы.) Свободные члены этой системы
=0. (Все собственные значения такой матрицы по абсолютной величине меньше единицы.) Свободные члены этой системы  , если узел
, если узел 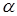 внутренний, и
внутренний, и  , если узел
, если узел  граничный.
граничный.
Один из методов решения системы (5) является метод Монте-Карло. Построим данный метод для расчета  - значения решения в одном заранее заданном узле. Выберем матрицу переходов
- значения решения в одном заранее заданном узле. Выберем матрицу переходов

Здесь  – символ Кронекера:
– символ Кронекера: 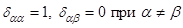 .
.
Далее строим следующую цепь:
1) 
2) если узел  внутренний, то с одинаковой вероятностью ¼ выбираем в качестве
внутренний, то с одинаковой вероятностью ¼ выбираем в качестве  номер одного из соседних с ним узлов;
номер одного из соседних с ним узлов;
3) если узел 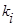 граничный, то цепь останавливается:
граничный, то цепь останавливается:  . Рассчитываем вес вдоль цепи по правилу: пока цепь не попала на границу,
. Рассчитываем вес вдоль цепи по правилу: пока цепь не попала на границу, 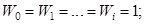 далее
далее  . Вычисляем случайную величину по формуле
. Вычисляем случайную величину по формуле
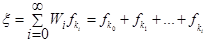 , (8)
, (8)
где – номер первого выхода цепи на границу.
В формуле (6) все 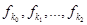 вычисляются по формуле
вычисляются по формуле  и лишь последнее
и лишь последнее  равно значению
равно значению  .
.
Замечание. Если вместо граничных условий (2) заданы более сложные условия, например:
 ,
,
то уравнения (6) наряду с  будут содержать также значения
будут содержать также значения 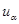 в некоторых узлах. И случайная цепь, попав на границу, останавливаться не будет.
в некоторых узлах. И случайная цепь, попав на границу, останавливаться не будет.
Если количество цепей достаточно велико, то решение задачи Дирихле в узле определяется по формуле
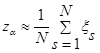 . (9)
. (9)
|
из
5.00
|
Обсуждение в статье: Задача Дирихле для уравнения Пуассона и ее решение методом Монте-Карло с использованием метода сеток |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

