Прикладное применение метода Монте-Карло с использованием метода сеток для решения задачи Дирихле для уравнения Лапласа

Пусть  – решение уравнения Лапласа  в единичном квадрате , удовлетворяющее граничным условиям 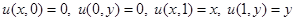. Вычислить значение .

Выберем в квадрате сетку с шагом  и перенумеруем узлы (рис. (4), Приложение Е). Для уравнения Лапласа формула (8) все более упрощается: , так что  равно значению  в том узле, в котором цепь попадает на границу. Возле каждого граничного узла на рис. (4) (Приложение Е) проставлено значение для данного примера.

Для построения цепей необходимо воспользоваться таблицей случайных цифр (таблица 1, Приложение В).

Если случайная цифра  окажется 0 или 4, то будем перемещаться в соседний узел справа, если  окажется 1 или 5, то будем перемещаться влево,  окажется 2 или 6, то перемещаться вверх, если  окажется 3 или 7, то перемещаться вниз; значения , равные 8 или 9, опускаем.

В таблице 2 (Приложение F) приведены 16 случайных цепей. В первой строке записаны использованные случайные цифры, а в третьей – сама цепь (номера ). Соответствующие этим цепям значения  равны . Среднее арифметическое этих величин дает нам приближенное значение решения в точке :

                                                      .

Из эмпирической оценки дисперсии

                                         

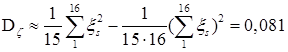
следует, что вероятная ошибка .

Точное решение рассмотренной задачи , так что , и фактическая ошибка расчета равна 0,08.

Приведенный здесь метод позволяет вычислять решения разностных уравнений, аппроксимирующих дифференциальные уравнения.

 

 

Математическое обоснование решения задачи Дирихле для уравнения Пуассона

Найдем решение задачи Дирихле для уравнения Пуассона:

                                                                    ,

где .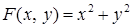

Выберем в квадрате  сетку с шагом . Для построения цепей используем таблицу случайных цифр (таблица 1, Приложение В). Если случайная цифра  окажется 0 или 4, то будем перемещаться в соседний узел справа, если  окажется 1 или 5, то будем перемещаться влево,  окажется 2 или 6, то перемещаться вверх, если  окажется 3 или 7, то перемещаться вниз; значение , равные 8 или 9, опускаем.

Рассчитываем вес вдоль цепи по правилу: пока цепь не попала на границу, далее . Вычисляем случайную величину по формуле

                             ,                                (8)  

где – номер первого выхода цепи на границу.

В формуле (6) все 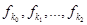 вычисляются по формул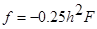е , где , и лишь последнее  равно значению : .

Итоговое значение функции получаем по формуле , где .

Заключение

В данной работе были рассмотрены основные сведения, связанные с задачей Дирихле для уравнений Лапласа и Пуассона – определения, свойства и методы решения. Было приведено два метода решения данной задачи с помощью метода Монте-Карло – метод сеток и метод «блуждания» по сферам для уравнения Лапласа и метод сеток для уравнения Пуассона. Приведено математическое обоснование решения задачи Дирихле для уравнения Пуассона методом Монте-Карло с использованием метода сеток.

В приложении приведена программа, написанная на BorlandPascal 7.0, реализующая данный метод с заданными исходными данными:

                                                                    ,

.

Также приведены рисунки, использованные в работе и таблицы для построения переходов, на основе генерации случайных цифр.

 

Список использованной литературы

1. Соболь И. М. Численные методы Монте-Карло. – М.:Наука, 1973. – 312 с

2. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа. – М.:Наука, 1967. – 368 с.

3. Березин И. С., Жидков Н. П. Методы вычислений. – М.:Государственной литературы, 1959. – 602 с.

4. Бусленко Н. П., Шрейдер Ю. А. Метод статистических испытаний (Монте-Карло) и его реализация в цифровых машинах. – М.:Физматгиз, 1961. – 315 с.

 

Приложения

А. Сеточная область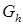  

 

(рис. 1)

 

B. Таблица 1

(блуждание частицы на плоскости)

Случайное число	Характер перемещения
0 или 4	(шаг вправо)
1 » 5	(шаг вверх)
2 » 6	(шаг влево)
3 » 7	(шаг вниз0

 

С. Ограниченная область  

(рис. 2)

D. Ограниченная область 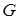 с границей

(рис. 3)

E. Единичный квадрат

(рис. 4)

Единичный квадрат: в нем сетка с шагом , краевые условия:

 

 

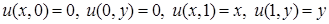
F. Таблица 2

(случайные цепи)

6 5 1 13–18–17–16		5 0 7 5 6 6 1 13–12–13–8–7–12–17–16					5 5 13–12–11
6 6 13–18–23	4 3 4       13–14–9–10				5 6 5 13–12–17–16			5 1 13–12–11
2 3 3 2 4 3 7 13–18–13–8–13–12–17–16				7 5 7            13–8–7–2				0 2 6       13–14–19–24
1 6 0 3 3 3    13–12–17–18–13–8–3					4 2 5 0 2      13–14–19–18–19–8				2 2 13–18–23
4   5     5    5        13–14–13–12–11			3 7 13–18–3			5 1    13–12–11