 |
Главная |
Основные сведения о задаче Дирихле для уравнения Лапласа
|
из
5.00
|
Определение. Функция 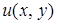 , имеющая непрерывные частные второго порядка в области
, имеющая непрерывные частные второго порядка в области 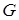 и удовлетворяющая внутри
и удовлетворяющая внутри 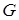 уравнению Лапласа, называется гармонической функцией:
уравнению Лапласа, называется гармонической функцией:
 .
.
Простейшим примером гармонической функции двух переменных является функция вида 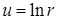 , где
, где  (основное решение уравнения Лапласа).
(основное решение уравнения Лапласа).
Задача Дирихле в иных терминах может быть сформулирована следующим образом: найти функцию, непрерывную в данной замкнутой области 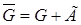 , гармоническую в области и принимающую на ее границе непрерывные заданные значения.
, гармоническую в области и принимающую на ее границе непрерывные заданные значения.
Если  , то задача Дирихле удовлетворяет уравнению Пуассона Единственность решения задачи Дирихле и непрерывная запись ее от краевых условий (корректность краевой задачи) вытекают из следующих гармонических функций.
, то задача Дирихле удовлетворяет уравнению Пуассона Единственность решения задачи Дирихле и непрерывная запись ее от краевых условий (корректность краевой задачи) вытекают из следующих гармонических функций.
Свойcтво1 (принцип максимума). Гармоническая в ограниченной области функция, непрерывная в замкнутой области 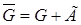 , не может принимать внутри этой области значений больших, чем максимум ее значений на границе
, не может принимать внутри этой области значений больших, чем максимум ее значений на границе  непрерывные заданные значения.
непрерывные заданные значения.
Доказательство. Пусть  – максимум значений
– максимум значений 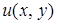 на границе
на границе  . Допустим, что функция
. Допустим, что функция 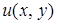 в некоторой точке
в некоторой точке  внутри
внутри 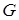 принимает значение
принимает значение  , причем
, причем  .
.
Составим вспомогательную функцию
 ,
,
где 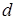 – диаметр области
– диаметр области 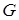 . Очевидно, имеем
. Очевидно, имеем
 ,
,
причем при  выполняется неравенство
выполняется неравенство
 .
.
Следовательно, функция  достигает своего наибольшего значения внутри области
достигает своего наибольшего значения внутри области  в некоторой точке
в некоторой точке  , причем в этой точке будут выполнены необходимые условия для максимума функции:
, причем в этой точке будут выполнены необходимые условия для максимума функции:
 .
.
Из соотношения

вытекает, что по крайней мере одна из производных  или
или  положительна внутри
положительна внутри  . Поэтому функция
. Поэтому функция  ни в какой конкретной точке области
ни в какой конкретной точке области 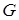 не может иметь максимума, и, следовательно, приходим к противоречию. Таким образом,
не может иметь максимума, и, следовательно, приходим к противоречию. Таким образом,  .
.
Аналогично доказывается, что  , где
, где  – наименьшее значение функции
– наименьшее значение функции  на границе
на границе  .
.
Следствие. Пусть функция  – гармоническая в ограниченной области
– гармоническая в ограниченной области  и непрерывная в замкнутой области
и непрерывная в замкнутой области 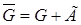 . В таком случае справедливо равенство
. В таком случае справедливо равенство
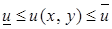 ,
,
где  на
на  ,
,  на
на  .
.
Замечание. Можно доказать более сильное утверждение, что гармоническая в ограниченной и замкнутой области 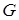 функция, отличная от константы, не принимает внутри
функция, отличная от константы, не принимает внутри 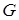 наибольшего и наименьшего значений.
наибольшего и наименьшего значений.
Свойство II (единственность решения задачи Дирихле). Задача Дирихле для замкнутой и ограниченной области может иметь лишь единственное решение, т. е. не существует двух непрерывных гармонических функций в замкнутой ограниченной области 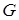 , принимающих, на границе одни и те же значения.
, принимающих, на границе одни и те же значения.
Доказательство. Допустим, что две функции  и
и  гармонические в области
гармонические в области  , совпадают всюду на ее границе. Рассмотрим функцию
, совпадают всюду на ее границе. Рассмотрим функцию
 .
.
Очевидно, что на  – гармоническая функция, обращающаяся в нуль на границе. По свойству I эта функция не может принимать внутри
– гармоническая функция, обращающаяся в нуль на границе. По свойству I эта функция не может принимать внутри 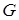 значений больше или меньше нуля, следовательно,
значений больше или меньше нуля, следовательно,  внутри
внутри 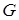 и
и  .
.
Замечание. Из свойства II не следует, что задача Дирихле для ограниченной замкнутой области 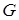 имеет решение; это свойство лишь утверждает, что если существует решение задачи Дирихле для области
имеет решение; это свойство лишь утверждает, что если существует решение задачи Дирихле для области 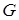 , то оно единственно.
, то оно единственно.
Можно доказать, что если область 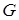 выпуклая, т. е. вместе с двумя своими точками содержит соединяющий их отрезок, и граница ее
выпуклая, т. е. вместе с двумя своими точками содержит соединяющий их отрезок, и граница ее  действительно имеет решение (теорем Неймана).
действительно имеет решение (теорем Неймана).
Свойство III (корректность задачи Дирихле). Решение задачи Дирихле для замкнутой и ограниченной области непрерывно зависит от граничных данных.
Доказательство. Допустим, что  и
и  – решения задачи Дирихле, соответственно принимающее на границе значение
– решения задачи Дирихле, соответственно принимающее на границе значение  и
и  .
.
Пусть всюду на  выполнено неравенство
выполнено неравенство
 ,
,
где  – произвольное малое положительное число.
– произвольное малое положительное число.
Рассмотрим гармоническую функцию
 .
.
На границе  эта функция принимает значение
эта функция принимает значение
 .
.
Так как  на
на  , то по свойству I имеем
, то по свойству I имеем
 при
при  ,
,
т. е.  или
или  .
.
Таким образом, для задачи Дирихле требование корректности выполнено при  .
.
|
из
5.00
|
Обсуждение в статье: Основные сведения о задаче Дирихле для уравнения Лапласа |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

