Основные определения и вспомогательные результаты

Введение

Проективная геометрия исторически возникла в рамках линейной перспективы, которую применяли строители еще в древности (их знания были систематизированы Евклидом в его трактате «Оптика»). Затем, уже в эпоху Возрождения, к ней обратились живописцы, пытавшиеся создавать иллюзию пространства, то есть изображать на плоскости объемные предметы так, как их видит глаз человека.

В проективной геометрии не различают параллельные и пересекающиеся прямые — считают, что параллельные тоже пересекаются, но в бесконечно удаленной, «несобственной» точке; все такие точки, отвечающие разным направлениям прямых на плоскости, образуют несобственную прямую, которую присоединяют к плоскости. Значит, плоскость дополняется несобственной прямой, а трехмерное пространство — плоскостью.

Как и другие геометрии, проективная абсолютно строго задается системой аксиом. В ней фигурируют два типа объектов, называемые «точками» и «прямыми». Важно, что эти аксиомы устанавливают только отношения между объектами, поэтому для них возможны различные интерпретации. В частности, их можно (но совсем необязательно) считать обычными евклидовыми точками и прямыми.

Проективную геометрию можно описывать аналитически и изучать средствами алгебры. При этом вводят так называемые «однородные координаты», которых всегда на одну больше, — именно в них наиболее просто выражаются закономерности этой геометрии. Это не единственный способ координатизации.

Рассмотрим проективную плоскость как аксиоматически заданную инцидентностную структуру, образованную объектами двух видов (точки и прямые). Если количество объектов конечно, то на плоскости можно ввести координаты с использованием элементов некоторого конечного множества. Отношение инцидентности между точками и прямыми позволяет определить на координатизирующем множестве тернарную операцию, а на основе тернара – операции сложения и умножения. Оказывается, геометрические свойства проективной плоскости тесно связаны с алгебраическими свойствами координатизирующего множества, что позволяет классифицировать и исследовать проективные плоскости алгебраическими методами.

Один из интересных классов проективных плоскостей – полуполевые плоскости. Множество, координатизирующее конечную полуполевую плоскость, наиболее близко к полю, координатизирующему классическую, или дезаргову, проективную плоскость.

Известен метод построения полуполевых плоскостей как плоскостей трансляций: на основе векторного пространства и некоторого семейства линейных преобразований, называемого регулярным множеством (spread set).

Наиболее простыми для построения и исследования являются плоскости трансляций ранга 2, регулярное множество которых может быть представлено 2 2-матрицами. Регулярное множество полуполевой плоскости замкнуто по сложению, что упрощает его построение.

Целью работы является построение всех неизоморфных полуполевых плоскостей ранга 2 над полем GF(4) и их исследование.

Первоначально список построенных полуполевых плоскостей порядка 16 содержал 56 объектов, из которого далее были исключены все изоморфные копии.

Изоморфизм полуполевых плоскостей задается полулинейным отображением векторных пространств такого вида: , где σ – автоморфизм поля, А – невырожденная матрица. Так как построен полный набор полуполевых плоскостей данного порядка и ранга, то достаточно рассматривать изоморфизмы вида  или .

На следующем этапе было показано, что изоморфизм  позволяет разбить построенные плоскости на 31 подкласс. Окончательно, было рассмотрено отображение вида  и получено всего 2 неизоморфных полуполевых плоскости порядка 16.

Для каждой из построенных плоскостей была составлена полная система взаимно ортогональных латинских квадратов.

С использованием матричного представления регулярного множества полуполевых плоскостей порядка 16 построены полярности каждой плоскости (анти-автоморфизмы порядка 2). Каждая полярность задана при помощи аддитивного преобразования координатизирующего полуполя. Доказаны некоторые результаты, позволяющие алгоритмизировать процесс поиска таких преобразований. Каждой полярности поставлено в соответствие множество ее абсолютных точек. Дана классификация полученных множеств и соответствующих им полярностей.

 

Основные определения и вспомогательные результаты

 

В данной главе приведены основные определения, используемые в работе, а также некоторые известные факты из теории проективных плоскостей.

 

Основные понятия и определения

Определение 1.1. Проективной плоскостью назовем структуру 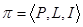, состоящую из двух непустых множеств (множества точек Р и множества прямых L) c отношением инцидентности I между ними таким, что выполняются 3 аксиомы:

1) любые две различные прямые l и m инцидентны единственной точке;

2) любые две различные точки A и B инцидентны единственной прямой;

3) найдутся такие четыре точки, что никакие 3 из них не лежат на одной прямой.

 

Определение 1.2. Порядком проективной плоскости называется такое число n, что:

1) плоскость содержит  точку, столько же прямых;

2) каждая прямая инцидентна с  точками;

3) каждая точка инцидентна с  прямыми.

Определение 1.3. Изоморфизмом проективной плоскости  на проективную плоскость  называется взаимно однозначное отображение точек  в точки , прямых  – в прямые , сохраняющее отношение инцидентности.  

 

Определение 1.4. Автоморфизм (коллинеация) проективной плоскости – изоморфизм плоскости на себя.

 

Определение 1.5. Анти-изоморфизмом проективной плоскости  на проективную плоскость  называется взаимно однозначное отображение точек  в прямые , прямых  – в точки , инвертирующее отношение инцидентности.  

 

Определение 1.6. Корреляция  – анти-изоморфизм плоскости на себя.

 

Определение 1.7. Корреляция γ называется полярностью, если γ²=1.

Определение 1.8. Трансляционной прямой l плоскости π называется такая прямая, что для любых двух точек А и В, не лежащих на этой прямой, найдется автоморфизм β  плоскости π , который переводит А в В и фиксирует прямую l поточечно.

 

Определение 1.9. Трансляционной точкой К плоскости π называется такая точка, что для любых двух различных точек А и В, лежащих с К на одной прямой, но отличных от нее, найдется автоморфизм β плоскости π , который переводит А в В и фиксирует все прямые, проходящие через К,  не поточечно.

 

Определение 1.10. Проективная плоскость π является плоскостью трансляций, если она содержит трансляционную прямую.

 

Определение 1.11. Проективная плоскость, содержащая трансляционную прямую и трансляционную точку, называется полуполевой плоскостью.

 

1.2. Координатизация  проективной плоскости

Пусть Р – конечная проективная плоскость, 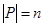, т.е. Р содержит  точку и столько же прямых. Пусть D – такое множество, состоящее из  символов, что , 0 ≠ 1, ∞ .

С помощью D введем координаты для всех точек и прямых проективной плоскости Р.

Выберем 4 точки, образующие невырожденный четырехугольник: O, X, Y, I (рис. 1):

 

                                                     Y

                                                                                                                                                

                     

                                                                               I'                                                                                       

                                                                    

                                                                I

 

                                                                              

                                                     А                                  F

                                                                                                                      

       O                                                                                          X         

                    

                                                         

Рис. 1

 

Рассмотрим точки прямых и сопоставим им элементы либо пары элементов множества D.

Точки прямой OI, кроме точки I'.

Каждой точке поставим в соответствие элемент из D: 

O  0 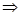 O=(0,0),

A  a  A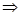=(a,a),

I  1.

Точки прямой OX=[0,0], кроме точки X.

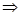 D= (d,0).

Точки прямой OY=[0], кроме точки Y.

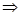 С=(0,с).

Точки, не лежащие на прямых OI, OX, OY.

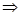  F=(f, g),

.

Точки прямой XY=[∞].

,  

Y=(∞),

X=(0).

Прямые.

 

Таким образом, мы получили плоскость, где каждая точка и прямая имеет свои координаты (рис. 2).

             (∞)

     

         [ b]

      [0]                                    ( m)

                                                                      ( b, y)

                                                                           

                                                                  [ m, k]                                    

                                     (0, k)

                                                                    ( b,0)       [0,0]                          (0)

                              

                        (0,0)                                                                                        [∞]

                                                                                                                  

Рис. 2

Определим на множестве D тернарную операцию T:  точка  инцидентна прямой . Далее введем бинарные операции сложения и умножения следующим образом:

· ,

· .

 

Определение 1.12. Непустое множество G с заданной на нем бинарной операцией * называется лупой, если выполняются аксиомы:

1) для любых   существует единственный элемент 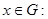 a* x= b;

2) для любых   существует единственный элемент  y* a= b;

3) существует  для любого элемента   e* x= x* e= x.

 

 

Определение 1.13. Непустое множество Q с заданными на нем бинарными операциями + и  является квазиполем, если:

1)  – группа;

2)  – лупа;

3)   x*(y+ z)= x* y+ x* z (левая дистрибутивность);

4)   0* x=0;

5) уравнение a* x= b* x+ c имеет единственное решение x для 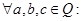 а≠ b.

 

Определение 1.14. Квазиполе с правой дистрибутивностью называется полуполем (или кольцом с делением).

 

Известен результат [1], что проективная плоскость кординатизируется полуполем тогда и только тогда, когда  – трансляционная прямая и 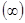 – трансляционная точка.