Изоморфизм полуполевых плоскостей

На следующем этапе работы было необходимо разбить множество построенных плоскостей на классы плоскостей, изоморфных между собой. Для этой цели была применена теорема, доказанная в [3].

Теорема 2.2. Пусть π – спрэд V, π' – спрэд V'. Если σ – изоморфизм плоскости трансляций π(V) на плоскость трансляций π'(V') такой, что 0^σ =0, тогда σ – биективное полулинейное отображение векторного пространства V на векторное пространство V' .

 

Или другими словами, плоскость π изоморфна плоскости π΄  найдется полулинейное отображение , сохраняющее компоненты расщепления,

.

Здесь σ – автоморфизм поля GF(4), А – невырожденная матрица, (x, xθ) π, а .

 

Установление изоморфизма заключается в определении зависимости между матрицами регулярных множеств (а точнее, между функциями, определяющими вид матриц).

Возможны случаи:

I) А=Е, σ – возведение в квадрат;

II) А 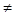Е, σ=1;

 III) А 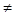Е, σ – возведение в квадрат. 

Так как мы рассматриваем полный список плоскостей, то достаточно установить наличие изоморфизмов типа I и II.

Рассмотрим случай I.

Пусть    , а .

Известно:

.

Зная, что х= , , получаем:        

,

.

Таким образом, мы получили, что , т.е. все коэффициенты, стоящие при переменных u и v, возводятся в квадрат:

,

.

 

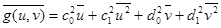Рассмотрев первую плоскость, мы найдем изоморфную ей:

первая плоскость изоморфна второй (1 2);

Дальнейшие вычисления показывают, что: (3 3), (4 4), (5 5), (6 6), (7 11), (8 12), (9 13), (10 14), (15 15), (16 16), (17 18), (19 20), (21 22), (23 24), (25 27), (26 28), (29 43), (30 44), (31 45), (32 46), (33 47), (34 48), (35 55), (36 56), (37 50), (38 49), (39 52), (40 51), (41 53), (42 54).

 

Итак, построив отображение типа I (А=Е, σ: ), мы получили 31 класс плоскостей, все плоскости приведены в приложении 2. Далее мы работали с этими классами.

 

 

Рассмотрим случай II.

Для любой матрицы  существует матрица   

,

здесь А _i – матрицы размерности 2 2 над GF(4).

Рассмотрим изоморфные полуполевые плоскости.

                                                                        (∞)

 

                                                                  [0]

 

                                                         (0, y)                                [∞]

 

 

                                              (0,0)

 

Рис. 3

 

Все точки, находящиеся на прямой [0] первой плоскости, имеют вид (0,у). Под действием изоморфного отображения они должны перейти в точки, лежащие на прямой [0] второй плоскости (так как точка (0,0) фиксируется и точка (∞)– трансляционная) (рис. 3). Следовательно,

.

Таким образом, мы имеем:

,

и .

Из последнего равенства получим:

.

Для θ = 0 имеем:

, .

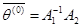Следовательно,

,

,

.

Т.к. регулярное множество замкнуто по сложению, то можно сделать замену:

.

Таким образом, мы получаем:

                                                               .                                      

Для θ = Е имеем  

, .

Для  имеем .

Рассмотрим подробнее получившуюся матрицу А:

.

Заметим, что S – изоморфизм :

,

это преобразование – элация с осью [0] и центром (∞). Можно сделать вывод, что достаточно рассматривать изоморфизмы вида

,

где А₄– любая невырожденная матрица с элементами из GF(4),  – некоторая из R.

Тогда

,

 

Таким образом, для любой  существует : , то есть регулярное множество  второй плоскости сопряжено с множеством  для некоторой матрицы .

 

Этот результат уточняет теорему, приведенную в [2].

 

Теорема 2.3.Плоскости трансляций Г' и Г изоморфны тогда и только тогда, когда R' сопряжено в GL(V) с одним из следующих множеств:

1) , где l ≠ k;

2) , где l ≠ r;

3) , где l, k, r – попарно различные элементы V;

4) , где k ≠ r.

В этой теореме выражение вида 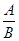 означает .

Наш результат справедлив для линейных изоморфизмов полуполевых плоскостей.

 

Теорема 2.4. Если φ – линейный изоморфизм полуполевых плоскостей, то он может быть задан матрицей вида , где А₄ – любая невырожденная матрица с элементами из GF(4), ≠ 0 – некоторая матрица из R .

Следует заметить, что в случае поля четного порядкадостаточно рассматривать матрицу  с определителем равным 1. Покажем, что это действительно так.

 

Пусть матрица имеет вид:

A=  и .

Тогда матрицу А можно записать в таком виде:

A= , и |A|= ,

.

(т.к. в поле четного порядка квадратный корень из любого элемента извлекается однозначно, то мы имеем право сокращать).

 

Была написана программа на языке С++, рассчитывающая данный случай. В итоге мы получили 2 класса неизоморфных полуполевых плоскостей порядка 16:

I) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56}

II) {17, 18, 31, 32, 45, 46}

или всего 2 плоскости: №1 и №17, и 17-я плоскость является дезарговой.Обозначим эти плоскости   и  соответственно.

 

Для плоскостей номер 1 и 17 матрицы имеют вид:

 и .

 

Лемма 2.5. Для дезарговой плоскости (плоскость №17) регулярное множество является полем.

Доказательство леммы 2.5. Функции матрицы регулярного множества для плоскости №17 имеют вид:

, .

Проверим необходимые аксиомы:

1) Замкнутость по умножению:

,

.

Замкнутость выполняется.

 

2) Коммутативность умножения:

,

,

Коммутативность выполняется.

 

3) Ассоциативность умножения:

,

 

Преобразуем левую часть равенства:

.

Преобразуем правую часть равенства:

 

.

Ассоциативность выполняется.

4) Наличие обратного элемента:

.

Лемма 2.5 доказана.