 |
Главная |
Тема 1. Прогнозирование с учетом сезонной составляющей
|
из
5.00
|
Институт экономики и управления
Кафедра Экономическая кибернетика
Методические указания по лабораторным работам
По дисциплине Методы социально-экономического прогнозирования
Для специальности
080116.65 «Математические методы в экономике»
Методические указания разработаны в соответствии с составом УМКД
Методические указания разработала Порошина Л.А. _____________
Методические указания утверждены на заседании кафедры,
протокол № ______ от «___» _______________ 200__ г.
Зав. кафедрой _________ «___» ______________ 200__ г. Пазюк К.Т.
Методические указания по лабораторным работам по дисциплине «Эконометрическое моделирование» включают тематику лабораторных заданий, выполняемых во время аудиторных занятий.
Методические указания рассмотрены и утверждены на заседании УМКС и рекомендованы к изданию
протокол № ______ от «___» _______________ 200__ г.
Председатель УМКС _______ «___» __________ 200__ г.
Директор института _________ «___» ____________ 200__ г. Зубарев А.Е.
Введение
Реалии нынешнего этапа развития российской государственности выдвигают в число первоочередных задачу перехода к стабильному, предсказуемому и эффективному развитию экономики страны, что в свою очередь не возможно без специальных знаний в области методологии, методики и технологии составления научно-обоснованных макро- и микроэкономических прогнозов социально-экономического развития. Масштаб стоящих перед российским бизнесом проблем, а также качественный уровень развития современного научно-технического потенциала требует соответствующей теоретической и практической подготовки специалистов в области экономико-математического моделирования. Прогнозная информация, с одной стороны, необходима как основа планирования деятельности любого социально-экономического объекта, а с другой стороны - как предварительная оценка последствий принимаемых решений с целью их оптимизации. Отсюда ясна важность данной дисциплины для формирования специалиста в области математических методов и исследования операций в экономике.
В этой связи цель дисциплины "Методы социально-экономического прогнозирования" - вооружить студентов специальности "Математические методы в экономике" - 080116.65 знаниями общих закономерностей составления научных прогнозов развития социально-экономических объектов; познакомить их с максимально широким инструментарием выработки прогнозов развития социально-экономических объектов, а также методиками его использования в практике прогнозирования; выработать в процессе обучения у студентов навыки грамотного использования аппарата математического моделирования посредством применения передовых информационных технологий.
Задачи курса: изучение методологических основ прогнозирования, а также приемов и методов прогнозирования экономических процессов.
Дисциплина «Методы социально-экономического прогнозирования» опирается на материал учебных дисциплин: «Математический анализ», «Теория вероятности и математическая статистика», «Экономическое моделирование», «Математические методы исследования операций», «Эконометрика» и других дисциплин. В соответствии с Государственным образовательным стандартом она является дисциплиной специализации по специальности «Математические методы в экономике» и полностью соответствует по содержанию его требованиям.
Основная цель лабораторных занятий - углубленное изучение проблем, затронутых в лекционном курсе, и отработка навыков в применении изучаемых методов и процедур прогнозирования с использованием современного программного обеспечения персональных компьютеров.
В качестве базового информационно-программного инструментария на лабораторных работах предлагается воспользоваться продуктами Excel, StatGraphics, Statistica. В ходе освоения дисциплины студенты могут ознакомиться и с дополнительными программными средами, например, Matlab (Statistics Toolbox, GARCH Toolbox), Mathcad, SPSS, Eviews и др., а также специальными оптимизационными и модулями математических пакетов Matlab (Optimization Toolbox), Mathcad, Mathematica и др.
Изучение дисциплины заканчивается написанием и защитой курсовой работы и сдачей итогового экзамена.
Краткие характеристики лабораторных работ
Тема 1. Прогнозирование с учетом сезонной составляющей
Задание. Построить точечный и интервальный прогноз на основе мультипликативной модели, аддитивной модели и модели Винторса.
Исполнение: выполнение индивидуального задания с использованием Excel. Интерпретация результатов решения.
Оценка. Практическая реализация теоретических методов прогнозирования.
Время выполнения заданий: 2 часа.
Методические указания
Построение аддитивной модели временного ряда. Обратимся к данным об объеме правонарушений на таможне за четыре года, представленным в табл. 1.
Было показано, что данный временной ряд содержит сезонные колебания периодичностью 4, т.к. количество правонарушений в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 1).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 1).
Таблица 1 – Расчёт сезонной компоненты
№ квартала,
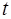
| Количество правонарушений,

| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 375 | – | – | – | – |
| 2 | 371 | 2630 | 657,5 | – | – |
| 3 | 869 | 2612 | 653 | 655,25 | 213,75 |
| 4 | 1015 | 2712 | 678 | 665,5 | 349,5 |
| 5 | 357 | 2835 | 708,75 | 693,75 | -336,75 |
| 6 | 471 | 2840 | 710 | 709,375 | -238,375 |
| 7 | 992 | 2873 | 718,25 | 714,125 | 277,875 |
| 8 | 1020 | 2757 | 689,25 | 703,75 | 316,25 |
| 9 | 390 | 2757 | 689,25 | 689,25 | -299,25 |
| 10 | 355 | 2642 | 660,5 | 674,875 | -319,875 |
| 11 | 992 | 2713 | 678,25 | 669,375 | 322,625 |
| 12 | 905 | 2812 | 703 | 690,625 | 214,375 |
| 13 | 461 | 2740 | 685 | 694 | -233 |
| 14 | 454 | 2762 | 690,5 | 687,75 | -233,75 |
| 15 | 920 | – | – | – | – |
| 16 | 927 | – | – | – | – |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 1). Используем эти оценки для расчета значений сезонной компоненты  (табл. 2). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты
(табл. 2). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты  . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 2 – Расчёт скорректированной сезонной компоненты
Показатели
Год
№ квартала, 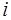
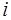 -й квартал
-й квартал
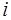 -го квартала,
-го квартала, 



 .
. .
. ) и заносим полученные данные в таблицу 2.
) и заносим полученные данные в таблицу 2. .
. (гр. 4 табл. 3). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
(гр. 4 табл. 3). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

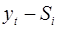
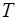


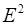
 данной модели. Для этого проведем аналитическое выравнивание ряда (
данной модели. Для этого проведем аналитическое выравнивание ряда (  ) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
) с помощью линейного тренда. Результаты аналитического выравнивания следующие: .
.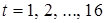 , найдем уровни
, найдем уровни 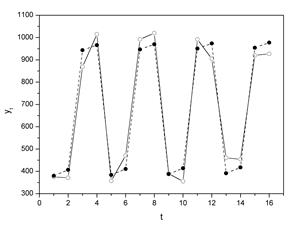

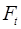 уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда .
.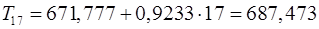 ;
; .
. и
и  . Таким образом,
. Таким образом, ;
; .
.