Упражнения для самостоятельной работы

Исходя из определения, исследовать на устойчивость нулевые равновесия следующих дифференциальных уравнений

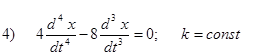
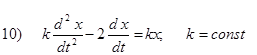
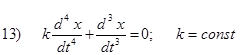
Первый метод Ляпунова

В своей первой методе Ляпунов поставил и разрешил вопрос, когда линеаризованные уравнения полностью разрешают задачу об устойчивости и неустойчивости. Рассмотрим этот метод на примере автономной системы вида

Пусть x=a - некоторое равновесие системы, то есть f(a)=0. Введем возмущения

x(t)=a+y(t)

и перейдем к уравнению возмущений

Исследуем на устойчивость нулевое равновесие уравнения возмущений. Для этого линеаризуем уравнение (11), раскладывая функцию f в ряд Тейлора в точке y=0

Переход от уравнения (11) к линейному уравнению (12) называется линеаризацией. Идея первого метода Ляпунова заключается в исследовании на устойчивость равновесий линеаризованного уравнения. 

Первая теорема Ляпунова о законности линеаризации. Если нулевое равновесие линеаризованного уравнения (12) асимптотически устойчиво, то и нулевое равновесие нелинейного уравнения (11) - асимптотически устойчиво.

Вторая теорема Ляпунова о законности линеаризации. Если среди собственных чисел линеаризованного уравнения (12) есть хотя бы одно, вещественная часть которого больше нуля, то нулевое равновесие нелинейной системы (11) неустойчиво.

Две сформулированные теоремы не дают ответа на вопрос, что будет, если одно из собственных чисел линеаризованного уравнения лежит на мнимой оси (его вещественная часть равна нулю), а все остальные собственные числа лежат в левой полуплоскости. Такой случай называется критическим. В критическом случае ответ на вопрос об устойчивости нельзя получить без учета нелинейных слагаемых, и необходимо использовать другие методы для исследования устойчивости.

    При использовании первого метода Ляпунова в конечномерном случае часто используется следующее утверждение.

Утверждение. Если все собственные числа линейного уравнения (12) лежат в левой полуплоскости (их вещественные части строго меньше нуля), то нулевое равновесие линейного уравнения асимптотически устойчиво. Если среди собственных чисел линейного уравнения (12) есть хотя бы одно, вещественная часть которого строго больше нуля, то нулевое равновесие уравнения (12) неустойчиво.

Пример 1. Исследовать первым методом Ляпунова устойчивость всех равновесий системы

Для нахождения равновесий решим конечную систему вида

Имеем четыре равновесия:

(x=0; y=5),    (x=0; y=-5),  (x=5; y=0),      (x=-5; y=0)

Исследуем на устойчивость первое равновесие - (x=0; y=5).  Для этого перейдем в (13) к возмущениям

                                       u=x; v=5+y

Уравнение возмущений примет вид

Линеаризуем уравнение возмущений (14), получим

Для нахождения собственных чисел линеаризованной системы λ_i решим уравнение

               |A - λ_i E | =0                                                                                (15)

где А - матрица линеаризованного уравнения возмущений, Е - единичная матрица. Уравнение (15) примет вид

Отсюда,

Следовательно, равновесие (x=0; y=5) - неустойчиво.

Исследуем на устойчивость второе равновесие - (x=0; y=-5).  Для этого перейдем в (13) к возмущениям

                                       u=x; v=-5+y

Уравнение возмущений примет вид

Линеаризуя уравнение возмущений, получим

Характеристическое уравнение примет вид

Отсюда, как и в предыдущем случае получим, что

Следовательно, равновесие (x=0; y=-5) - неустойчиво.

Для третьего равновесия (x=5; y=0), переходя к возмущениям

                                       u=5+x; v=y

получим систему

Линеаризуя, имеем

Характеристическое уравнение примет вид

то есть

Равновесие (x=5; y=0) - неустойчиво.

В случае (x=-5; y=0), переходя к возмущениям

                                       u=-5+x; v=y

получим систему

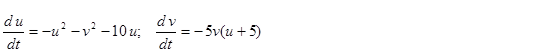
Линеаризуем

Характеристическое уравнение примет вид

Равновесие (x=-5; y=0) – асимптотически устойчиво по Ляпунову.

    Отметим, что в этом примере первый метод Ляпунова позволил полностью решить задачу об устойчивости или неустойчивости по Ляпунову равновесий системы дифференциальных уравнений. В общем случае, это не всегда так. В критическом случае ответ на вопрос об устойчивости дает второй метод Ляпунова.