Упражнения для самостоятельной работы

Исследовать на устойчивость первым методом Ляпунова все равновесия систем

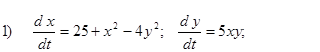
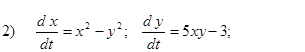
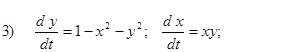
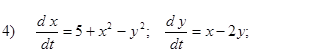
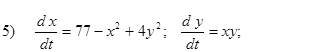
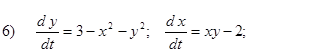
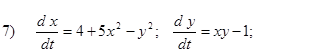
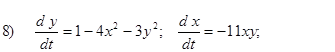
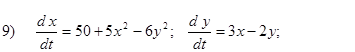
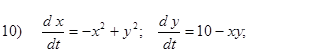
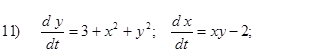
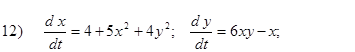
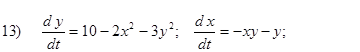
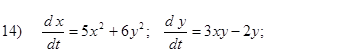
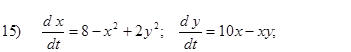
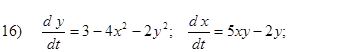
- Исследовать на устойчивость первым методом Ляпунова все равновесия следующих систем в зависимости от вещественного параметра k

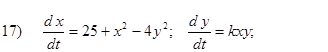
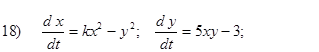
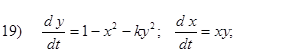
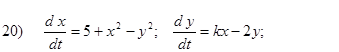
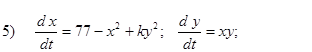
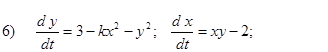
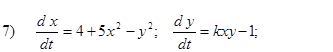
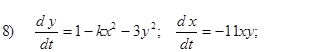
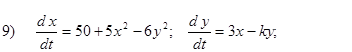
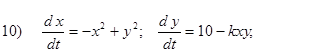
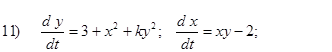
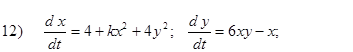
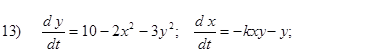
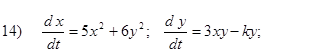
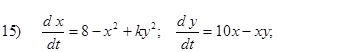
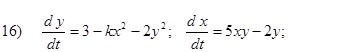
Второй метод Ляпунова

Исследуем на устойчивость нулевое равновесие уравнения возмущений (2). Развитый Ляпуновым прямой метод (вторая метода Ляпунова) изучения устойчивости состоит в отыскании функций переменных (t,x), полные производные которых по времени в силу уравнения (2) обладают некоторыми свойствами.

Рассмотрим функцию V(x,t), которая непрерывно дифференцируема по t и по x=(x₁,x₂,...,x_n). Пусть x^* - некоторое решение дифференциального уравнения (2). Найдем полную производную функции V по времени t на решении x^*.

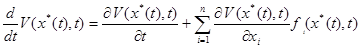
Производной функции V(x,t) в силу дифференциального уравнения (2) назовем величину

                         

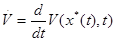
Определение. Функция V(x,t), определенная в полуцилиндре D_0,r={ (x,t): t>0; |x|<r; r>0; }, называется функцией Ляпунова, если V(0,t)=0 и V'(x,t) - знакопостоянна (либо меньше нуля, либо больше нуля, либо тождественно равна нулю).

Определение. Пусть функция W(x) не зависит от времени t, W(0)=0, и знакопостоянна. Для определенности пусть функция W(x) - знакоположительна. Будем говорить, что функция W положительно определенна (отрицательно определенна) , если W(x)>0 (W(x)<0) и W(x)=0 тогда и только тогда, когда x=0.

Определение. Функция V(x,t), определенная в полуцилиндре D_0,r, называется определенно положительной, если V(0)=0, и существует не зависящая от t определенно положительная функция W(x) такая, что для всех точек (x,t) из D_0,r; r>0 выполнено неравенство V(x,t) ≥ W(x).

Если в качестве функции Ляпунова берется квадратичная форма, то вопрос о ее положительной определенности решается с помощью критерия Сильвестра.

Критерий Сильвестра. Квадратичная форма положительно определенна, если все главные миноры матрицы, отвечающей квадратичной форме, строго больше нуля.

Теорема Ляпунова об устойчивости. Пусть для данного уравнения возмущений (2) существует определенно положительная функция Ляпунова, производная которой в силу заданного дифференциального уравнения знакоотрицательна. Тогда нулевое равновесие уравнения возмущений устойчиво по Ляпунову.

Функция Ляпунова, о которой идет речь в теореме называется функцией Ляпунова первого рода.

Определение. Рассмотрим функцию V(x,t), определенную в полуцилиндре D_0,r и такую, что V(0,t)=0. Говорят, что функция V(x,t) допускает бесконечно малый высший предел при x → 0, (V(x,t) → 0 при x → 0), если для любого числа ε>0 существует число δ >0 такое, что из неравенства ||x||<δ следует неравенство |V(x,t)|<ε для всех t>0.

Теорема Ляпунова об асимптотической устойчивости. Пусть для данного уравнения возмущений (2) существует положительно определенная функция Ляпунова, допускающая бесконечно малый высший предел при x → 0, и ее производная в силу дифференциального уравнения отрицательно определенна, тогда нулевое равновесие асимптотически устойчиво.

Функция Ляпунова, о которой идет речь в теореме называется функцией

Ляпунова второго рода.

Для обнаружения неустойчивости невозмущенного движения, достаточно указать всего одну траекторию, выходящую за заданную область, при сколь угодно малых возмущениях.

Теорема Ляпунова о неустойчивости. Пусть для данного уравнения возмущений (2) (функция f(x,t) - непрерывна по переменной t и непрерывно дифференцируема по переменной x) существует функция Ляпунова V(x,t), допускающая бесконечно малый высший предел при x → 0, и обладающая знакоопределенной производной в силу дифференциального уравнения V'(x,t). Если в любой достаточно малой окрестности нуля пространства Rⁿ при некотором значении t₀, большем нуля найдется точка (t₀,x₀), для которой знак функции Ляпунова совпадает со знаком производной в силу дифференциального уравнения, 

                               V(t₀,x₀) V'(t₀,x₀) >0,

То нулевое равновесие уравнения (2) неустойчиво по Ляпунову.

Функция Ляпунова, удовлетворяющая теореме Ляпунова о неустойчивости, называется функцией Ляпунова третьего рода.

Пример 1. Исследовать на устойчивость вторым методом Ляпунова все равновесия системы при различных значениях параметров a, b

Найдем равновесия из решения системы

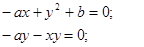
Отсюда, если a≠0, то имеется равновесие (x=b/a; y=0). Если b<-a², то есть равновесия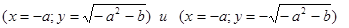

Исследуем устойчивость равновесия (x=b/a; y=0) вторым методом Ляпунова. Перейдем к возмущениям

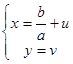
и уравнению возмущений

Умножим первое уравнение на u, второе – на v. Сложим два получающихся уравнения, после преобразований получим

К выбору функции Ляпунова следует подходить творчески, в данном вопросе нет общепринятого подхода. В данном примере в качестве функции Ляпунова логично попробовать взять кинетическую энергию системы, потому что в левой части последнего равенства стоит знакоотрицательная функция. Итак, в качестве функции Ляпунова возьмем

                                    

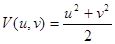
Ясно, что таким образом выбранная функция Ляпунова является положительно определенной функцией. Эта функция удовлетворяет всем требованиям теоремы Ляпунова об устойчивости в случае, когда определяемая формулой (17) производная функции Ляпунова в силу дифференциального уравнения (16) является знакоотрицательной. Последнее условие будет выполнено в случае, когда

             a+b/a>0

В этом случае равновесие (x=b/a; y=0) является устойчивым.

На устойчивость по Ляпунову остальные равновесия исследуйте самостоятельно.

Пример 2. Колебание маятника с трением.

Рассмотрим уравнение

где постоянная h играет роль коэффициента силы трения. Уравнение (17) описывает колебания маятника в среде с трением.

Исследуем на устойчивость нулевое равновесие уравнения (17) (очевидно, что оно существует). Найдем полную энергию системы (то есть интеграл системы (17)) и возьмем ее в качестве искомой функции Ляпунова второго рода

     

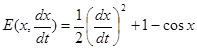
Производная функции E в силу дифференциального уравнения (17) имеет вид

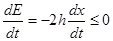
Проверить самостоятельно, что функция E является функцией Ляпунова первого рода и, следовательно, нулевое равновесие уравнения (17) устойчиво по Ляпунову.

Попробуем построить функцию Ляпунова второго рода, то есть доказать асимптотическую устойчивость нулевого равновесия уравнения (17). Функцию Ляпунова второго рода будем разыскивать в виде

Здесь α₁, α₂ - произвольные постоянные, подлежащие определению.

Потребуем, чтобы функция (18) удовлетворяла всем требованиям второй теоремы Ляпунова. Из этих требований получим систему неравенств, из которой определяются постоянные α₁, α₂. Если удастся найти хотя бы один набор этих постоянных, позволяющий удовлетворить условия теоремы Ляпунова об асимптотической устойчивости, то нулевое равновесие уравнения (18) будет асимптотически устойчиво, в противном случае надо разыскивать функцию Ляпунова в другом виде.

Проверить самостоятельно, что в данном случае нулевое равновесие асимптотически устойчиво и постоянные α₁, α₂, например, определяются равенствами

α₁= h/2;  α₂=h²/2

Для проверки воспользуйтесь критерием Сильвестра. Выпишите соответствующие определители и найдите одно из решений возникающих неравенств. Постоянные α₁ и α₂ определяются неединственным образом.