 |
Главная |
Неподвижные точки различных видов движений пространства.
|
из
5.00
|
Найдём множества неподвижных точек различных видов движений:
1. Тождественное преобразование. Множеством неподвижных точек тождественного преобразования является всё пространство.
2. Параллельный перенос. Если  , то
, то  - тождественное преобразование и неподвижными будут все точки пространства. Если
- тождественное преобразование и неподвижными будут все точки пространства. Если 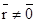 , то у
, то у  нет неподвижных точек.
нет неподвижных точек.
3. Поворот вокруг оси, осевая симметрия. Если угол поворота равен 2πk (  ), то он является тождественным преобразованием. Тогда неподвижны все точки. Если угол поворота не равен 2πk (
), то он является тождественным преобразованием. Тогда неподвижны все точки. Если угол поворота не равен 2πk (  ) (в частности, если он является осевой симметрией), то множеством неподвижных точек является ось симметрии.
) (в частности, если он является осевой симметрией), то множеством неподвижных точек является ось симметрии.
4. Центральная симметрия. Неподвижной точкой является только центр симметрии.
5. Зеркальная симметрия. Неподвижными точками являются точки плоскости симметрии.
6. Переносная симметрия, поворотная симметрия, винтовое движение.
· У переносной симметрии неподвижных точек нет
· У винтового движения неподвижных точек нет.
· У поворотной симметрии  единственная неподвижная точка
единственная неподвижная точка 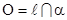 .
.
Наглядно вывод можно представить в виде следующей таблицы (для всех преобразований мы не берём в расчёт их частный случай, когда они являются тождественными):

Впоследствии мы докажем, что движения пространства ограничиваются перечисленными в таблице. Поэтому наша таблица полная.
Теперь докажем несколько теорем, которые нам понадобятся в дальнейшем.
Теорема 4.1. (признак поворота) Если множеством неподвижных точек движения является прямая ℓ, то это движение – поворот около прямой ℓ.
Доказательство. Из аналогичной теоремы на плоскости следует, что в каждой плоскости, перпендикулярной ℓ, происходит поворот. Все эти повороты происходят на один и тот же угол, т.к. каждая плоскость, содержащая ℓ, как легко показать, при нашем движении переходит в плоскость, также содержащую ℓ. Значит, наше движение – поворот около ℓ.
Теорема 4.2. (признак зеркальной симметрии) Если множеством неподвижных точек движения является плоскость α, то это движение – симметрия относительно плоскости α.
Доказательство. Пусть α – плоскость неподвижных точек, Х – произвольная точка пространства, не лежащая в α. Опустим перпендикуляр ℓ из Х на α. Прямая ℓ при нашем движении переходит в себя, так как она остаётся перпендикулярной плоскости α и проходит через ту же точку (назовём её О) плоскости α (потому что эта точка неподвижна). Тогда Х´, образ точки Х при нашем движении, лежит на прямой ℓ. При этом ОХ´=ОХ, т.е. Х´ симметрична Х относительно плоскости α. Таким образом, наше движение – симметрия относительно плоскости α.
|
из
5.00
|
Обсуждение в статье: Неподвижные точки различных видов движений пространства. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

