Проективные преобразования плоскости.

Определение. Проективная плоскость – обычная (евклидова)плоскость, дополненная бесконечно удаленными точками и бесконечно удаленной прямой, называемыми также несобственными элементами. При этом каждая прямая дополняется одной несобственной точкой, вся плоскость – одной несобственной прямой; параллельные прямые дополняются общей несобственной точкой, непараллельные – разными; несобственные точки, дополняющие всевозможные прямые плоскости, принадлежат несобственной прямой.

 

Определение. Преобразование проективной плоскости, переводящее любую прямую в прямую, называется проективным.

 

Следствие. Проективное преобразование, сохраняющее бесконечно удалённую прямую является аффинным; любое аффинное преобразование является проективным, сохраняющим бесконечно удалённую прямую.

 

Определение. Центральным проектированием плоскости α на плоскость β с центром в точке О, не лежащей на этих плоскостях, называется отображение, которое любой точке А плоскости α ставит в соответствие точку А´ пересечения прямой ОА с плоскостью β.

При этом, если плоскости α и β не параллельны, то в плоскости α найдётся прямая ℓ такая, что плоскость, проходящая через точку О и прямую ℓ, параллельна плоскости β. Будем считать, что ℓ при нашем проектировании переходит в бесконечно удалённую прямую плоскости β (при этом каждая точка B прямой ℓ переходит в ту точку бесконечно удалённой прямой, что дополняет прямые параллельные ОВ). В плоскости β найдётся прямая ℓ´ такая, что плоскость, проходящая через точку О и прямую ℓ´, параллельна плоскости α. Будем считать ℓ´ образом бесконечно удалённой прямой плоскости α. Прямые ℓ и ℓ´ будем называть выделенными.

Мы можем говорить, что задано просто преобразование проективной плоскости (если совместить плоскости α и β).

 

Из определения сразу вытекают свойства центральной проекции:

1. Центральное проектирование – проективное преобразование.

2. Обратное к центральному проектированию преобразование – центральное проектирование с тем же центром.

3. Прямые, параллельные выделенным, переходят в параллельные.

 

Определение. Пусть точки А, В, С, D лежат на одной прямой. Двойным отношением (АВ; СD) этих точек называется величина 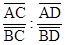. Если одна из точек является бесконечно удалённой, то длины отрезков, концом которых является эта точка, можно сократить.

 

Теорема 1.1. Центральная проекция сохраняет двойные отношения.

 

Доказательство. Пусть О – центр проектирования, А, В, С, D – четыре точки, лежащие на одной прямой, A´, B´, C´, D´ – их образы.

 Тогда .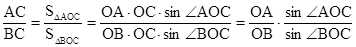

 Аналогично .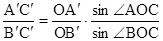

 Поделив одно равенство на другое, получим .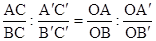

Аналогично, вместо точки С рассматривая точку D, получим .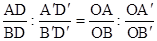

Отсюда 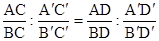, т.е. .

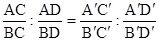Чтобы доказательство было полным, осталось заметить, что все отрезки, площади и углы можно считать ориентированными.

 

Теорема 1.2. Пусть даны четыре точки A, B, C, D плоскости π, не лежащие на одной прямой, и четыре точки M, N, P, Q плоскости π´, не лежащие на одной прямой. Тогда существует композиция центральной (параллельной) проекции и подобия, переводящая A в M, В в N, С в Р, D в Q.

 

Доказательство.

Будем для удобства говорить, что ABCD и MNPQ – четырёхугольники, хотя на самом деле это не обязательно (например, могут пересекаться отрезки АВ и CD). Из доказательства будет видно, что мы нигде не используем, что точки A, В, С, D и M, N, P, Q в указанном порядке образуют четырёхугольники.  

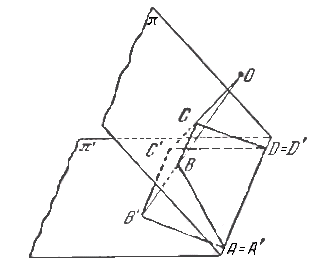
I. Если наши четырёхугольники – трапеции (АD||BC и MQ||NP), то доказательство совсем простое. Рассмотрим четырёхугольник A´B´C´D´, подобный четырёхугольнику MNPQ, такой, что AD=A´D´. Расположим плоскости π и π´ так, чтобы совпали точки А с А´ и D с D´. Теперь, если 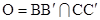, то нужный нам результат даст центральная проекция с центром О (см. рис.), а если ВВ´||CC´, то нужный нам результат даст параллельная проекция с направлением ВВ´.

II. Теперь докажем утверждение, если четырёхугольники произвольные. Пусть 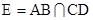, 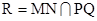. Отметим точки Х₁, Х₂, Z₁, Z₂ на прямых АВ, CD, MN, PQ соответственно так, что

; ; ; .

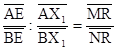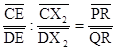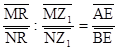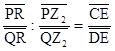Проведём теперь через точки A, B, C, D прямые АK, BL, CF, DG, параллельные X₁X₂ (K, L лежат на DC; G, F – на АВ), а через точки N, M – прямые NT, MS, параллельные Y₁Y₂ (T, S лежат на PQ). Переведём центральной (параллельной) проекцией f трапецию АВLK в трапецию А´В´L´K´ плоскости π´, подобную трапеции MNTS (это возможно по части I нашего доказательства). При этом из выбора точек Х₁, Х₂ следует, что прямая Х₁Х₂ – выделенная прямая плоскости π´. Отметим на прямой L´K´ точки С´, D´ такие, что трапеция ABCD подобна трапеции A´B´C´D´. Проведём прямые C´F´, D´G´, параллельные прямой B´L´ (F´, G´ лежат на А´В´), и отметим на прямой А´В´ точку Y₁´ такую, что 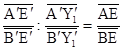, 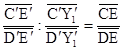. На прямой C´D´ отметим точку Y₂´ такую, что Y₁´Y₂´||A´K´ (см. рис.). Из выбора точек Y₁´ и Y₂´ следует, что прямая Y₁´Y₂´ – выделенная прямая плоскости π´. При преобразовании f точка Е переходит в точку Е´ пересечения прямых A´B´ и L´K´. Точка С переходит в некоторую точку С₀´ прямой С´D´.

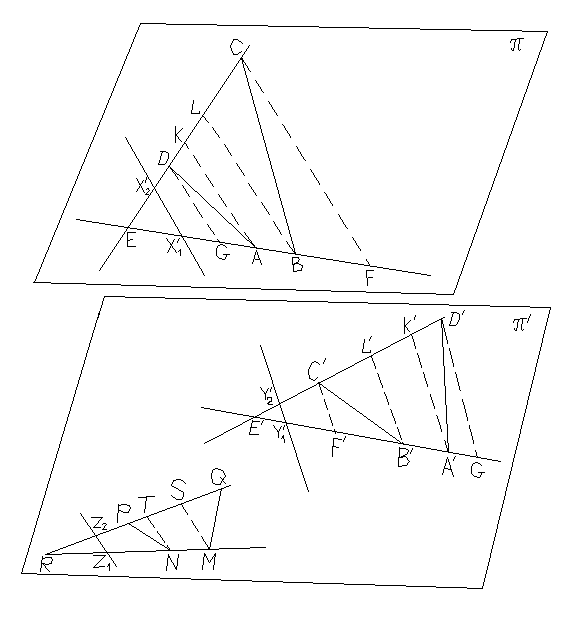
Докажем, что С₀ совпадает с С´. Из того, что Х₂ при преобразовании f переходит в бесконечно удалённую точку прямой C´D´, а Y₂´ - образ бесконечно удалённой точки прямой CD и центральная проекция сохраняет двойные отношения, следует, что 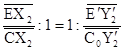, откуда 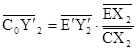. Теперь рассмотрим преобразование g, композицию центральной проекции и подобия, переводящее трапецию CDGF в трапецию C´D´G´F´. Для преобразования g аналогично можно показать, что 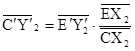. Отсюда будет следовать, что точки С₀ и С´ совпадают. Аналогично можно показать, что D₀ – образ точки D при преобразовании f – совпадает с D´. Итак, преобразование f переводит четырёхугольник ABCD в четырёхугольник A´B´C´D´, подобный четырёхугольнику MNPQ, что и требовалось.

 

Теорема 1.3. Пусть даны четвёрки точек, из которых никакие три не лежат на одной прямой: A, B, C, D и A´, B´, C´, D´. Тогда существует единственное проективное преобразование, переводящее А в А´, В в В´, С в С´, D в D´.

 

Существование такого преобразования следует из теоремы 1.1.

Единственность можно доказывать так же, как и единственность аффинного преобразования (теорема 1.1, часть III): рассматривать квадратную решётку, строить её образ, а затем измельчать. Обойти те трудности, с которыми мы столкнулись при доказательстве аффинной теоремы, нам опять не удастся.

 

Из теорем 1.1, 1.2, 1.3 сразу следуют некоторые важные утверждения:

Следствия.

1. Любое проективное преобразование является композицией центральной (параллельной) проекции и подобия.

2. Проективное преобразование сохраняет двойные отношения.

 

Задача 1.

Даны две прямые a и b и не лежащая на них точка Р. Через Р проводятся различные пары прямых, пересекающих прямые a и b в точках А, С и B, D соответственно. М – точка пересечения AD и ВС. Доказать, что все такие точки М лежат на одной прямой, проходящей через точку пересечения прямых a и b.

Решение.

Пусть О – точка пересечения прямых a и b. Переведём прямую ОР в бесконечно удалённую. Тогда четырёхугольник ABDC будет параллелограммом; М, точка пересечения его диагоналей, будет лежать на прямой, параллельной прямым a и b и отстоящей от них на равные расстояния.

Задача 2.

Можно ли окрасить 2006 точек плоскости в красный цвет и 1003 – в синий так, чтобы любая прямая, проходящая через две точки разных цветов, содержала ещё одну из окрашенных точек и все окрашенные точки не лежали на одной прямой.

Решение.

Рассмотрим проективную плоскость и правильный 2006-угольник на ней. Все вершины 2006-угольника покрасим в красный цвет, а точки пересечения сторон с бесконечно удалённой прямой покрасим в синий цвет. Легко проверить, что этот набор точек обладает требуемым свойством. Осталось лишь сделать проективное преобразование так, чтобы на бесконечно удалённой прямой не осталось отмеченных точек…

Ответ: можно.

Теорема 1.4. Дана окружность и точка M внутри неё. Существует центральная проекция, при которой данная окружность переходит в окружность, а точка M – в её центр.

 

Доказательство. Пусть АВ – тот диаметр нашей окружности, на котором лежит точка M. Рассмотрим косой круговой конус, основанием которого является наша окружность, а вершиной такая точка О, что 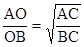. На прямых ОА и ОВ за точку О отложим точки В´ и А´ соответственно так, что ОВ=ОВ´ и ОА=ОА´:

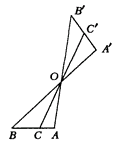
Пусть С´ – середина А´В´ и 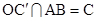. Применяя теорему синусов к треугольникам ОАС, ОВС, ОВ´С´ и ОС´А´, нетрудно получить соотношение 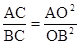, т.е. точка С в точности совпадает с точкой М. Теперь осталось заметить, что из соображений симметрии сечение нашего конуса плоскостью α, проходящей через прямую А´В´ перпендикулярно плоскости (АОВ), является окружностью, поэтому центральная проекция с центром О на плоскость α является искомой.  

Из доказательства этой теоремы следует также

Теорема 1.5: Любое проективное преобразование сохраняет какую-то окружность.

 

Теорема 1.6. Дана окружность и не пересекающая её прямая ℓ. Существует проективное преобразование, переводящее данную окружность в окружность, а ℓ – в бесконечно удалённую прямую.

 

Доказательство. Пусть А, В – произвольные точки прямой ℓ, АK, AL, BM, BN – касательные к окружности из точек А и В, 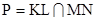. По теореме 1.4 существует преобразование, сохраняющее нашу окружность, переводящее Р в её центр. При этом преобразовании отрезки KL и MN перейдут в диаметры окружности, поэтому А и В перейдут в бесконечно удалённые точки, а ℓ - в бесконечно удалённую прямую.

Задача 3.

Доказать, что прямые, соединяющие вершины треугольника с точками касания противоположных сторон и вписанной окружности, пересекаются в одной точке.

Решение.

Пусть АВС – наш треугольник, А´, В´, С´ – точки касания вписанной окружности со сторонами треугольника, 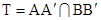. Проведём проективное преобразование, сохраняющее вписанную окружность и переводящее точку Т в её центр. Тогда AA´ и ВВ´ станут одновременно и высотами, и биссектрисами треугольника АВС, т.е. треугольник АВС перейдёт в правильный, а точка Т – в его центр. Значит СС´ проходит через Т.

Проективные теоремы.

Ниже приводятся известные теоремы геометрии, которые легко доказываются применением проективного преобразования:

Теорема 2.1. (теорема Дезарга) Если прямые, содержащие соответственные стороны треугольников ABC и A´B´C´ (т.е. AB и A´B´, BC и B´C´, AC и A´C´), пересекаются в точках P, Q, R лежащих на одной прямой ℓ, то прямые, соединяющие соответственные вершины этих треугольников, пересекаются в одной точке.

 

Теорема 2.2. (теорема Паппа) Если точки А, В, С лежат на прямой ℓ, точки А´, В´, С´ - на прямой ℓ´, то точки P, Q, R пересечения прямых АВ´ и А´В, АС´ и А´С, ВС´ и В´С соответственно лежат на одной прямой.

 

Теорема 2.3. (теорема Паскаля) Точки пересечения противоположных сторон вписанного шестиугольника лежат на одной прямой.

 

Теорема 2.4. (теорема Брианшона) Главные диагонали описанного шестиугольника пересекаются в одной точке.

 

Не будем подробно проводить доказательство этих теорем, покажем лишь, какое преобразование сводит каждую из этих задач к очевидной:

Теорема 2.1 – проективное преобразование, переводящее прямую ℓ в бесконечно удалённую;

Теорема 2.2 – проективное преобразование, переводящее прямую PQ в бесконечно удалённую;

Теорема 2.3 – проективное преобразование, сохраняющее описанную окружность, переводящее прямую PQ в бесконечно удалённую, где P, Q – точки пересечения двух пар противоположных сторон шестиугольника;

Теорема 2.4 – проективное преобразование, сохраняющее вписанную окружность, переводящее точку пересечения двух диагоналей в центр этой окружности.