Инверсия пространства.

Определение.Пусть в пространстве дана сфера S с центром О и радиусом R. Инверсией относительно сферы S называется преобразование, переводящее произвольную точку А, отличную от О, в точку А´, лежащую на луче ОА такую, что 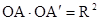. S – сфера инверсии, О – центр, R – радиус инверсии.

Дополним пространство бесконечно удалённой точкой и поставим её в соответствие точке О (тогда, очевидно, бесконечно удалённая точка перейдёт при инверсии в точку О).

Будем считать, что любая прямая и любая плоскость содержат бесконечно удалённую точку пространства.

Определение. Углом между двумя пересекающимися сферами называется угол между касательными плоскостями к сферам, проведёнными через любую из точек пересечения сфер. Углом между пересекающимися сферой и плоскостью называется угол между касательной плоскости к сфере, проведённой через любую из точек пересечения сферы и плоскости, и данной плоскостью.

Определение. Углом между двумя пересекающимися окружностями (окружностью и прямой) в пространстве называется угол между касательными к окружностям, проведёнными через любую из точек пересечения окружностей. Углом между пересекающимися окружностью и прямой называется угол между касательной к окружности, проведённой через любую из точек пересечения окружности и прямой, и данной прямой.

С помощью движений пространства легко доказать корректность этих определений (т.е., что угол не зависит от точки пересечения сфер (окружностей), которую мы рассмотрели). Например, для сфер можно перевести одну точку пересечения в другую, сохранив сферы, поворотом вокруг оси, проходящей через центры сфер.

Свойства инверсии.

1. Преобразование, обратное инверсии, – та же инверсия.

2. Прямая (плоскость), проходящая через точку О, переходит в себя.

3. Прямая (плоскость), не содержащая точку О, переходит в окружность (сферу), проходящую через точку О.

4.  Окружность (сфера), содержащая точку О, переходит в прямую (плоскость), не содержащую О.

5. Сфера, не содержащая точки О, переходит в сферу.

6. Окружность, не содержащая точки О, переходит в окружность.

7. Сохраняется угол между пересекающимися сферами (плоскостями, сферой и плоскостью).

8. Сохраняется угол между пересекающимися окружностями (прямыми, окружностью и прямой).

9. Если А´, В´ - образы точек А, В, то .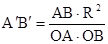

10. Если сфера S´ - образ сферы S, то О – центр гомотетии, переводящей S в S´.

Доказательства свойств.

Свойства 1-5, 7, 9, 10 доказываются аналогично свойствам инверсии на плоскости.

Свойство 6 следует из того, что окружность можно представить в виде пересечения двух сфер.

Докажем свойство 8. Будем говорить, что окружности (окружность и прямая) касаются, если они лежат на одной сфере (в одной плоскости) и имеют ровно одну общую точку. Как легко видеть, касающиеся окружности (окружность и прямая) переходят при инверсии в касающиеся окружности (окружность и прямую) или параллельные прямые. Поэтому угол между образами окружностей равен углу между образами касательных прямых, проведённых через точку касания.

Итак, утверждение достаточно доказать для пересекающихся прямых. При инверсии с центром О эти прямые переходят в окружности, проходящие через О. Причём касательные к ним в точке О параллельны этим прямым, т.е. угол между ними сохраняется.

Задача.

Семь вершин выпуклого шестигранника, все грани которого – четырёхугольники, лежат на одной сфере. Доказать, что и восьмая вершина этого шестигранника лежит на этой сфере.

Решение.

Пусть ABCDA₁B₁C₁D₁ – наш шестигранник, и пусть для определённости вершина D₁ – та вершина, про которую не известно, лежит ли она на данной сфере. Сделаем инверсию с центром в точке В. При этой инверсии данная сфера перейдёт в некоторую плоскость α. Точки B₁´, C₁´, C´, D´, A´, A₁´, образы точек B₁, C₁, C, D, A, A₁, лежат в плоскости α, причём точки C₁´, D´, A₁´ лежат на сторонах треугольника B₁´C´A´ (см. рис.).

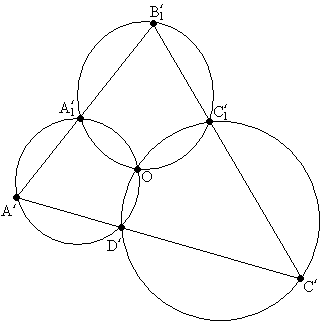
Плоскости (B₁A₁C₁), (CDC₁), (DAA₁) перейдут в сферы, описанные около тетраэдров BB₁´A₁´C₁´, BC´D´C₁´, BD´A´A₁´. Точка D₁ перейдёт в точку пересечения этих сфер, отличную от В. Фактически нам надо показать, что эта точка лежит в плоскости α. Для этого достаточно показать, что окружности, описанные около треугольников B₁´A₁´C₁´, C´D´C₁´, D´A´A₁´, пересекаются в одной точке. А это уже простой факт планиметрии. Действительно, пусть окружности, описанные около треугольников B₁´A₁´C₁´, C´D´C₁´, пересекаются в точке О. Тогда, как легко убедиться, 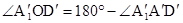, и окружность, описанная около треугольника D´A´A₁´, проходит через точку О. Доказательство завершено.