Классификация движений пространства.

Пользуясь доказанными теоремами, можно классифицировать все движения пространства.

Мы хотим доказать общую теорему:

Теорема 7.0. Любое движение пространства есть параллельный перенос, винтовое движение, поворот вокруг оси, зеркальная симметрия, поворотная симметрия или переносная симметрия.

Для этого удобно разбить все движения по классам. И для каждого класса определить все движения, входящие в этот класс. Для начала разобьём все движения на движения I и II рода и докажем две теоремы, из которых сразу следует теорема 7.0:

Теорема 7.1. Любое движение I рода есть параллельный перенос, винтовое движение или поворот вокруг оси.

Теорема 7.2. Любое движение II рода – это зеркальная симметрия, поворотная симметрия или переносная симметрия.

Для доказательства этих теорем удобно разбить движения на классы по количеству неподвижных точек. Теперь мы получим четыре теоремы, каждая из которых в отдельности доказывается несложно:

Теорема 7.1.а. Любое движение I рода, имеющее хотя бы одну неподвижную точку, является поворотом вокруг оси.

Теорема 7.1.б. Любое движение I рода, не имеющее неподвижных точек, есть параллельный перенос или винтовое движение.

Теорема 7.2.а. Любое движение II рода, имеющее хотя бы одну неподвижную точку, является зеркальной симметрией или поворотной симметрией.

Теорема 7.2.б. Любое движение II рода, не имеющее неподвижных точек, есть переносная симметрия.

Эти теоремы фактически доказывают теоремы 7.1 и 7.2.

Будем доказывать их не по порядку, т.к. при доказательстве некоторых теорем удобно использовать другие.

Пусть f – данное движение.

Доказательство теоремы 7.1.а. Утверждение – простое следствие теоремы 6.5 (теоремы Даламбера), согласно которой f можно представить композицией двух зеркальных симметрий. Если плоскости симметрии параллельны, то f – параллельный перенос, что невозможно, т.к. у параллельного переноса нет неподвижных точек. Значит, плоскости симметрии пересекаются по некоторой прямой ℓ. Тогда, как легко показать, f – поворот вокруг оси ℓ на удвоенный ориентированный угол между плоскостями симметрии.

Доказательство теоремы 7.2.а. Возможны два случая: f – зеркальная симметрия или f – композиция трёх зеркальных симметрий (теорема 6.4). В первом случае и доказывать нечего. Во втором случае рассмотрим неподвижную точку О нашего преобразования f . Теперь рассмотрим движение . У движения g точка О неподвижная. С другой стороны, g – движение I рода (т.к.  меняет ориентацию). Отсюда (теорема 7.1.а) g – поворот вокруг оси, содержащей точку О. Но 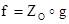, т.е. f – поворотная симметрия.

Доказательство теоремы 7.2.б. Пусть А´ – образ некоторой точки А при движении f, α – плоскость симметрии точек А и А´. Тогда движение  первого рода имеет неподвижную точку А´. По теореме 7.1.а движение g – поворот вокруг оси. Пусть . Тогда , откуда , причём ℓ||α, иначе общая точка ℓ и α будет неподвижной точкой движения f. Как мы уже говорили, композицией двух зеркальных симметрий (если плоскости симметрий не параллельны) будет поворот вокруг общей прямой плоскостей симметрий на удвоенный ориентированный угол между плоскостями симметрий. Отсюда понятно, что поворот вокруг оси можно представить композицией двух зеркальных симметрий. Плоскости симметрий должны обе содержать ось поворота, причём одну из этих плоскостей в остальном можно выбрать произвольно. Представим , выбрав плоскость β перпендикулярной плоскости α. Тогда . Заметим, что  – осевая симметрия S_u, где . Причём u||γ, т.к. u параллельна прямой ℓ, лежащей в плоскости γ. S_u можно представить композицией двух зеркальных симметрий , где . При этом получится π||γ. Тогда , причём  – вектор, перпендикулярный плоскостям γ и π, т.е. ||σ. Таким образом,  – переносная симметрия.

Доказательство теоремы 7.1.б. Опять возьмём произвольную точку А, её образ А´ при движении f и плоскость ω симметрии точек А и А´. Тогда движение  второго рода имеет неподвижную точку А. По теореме 7.2.а движение g – зеркальная симметрия или поворотная симметрия.

Если g – зеркальная симметрия, то f является композицией двух зеркальных симметрий. Кроме того f не имеет неподвижных точек, т.е. f – параллельный перенос.

Пусть теперь  ( ) – поворотная симметрия. Представим  ( ), причём выберем . Тогда . Т.к. , ,  и  – осевые симметрии. Итак,  – композиция двух осевых симметрий.

Если a и b пересекаются, то у f есть неподвижная точка, что невозможно.

Если a и b параллельны, то f, как легко убедиться, – параллельный перенос.

Если а и b скрещиваются, то рассмотрим их общий перпендикуляр h и прямую p такую, что p проходит через точку пересечения h и a и p||b. Тогда, как легко убедиться,  – поворот вокруг прямой h на некоторый угол, а  – параллельный перенос на некоторый вектор . Поэтому  – винтовое движение. 

Пользуясь, полученными результатами получаем таблицу:

Часть II. Подобия пространства.

Определение. Подобием 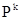 называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение , где k – некоторое фиксированное положительное число (называемое коэффициентом подобия).

Определение. Фигура Ф называется подобной фигуре Ф´, если существует подобие, переводящее Ф в Ф´.