Метод двухсторонней оценки

При проектировании реальных сетей обычно отсутствует необходимость точного расчета надежности сети, так как исходные данные по надежности элементов задаются, как правило, с некоторой конечной точностью. Проектировщикам необходимо лишь убедиться в том, что надежность сети, с одной стороны, не ниже заданной и, с другой стороны, не имеет экономически необоснованного запаса. Другими словами, на практике достаточно гарантировать, что истинное значение надежности 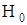 находится в некоторых пределах Hmin<  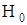< Hmax.

Можно ожидать, что оценка надежности сети с заданной конечной точностью позволит сократить трудоемкость расчетов в тем большей мере, чем ниже требуемая точность оценки. Действительно, при расчете надежности по совокупности путей, добавление каждого следующего пути приводит к увеличению надежности, а при расчете по совокупности сечений добавление каждого следующего сечения приводит к уменьшению структурной надежности, что создает предпосылки для двусторонней оценки структурной надежности с гарантированной точностью по ограниченным наборам путей и сечений. Рассмотрим эту возможность более подробно.

Обозначим через 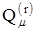 результат, полученный при перемножении вероятностей отказов  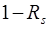первых r из общего числа n путей. Тогда с учетом следующего (r + 1) пути согласно (1.13) получим уточненную оценку  :

 

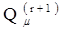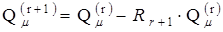                   (1.17)

 

Функция 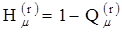 является монотонно неубывающей с возрастанием r и при  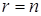дает точное значение 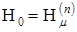. Промежуточные значения  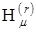при 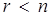 можно рассматривать, как оценки  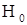снизу. Аналогично, исходя из формулы (1.15), можно получить монотонно не возрастающую последовательность 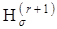, которую можно рассматривать, как последовательность оценок  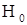сверху. Характер зависимост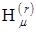и  и 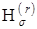 от r представлен на рисунке 1.5. Опыт показывает, что рассматриваемые зависимости при малых r меняются весьма круто, а с дальнейшим увеличением r очень медленно приближаются к общему пределу 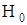. Это свойство можно использовать для сокращения трудоемкости оценок надежности с заданной точностью. Действительно, для решения задачи достаточно последовательно просматривать пути μ, пока не выполнится условие 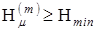, а затем просматривать сечения σ, пока не выполнится условие 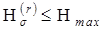. Если для некоторого m окажется, что 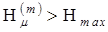, то можно прекратить расчеты и принять решение, что в сети заложена излишняя избыточность. Если же для некоторого r окажется, что 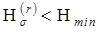, то это значит, что требования к надежности сети не выполняются. Число требующих просмотра путей m и сечений r обычно гораздо меньше общего числа путей n и общего числа сечений k (m << n, k << r), чем и достигается сокращение трудоемкости оценки. Одновременно гарантируется, что истинное значение надежности сети лежит в заданных пределах, а именно: .

 

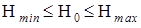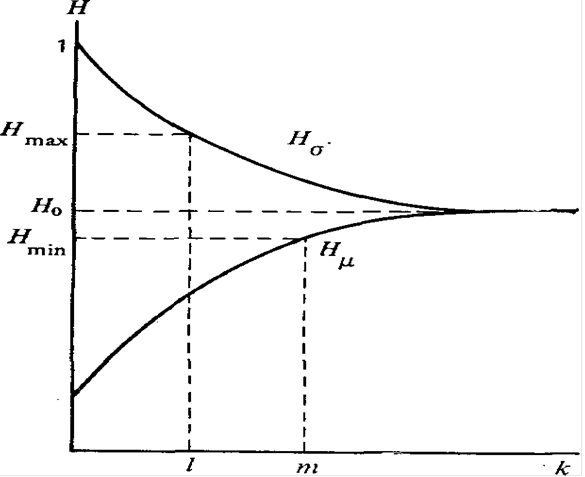
Рисунок 1.5. Характер изменения оценок структурной надежности по совокупности путей и сечений

 

Точность оценки может быть задана в виде допустимых отклонений от ис­тинного значения 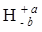. В этом случае просмотр путей и сечений следует вести до тех пор, пока не выполнится условие 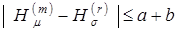. В частности, если 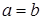, то условие прекращения расчетов имеет вид 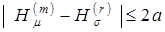,а в ка­честве оценки надежности следует принять следующую величину:

 

.

 

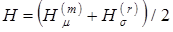В ходе расчетов, решения о рассмотрении на следующем шаге очередного пути или сечения целесообразно принимать по критерию большего абсолютного приращения надежности по соответствующему параметру, то есть по m или r.

Пример. Пусть необходимо оценить надежность сети, представленной графом на рисунке 1.6, с точностью H ± 0,01. Узлы сети идеально надежны. Линии, обозначенные буквами, имеют одинаковую надежность .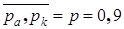

Выпишем первые несколько путей и сечений, которые могут потребоваться для расчета:

 

М' = { аbс, def, abhf, dgbc...};

S' = { ad, be, cf, age...}.

 

Полные множества путей М и сечений S для рассматриваемого метода можно не выписывать. При необходимости, если на начальном подмножестве М', S' не удается достичь необходимой точности, эти подмножества можно будет расширить по ходу расчетов.

Поскольку первые два пути из М' независимы, можно сразу записать начальную нижнюю оценку вероятности несвязности сети:

 

.

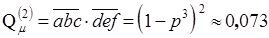Переходя к оценке надежности, 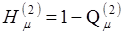, получаем 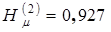. Начальную верхнюю оценку надежности можно получить по первым трем независимым сечениям множества S':

 

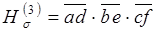. (1.18)

 

При рассмотрении сечений запись вида 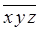 интерпретируется как наличие, по крайней мере, одного исправного элемента в сечении, поэтому при подстановке исходных данных в (1.18) получим:

 

.

 

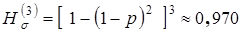Разница между полученными верхней и нижней оценками составляет 0.044, что больше 0.02, поэтому необходимо продолжить расчет.

Добавление следующего пути дает большее абсолютное приращение надежности, чем добавление следующего сечения. Поэтому вводим в рассмотрение очередной путь abhf из множества М' согласно формуле (1.17):

 

.

 

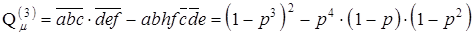
Отсюда получаем очередную оценку надежности снизу

 

.

 

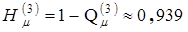Убеждаемся, что заданная точность еще не достигнута и добавление очередного пути снова даст большее абсолютное приращение надежности, поэтому вводим следующий путь dgbc из множества М' для уточнения нижней границы надежности:

 

,

 

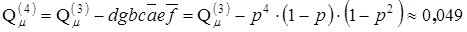что соответствует .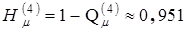

Разница между верхней и нижней оценками надежности теперь составляет: 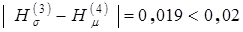, что позволяет прекратить расчеты, так как заданная точность H ± 0,01 достигнута. В качестве оценки надежности рассматриваемой сети принимаем среднеарифметическое  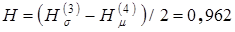с гарантией, что 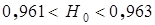. При этом из полного множества, включающего девять сечений и восемь путей, нам удалось ограничиться рассмотрением всего трех сечений и четырех путей.

 

 

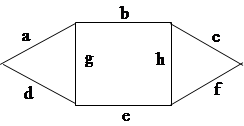Рисунок 1.6. - Пример сети для двусторонней оценки надежности

 

Для разветвленных сетей связи использование предлагаемого метода позволяет значительно сократить трудоемкость расчетов, по сравнению с методом полного перебора путей или сечений, а также гарантирует любой заданный уровень точности, в оценке вероятности события – сеть связанна.

 

1.2.4 Метод статистической оценки структурной надежности

Широко распространенным методом оценки надежности сложных технических систем является метод статистических испытаний. Однако для получения статистически достоверных результатов, особенно при высокой исходной надежности элементов системы и ее большой структурной избыточности, требуются значительные затраты машинного времени.

Опыт показывает, что основные затраты времени при статистических испытаниях сложной системы сопряжены с проверкой ее работоспособности в каждой реализации [6]. При высокой исходной надежности pi элементов или большой структурной, избыточности, характерной для разветвленных сетей коммутации, проверка на работоспособность подавляющего большинства реализации дает положительный результат, что обусловливает их малую информативность. Поэтому возникает естественное желание найти некоторое преобразование сети, позволяющее искусственно уменьшить исходную надежность ее элементов, чтобы быстрее набрать необходимую статистику отказов и получить обратное преобразование, позволяющее пересчитывать получаемые результаты на реальные показатели надежности элементов сети. Покажем, что такая возможность действительно существует.

Назовем разрезом подмножество элементов системы, удаление которых приводит к потере работоспособности. Рассмотрим некоторый разрез u, в который входит ровно z элементов. Частота выпадения такого разреза при статистических испытаниях стремится по ходу испытаний к ее вероятности :

 .

 

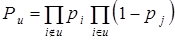Если обозначить через N общее число элементов сети, то вероятность Ри можно записать в виде:

.

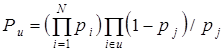Изменим исходные показатели надежности системы таким образом, чтобы каждый сомножитель 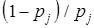 второго произведения увеличился в γ раз. Другими словами, вместо элемента с надежностью pj введем элемент с надежностью p'j такой, чтобы удовлетворялось условие:

 

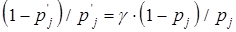(1.19);

 

Тогда надежность нового элемента будет определяться формулой:

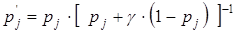.(1.20)

 

Если произвести преобразование (1.19) для всех элементов сети, то вероятность выпадения разреза u в процессе испытаний изменится и составит:

 

;

 

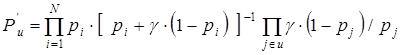Введем коэффициент 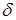 увеличения частоты выпадания разреза

 

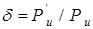(1.21)

 

тогда, подставляя в (1.21) старое и новое значения частоты выпадания разреза u, получим:

 

.

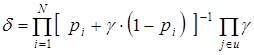Если в разрез u входит ровно z элементов, то:

 

,

 

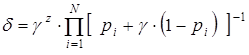где второй сомножитель является константой для исходной системы. Отсюда следует, что предлагаемое преобразование показателей надежности не приводит к нарушению относительной частоты появления разрезов фиксированного веса z, так как коэффициент убыстрения для всех этих разрезов одинаков. Однако, относительная частота появления разрезов веса z + w, по сравнению с разрезами веса z, увеличивается в 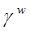 раз. Поэтому в ходе статистических испытаний преобразованной системы можно набрать достаточную статистику по разрезам большего веса, вероятность появления которых в исходной системе бывает обычно очень малой.

Пересчет вероятности появления разреза u из преобразованной системы в исходную производится в соответствии с (1.21):

 

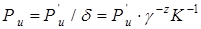(1.22)

 

Для выполнения обратного преобразования (1.22) кроме факта отказа системы необходимо фиксировать и вес z соответствующего разреза.

Из (1.22) следует, что каждый случай появления разреза u с весом z в преобразованной системе соответствует 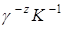 случаям появления такого же разреза в исходной системе. При этом если; в преобразованной системе за время испытаний произошло m отказов, то для исходной системы эквивалентное число отказов будет выражаться следующим выражением:

 

,

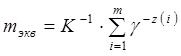где 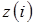 – число элементов, вышедших из строя при i-м отказе системы.

При возникновении очередного отказа m в преобразованной системе оценки надежности Рm исходной системы уточняются в соответствии с выражением:

 

,

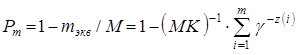где 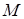 – общее число просмотренных реализации состояний преобразованной системы.

Возникает вопрос, каким следует выбирать параметр преобразования γ для максимального убыстрения процесса статистических испытаний конкретной системы? Из (1.20) следует, что при γ = 1 изменение исходной надежности не происходит и убыстрение отсутствует. Если выбрать γ слишком большим, то в преобразованной системе будут в основном возникать разрезы большого веса, не характерные для исходной системы, причем их вклад в результирующую надежность при больших z в соответствии с (1.22) будет невелик. Поэтому параметр γ следует выбирать таким образом, чтобы максимизировать вероятность возникновения наиболее “ вероятных ” разрезов.

Рассмотрим этот вопрос более подробно. Для простоты положим, что показатели надежности всех элементов системы одинаковы и равны р. Обозначим через P(z) вероятность возникновения отказовых состояний веса z. Очевидно, что вероятность потери работоспособности системы тогда будет:

 

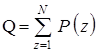.(1.23)

Обычно для реальных систем значение 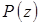 достаточно плавно меняется с увеличением веса разреза, поэтому в качестве наиболее вероятного разреза можно выбрать класс разрезов среднего веса.

 

.

 

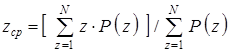Для надежных систем в выражении (1.23) можно пренебречь всеми членами, кроме первого ненулевого, соответствующего минимальному разрезу веса 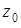, который и будет наиболее вероятным. Таким образом, задача состоит в том, чтобы максимизировать коэффициент убыстрения для наиболее вероятного разреза, т. е. найти максимум функци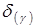и  при , ,  :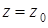

 

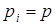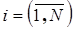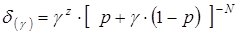.(1.24)

 

Из условия 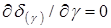 получаем оптимальное значение

 

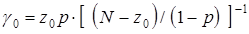.(1.25)

 

Подставляя выражение (1.25) в (1.20), нетрудно убедиться, что оптимальное значение 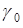 соответствует пересчитанному значению надежности элемента системы 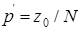. Другими словами, для максимального убыстрения процедуры статистических испытаний необходимо таким образом пересчитать надежность элементов системы, чтобы средний вес отказов в преобразованной системе соответствовал весу наиболее вероятного разреза.

Убыстрение темпа набора статистики отказов в соответствии с (1.24), когда 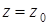, составит:

 

.

 

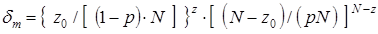Так, для системы с параметрами p = 0,99, N = 20, z0 = 3 время испытаний можно сократить приблизительно в 150 раз для достоверности получаемых результатов не хуже, чем в случае прямого набора статистики отказов системы.

 

2 ИССЛЕДОВАНИЕ СТРУКТУРНОЙ НАДЕЖНОСТИ МЕТОДОМ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

 

2.1 Критерии оценки структурной надежности методом статистического моделирования

 

Современные сети коммутации имеют весьма сложную структуру [7]. Прежде всего, необходимо сформулировать критерий отказа сети.

Через сеть обменивается информацией большое число пар абонентов, причем часто требуется, чтобы вероятность наличия связи между корреспондентами выделенной пары (r, l) была не менее заданной Рrl. Под наличием связи понимается существование, по крайней мере, одного исправного пути между соответствующими узлами. Конечно, в сложной сети наличие исправного пути еще не гарантирует немедленного установления соединения, так как элементы этого пути могут быть заняты для обмена информацией других корреспондентов. Однако, если предположить, что термин “наличие связи” относится только к информации высшей категории (доля которой в реальных сетях обычно весьма мала) и элементы любого исправного пути способны обеспечить обмен этой информацией в интересах всех корреспондентов, которые им могут воспользоваться, то возникает возможность рассматривать все пары корреспондентов независимо с точки зрения наличия связи между ними. В элементах сети, производительность которых недостаточна для обслуживания суммарной нагрузки высшей категории, можно предусмотреть большее число s рабочих компонентов.

Таким образом, сеть обладает заданной надежностью, если вероятность наличия связи или, как говорят, вероятность связности Hrl для каждой пары узлов не менее заданной Рrl. В этих условиях расчет структурной надежности сети сводится к расчету вероятности связности между узлами.

Следующим критерием оценки структурной надежности является интегральный критерий. По этому критерию сеть считается исправной (связной), если имеется связь между всеми ее узлами и задается требование на вероятность такого события.

Последний критерий как раз и используется при оценке структурной надежности сети методом статистического моделирования.

 

2.2 Разработка алгоритма расчета структурной надежности

 

2.2.1 Алгоритм расчета структурной надежности сети

связи методом статистического моделирования

Опишем сначала принцип расчета структурной надежности сети методом статистического моделирования [4].

Сеть связи задают в виде вероятностной матрицы смежности 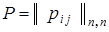, где 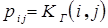 – элемент матрицы, отражающий величину надежности линии связи между узлом 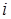и узлом 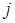, а 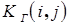 – коэффициент готовности данной линии связи 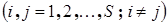. В свою очередь коэффициент готовности может быть определен по следующей формуле:

 

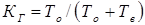(2.1)

 

где 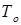 – время наработки на отказ,  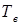– среднее время восстановления.

Производится  независимых испытаний, каждое из которых можно условно разделить на два этапа.

На первом этапе вырабатывают 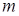 независимых случайных, равномерно распределенных в интервале  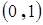чисел 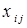. Затем, значения  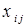последовательно сравниваются с величинами  по следующему алгоритму:

если 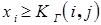 – элемент сети отказал, результат равен нулю;

если 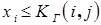 – элемент сети находится в исправном состоянии, результат равен единице.

Результаты сравнения записываются в матрицу , .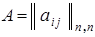

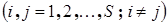На втором этапе производится проверка структуры сети, которая описана матрицей 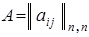, на связность. Если сеть связна, то исход испытания относится к числу благоприятных .

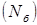Результатом оценки структурной надежности сети является значение 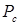 – отношение числа благоприятных исходов к общему числу испытаний.

Проверка сети на связность может осуществляться, например, на основе процедуры “соединения”. Ее суть заключается в следующем.

На анализируемой сети выбирается произвольный узел. Далее находят смежные ему узлы и соединяют с ним. Это происходит до тех пор, пока сеть не представится в виде одного узла – “точки” (в случае если, сеть связана) или множества узлов (если сеть не связана).

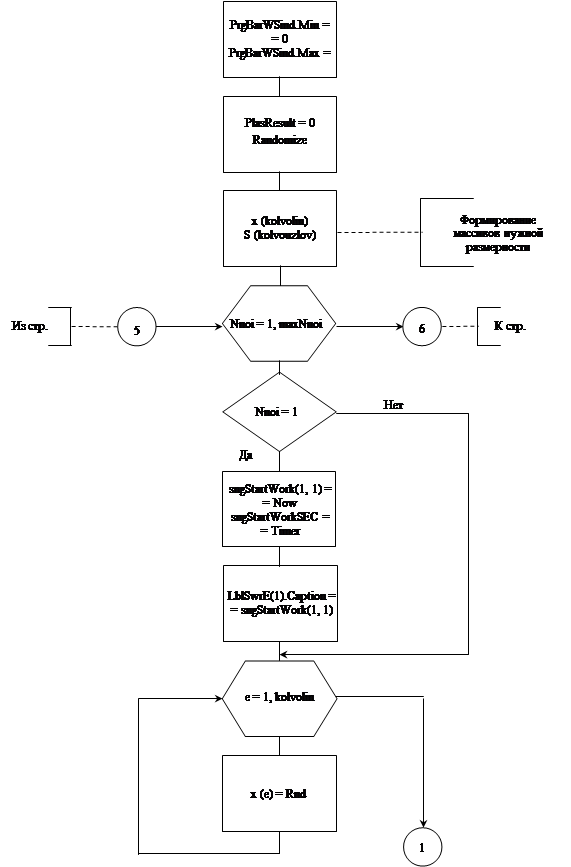
Разработанный на основе всего выше изложенного алгоритм программы, в общем виде, отобразим на рисунке 2.1. Опишем с начала переменные, используемые в этом алгоритме:

i, e и j – переменные используемые в циклах типа for – next основной процедуры расчета надежности сети;

PlasResult – хранит число благоприятных исходов;

x( ) – динамический массив, равномерно распределенных в интервале (0, 1) чисел;

Nnoi – хранит текущий номер испытания;

maxNnoi – хранит общее число испытаний;

PP – хранит значение вероятности события – сеть связна;

Imeny – хранит номер случайно выбранного узла;

S( ) – динамический массив, для хранения номеров смежных узлов;

Nnew – хранит информацию о наличии новых смежных вершин;

sngStartWork(1, 2) – массив дат начала и конца расчета надежности сети;

sngStartWorkSEC – хранит число секунд расчета надежности сети;

bar – промежуточная переменная для хранения текущего номера испытаний.

 

 

 

 

 

 

 

 

 

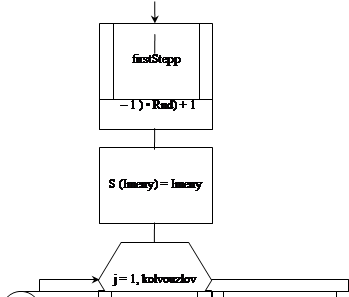Рисунок 2.1 – Алгоритм расчета структурной надежности сети

Отобразим более подробно алгоритмы тех процедур, которые непосредственно участвуют в определении события – сеть связна. Алгоритмы этих процедур разместим в порядке их вызова основной программой расчета структурной надежности сети связи методом статистического моделирования. Порядок вызова этих процедур и краткое описание их задачи сведем в таблицу 2.1.

 

Таблица 2 .1 – Процедуры определения связности сети

Имя процедуры	Задача процедуры
VektStrok Nnew, Imeny, S, A	Соединение смежных узлов
SvjazNet Imeny, A, p	Проверка на единичность полученной вектор-строки
FinishAnswer A, PlasResult, Imeny, p, S, Nnew	Вынесение решения о связности сети, проверка наличия новых смеж­ных узлов для формирования нового массива смежных узлов

 

 

Рисунок 2.2 – Алгоритм процедуры “ VektStrok ”

 

 

Рисунок 2.3 – Алгоритм процедуры “ SvjazNet ”

 

 

 

 

Рисунок 2.4 – Алгоритм процедуры “ FinishAns wer ”

2.2.2 Алгоритм интерфейсной части программы расчета надежности сети методом статистического моделирования

 

Приведем рисунок алгоритма программы интерфейса.

 

 

 

 

 

	Нет		Да