Статистические методы регулирования качества технологических процессов при контроле по количественному признаку

Количественные данные представляют собой наблюдения, полученные с помощью измерения и записи значений некоторой характеристики для каждой единицы, рассматриваемой в подгруппе, например длина в метрах, сопротивление в омах, шум в децибелах и т.д. Карты для количественных данных, и особенно простейшие из них ( 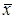–и 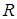–карты), – это классические контрольные карты, применяемые для управления процессами.

Контрольные карты для количественных данных имеют следующие преимущества:

а) большинство процессов и их продукция на выходе имеют характеристики, которые могут быть измерены, так что применимость таких карт потенциально широка);

б) измеренное значение содержит больше информации, чем простое утверждение «да – нет»;

в) характеристики процесса могут быть проанализированы безотносительно установленных требований. Карты запускаются вместе с процессом и дают независимую картину того, на что процесс способен. После этого характеристики процесса можно сравнивать или нет с установленными требованиями;

г) хотя получение количественных данных дороже, чем альтернативных, объемы подгрупп для количественных данных почти всегда гораздо меньше и при этом намного эффективнее. Это позволяет в некоторых случаях снизить общую стоимость контроля и уменьшить временной разрыв между производством продукции и корректирующим воздействием [3].

При контроле по количественному признаку используют следующие виды контрольных карт:

1) средних арифметических значений ( 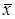–карта);

2) медиан ( 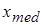– карта);

3) средних квадратических отклонений ( 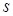– карта);

4) размахов ( 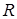– карта) [4].

Контрольная карта средних арифметических значений 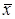 имеет наибольшее распространение на практике и используется для статистического регулирования уровня настройки оборудования.

В дальнейшем предполагается, что контролируемый признак 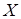 имеет нормальный закон распределения с математическим ожиданием  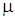и средним квадратическим отклонением 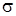. Периодически для контроля отбирается постоянное число изделий 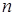, по которым определяется средняя арифметическая:

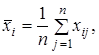 (2.1)

где 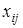 – результат контроля 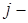го изделия 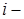й выборки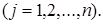

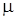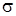Ввиду того, что параметры  и  генеральной совокупности  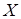неизвестны, на практике их оценивают по результатам предварительного анализа не менее 100 изделий, изготовленных на данном оборудовании. Например, если для ведения контрольной карты используют выборку объемом  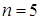изделий, то при оценивании можно воспользоваться результатами последних  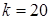выборок с общим числом  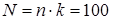проконтролированных изделий.

Пусть по каждой выборке рассчитаны средни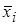е , где 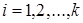. Тогда общая средняя арифметическая  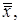которая принимается в качестве оценки математического ожидания 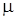, равна:

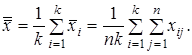 (2.2)

Для оценки дисперсии 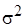генеральной совокупности  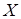по результатам предварительного анализа вычисляют выборочную дисперсию

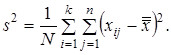 (2.3)

В качестве оценки среднего квадратического отклонения генеральной совокупности 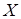 используют .

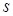Вычисление 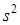 является громоздким. Поэтому на практике часто оценку параметра  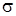получают с помощью вариационного размаха 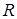. Пусть по результатам 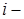й выборки  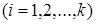вычислен размах :

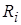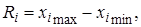 (2.4)

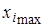где  и 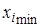– соответственно максимальное и минимальное значения признака в 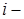й выборке.

Отсюда

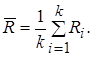 (2.5)

Отметим, что 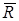 учитывает рассеяние только внутри выборок. Доказано, что 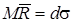, где 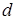– коэффициент, зависящий от объемы выборки 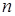. Точность оценивания  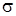с помощью размаха  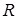резко падает с возрастанием 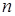, поэтому размах  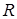используют при  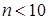изделий.

Задача определения контрольных границ на контрольной карте средних арифметических значений сводится к нахождению границ критической области при проверке на уровне значимости 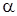 нулевой гипотезы 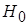:  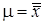против конкурирующей гипотезы 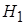: 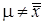. В основу критерия для проверки гипотезы положена выборочная характеристика

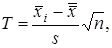 (2.6)

которая при 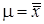 имеет нормированное нормальное распределение с нулевым математическим ожиданием  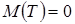и с единичной дисперсией 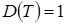. Тогда нижняя и верхняя границы критической области равны:

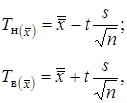 (2.7)

где 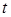 определяется по таблице интегральной функции  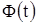(табл. П.1 [6]).

Часто на практике принимают 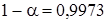, тогда 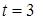. В выражении 2.3 за значение параметра  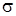принимают соответствующие оценк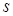и  или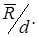

На контрольную карту средних арифметических значений наносят среднюю линию с ординатой 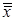 и контрольные границы  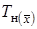и .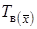

Определение средней арифметической 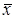 по выборке объема  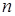связано с определенной вычислительной работой, которую часто трудно выполнить в условиях производства. В этих случаях более предпочтительной оценкой математического ожидания  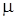является медиана 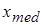. Хотя она менее эффективна, чем средняя 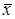, но ее проще определить. Например, если требуется определить медиану по данным  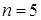наблюдений, то мы должны расположить наблюдения в порядке их возрастания  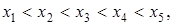тогда медиана будет равна значению среднего признака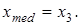

Верхние и нижние границы контрольной карты медиан определяют как

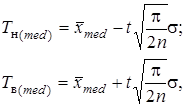 (2.8.)

Где

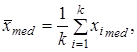 (2.9)

где 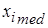 – значение медианы, найденное по результатам 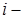й выборки.

Методы оценки параметра 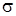 генеральной совокупности рассмотрены выше.

Для статистического регулирования показателей точности оборудования используют контрольные карты средних квадратических отклонений (s–карта) и размахов (R–карта). Среднюю линию и контрольные границы этих карт также определяют по результатам предшествующего анализа.

Среднюю линию на s–карте определяют из условия

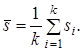 (2.10)

Расчет контрольных границ s–карты сводится к определению границ критической области критерия проверки гипотезы 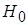:  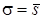против конкурирующей гипотезы 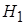:  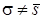на уровне значимости 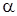. Критерий проверки гипотезы основан на выборочной характеристике

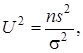 (2.11)

которая имеет распределение 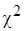 с 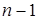 степенью свободы.

Примем 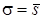 и по таблице распределения  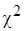(табл. П.3 [6]) для числа степеней свободы  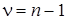определим граничные значения  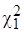и 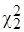 из условия:

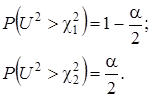 (2.12)

Нижняя и верхние контрольные границы на контрольной карте равны:

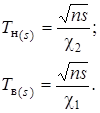 (2.13)

При построении контрольной карты размахов средняя линия 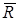 определяется по уравнению 2.5., а контрольные границы из условия:

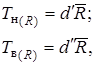 (2.14)

где значения коэффициентов 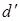 и 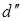 протабулированы в [9], [10] для объема выборки  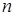от 2 до 10.

В практике статистического регулирования технологических процессов получили распространение «двойные карты». Применение таких карт основано на том, что для характеристики процесса важно знать не только среднее значение контролируемого признака, но и рассеяние признака около среднего значения, т.е. показатели точности процесса. Например, двойная контрольная карта средних арифметических значений и размахов содержит две рабочие зоны – для средней арифметической 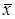 и размаха  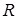с контрольными границами [6].