Собственные колебания и формы

Собственными называются периодические колебания консервативной системы, совершающиеся исключительно под воздействием инерционных и упругих сил. Консервативные системы не содержат диссипативных звеньев, рассеивающих энергию.

Для возбуждения таких колебаний достаточно приложить к системе какое-нибудь начальное возмущение, т.е. вывести ее из состояния равновесия. После прекращения действия возмущения в системе устанавливаются собственные колебания с частотами 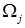. Углы поворота масс равны

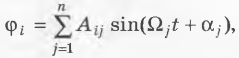
где i – номер массы;

j – порядковый номер собственной частоты;

 – фазовый угол;

А_ij – амплитуда колебаний i-й массы на j-й собственной частоте.

Из формулы следует, что в общем случае все массы системы совершают сложное колебательное движение, называемое полигармоническим. Можно выбрать такие начальные возмущения, при которых все массы будут совершать гармонические колебания с некоторой одной частотой , но с разными амплитудами:

Эти колебания называют главными или нормальными колебаниями.

Одинаковый фазовый угол  означает, что массы системы одновременно проходят через положение равновесия и одновременно достигают максимальных значений. Совокупность амплитуд называют формой колебаний. У каждой собственной частоты имеется своя форма колебаний, называемая главной. Число форм колебаний равно числу собственных частот системы. В теории колебаний доказывается, что энергия одной формы колебаний не может переходить в энергию колебаний другой формы.

Рисунок – Формы колебаний и упругие линии неразветвленной пятимассовой динамической модели:

–––––––– – для первой формы; - - - - - - – для второй формы

Матричный метод определения собственных частот динамической модели

В общем виде для рассчитываемой консервативной модели составляются уравнения движения, которые затем записываются в преобразованиях Лапласа. Полученную систему алгебраических уравнений записывают в систематизированном виде и составляют характеристический определитель. Затем его преобразовывают в частотный определитель R(w) заменой оператора s на jw (или s² на –w²). Таким образом, получают частотное уравнение в виде определителя. Например, для модели с четырьмя парциальными системами:

где R_i = λ_i-w_i. i = 1,4 – частотные уравнения парциальных систем;

λ_i – квадраты собственных частот парциальных систем;

r_i,i+1 – коэффициенты связи одной парциальной системы с другой.

Описанный выше метод нахождения частотного уравнения известен в литературе как матричный метод.