Прохождение детерминированного сигнала через линейные звенья.

Для описания процесса прохождения сигнала через линейные звенья с постоянными параметрами применяют :

- спектральный метод;

- метод суперпозиции.

Спектральный метод (метод спектрального разложения) основан на использовании передаточной функции или частотной характеристики K(j w).

Если входной сигнал

, то выходной сигнал

, где

.

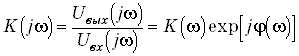K(w) определяет как бы вес отдельных спектральных составляющих входного сигнала в их вкладе в выходной сигнал, j(w) -фазовый сдвиг выходного сигнала относительно входного.

Метод суперпозиции (метод интеграла наложения) состоит в том, что сложный входной сигнал представляют в виде совокупности очень коротких импульсов и рассматривают выходной сигнал системы как сумму реакций на эти сигналы. Выходной сигнал системы при воздействии единичного импульса, т. е. дельта-функции, называется импульсной характеристикой системы и обозначается g(x). Так как спектр единичного импульса равен единице для всех частот, то

,

т.е. частотная и импульсная характеристики системы являются парой преобразования Фурье.

Отсюда ясно, что функцию K(j w) можно определить экспериментально, исследуя реакцию системы на единичный импульс. Например, на вход системы подается короткий импульс, сигнал с выхода поступает на анализатор спектра, в результате находится частотная характеристика K(j w).

В оптике короткому импульсу аналогична мира в виде точки. Распределение энергии в кружке рассеяния, т.е. в изображении точки, определяет импульсную характеристику (весовую функцию) оптической системы.

Найдем в общем виде выражение для выходного сигнала и_вых(х), если на вход линейного звена или системы поступает сигнал и_вх(х) , а импульсная характеристика системы g(x) известна. Для этого сигнал произвольного вида можно разбить на элементарные импульсы и найти реакцию системы на любой из этих импульсов с координатой x₁ для произвольного значения аргумента х (рис. 2.3).

Рис.2.3. К выводу (2.9)

Если площадь какого-либо элементарного импульса равна единице, то его можно рассматривать как дельта-функцию, возникающую при значении аргумента x₁. В этом случае импульсная реакция для произвольного значения х_i равна g(x_i -x₁). Поскольку площадь одиночного импульса на входе равна u_вх(х₁ ) Dх₁, а не единице, то выходная реакция на такой сигнал будет u_вх(х₁ ) Dх₁g(x_i -x₁).

Складывая результаты действия отдельных элементарных импульсов в точке х_i нужно перейти к интегрированию последнего выражения, т.е. к интегралу свертки

.(2.9)

Для системы, у которой g(x) =g*(-x) и g(x_i-x₁) =g*(x₁-x_i), (2.9) можно переписать в виде

,

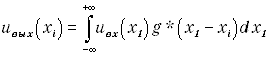т.е. выходной сигнал является функцией взаимной корреляции входного сигнала и функции, комплексно-сопряженной с импульсной реакцией. Это часто применимо к оптическим системам.

 2.2. Случайные сигналы и способы их описания

Случайным сигналом принято называть величину, которая может принимать любые значения в определенном интервале с определенной вероятностью.

Основными характеристиками случайных величин являются:

§ § ·интегральный закон (функция) распределения случайной величины х;

§ § ·плотность распределения или дифференциальный закон распределения р(х);

§ § ·математическое ожидание М(х);

§ § · дисперсия D=s² или среднее квадратическое значение (стандарт) s.

Одним из наиболее распространенных на практике является гауссовский (нормальный) дифференциальный закон распределения

.

Математическим ожиданием или средним значением дискретного случайного сигнала х является сумма произведений всех возможных значений х_i на соответствующие им вероятности р_i, т.е. для конечного числа п значений х_i

 или , так как .

Для непрерывной случайной величины х математическое ожидание, являющееся начальным моментом первого порядка,

.

Математическое ожидание центрированной случайной величины х—М(х) равно нулю.

ДисперсиейD дискретной случайной величины является математическое ожидание квадрата отклонения значения случайной величины от ее математического ожидания, т. е. центральный момент второго порядка

Для непрерывной случайной величины

.

Семейство случайных скалярных или векторных величин, зависящих от скалярного параметра (например, времени, пространственной координаты и др.), с заданными конечномерными функциями распределения случайных величин называется случайной функцией или случайным процессом. В практике ОЭП часто встречаются случайные функции не одного, а нескольких аргументов, например двух координат на плоскости и времени. При фиксированном значении аргумента одномерная случайная функция превращается в обычную случайную величину.

В отличие от характеристик случайных величин, представляемых определенными числами, характеристики случайных функций являются в общем случае не числами, а функциями. Так, математическое ожидание случайной функции s(x) является неслучайной функцией аргумента х, равной при каждом значении этого аргумента математическому ожиданию сечения случайной функции, т. е.

Дисперсией случайного процесса s(x) называется неслучайная функция D_s(x), значение которой для каждого х равно дисперсии случайной величины х, т.е. дисперсии соответствующего сечения случайной функции:

Случайные сигналы считаются стационарными, если их характеристики (математическое ожидание, дисперсия, другие начальные или центральные моменты) не зависят от аргумента (от начала отсчета аргумента) случайной функции.

Стационарный случайный процесс очень часто обладает эргодическим свойством — усреднение его характеристик по множеству реализаций случайного процесса с вероятностью, близкой к единице, эквивалентно усреднению по одной его реализации при достаточно большом изменении аргумента.

Ковариационной функциейстационарного случайного процесса s(x) называется математическое ожидание произведения значений этого процесса s₁ и s₂, взятых для аргументов х и х+Dх, или второй смешанный начальный момент, т. е. выражение вида

где * - знак сопряженности функции.

Для центрированного случайного процесса пользуются понятием «корреляционная функция», которая определяется как второй смешанный центральный момент

где М_s(х) и М_s(х+ Dх) - математические ожидания сечений случайного процесса s(x) для аргументов х и х+Dх.

Ковариационная и корреляционная функции связаны между собой следующим соотношением: