Детерминированные сигналы и способы их описания

Сигналом принято называть физический процесс, несущий информацию — совокупность сведений, являющихся объектом передачи, преобразования, хранения или непосредственного использования. В ОЭП основным носителем информации является электромагнитное излучение.

Сигналы могут быть:

- - ·детерминированными и случайными;

- - ·непрерывными и дискретными;

- - ·периодическими и непериодическими.

Детерминированные сигналы, т.е. такие, у которых в любой момент времени или в любой точке пространства (внутри исследуемой области) все значения известны, подразделяются на:

- - периодические;

- - непериодические.

Каждый из них может быть :

§ § - непрерывным;

§ § - дискретным.

Случайные оптические сигналы характеризуются пространственной и временной неоднородностью излучения и описываются случайными функциями. Как правило, случайными сигналами являются шумы и помехи, возникающие в различных звеньях ОЭП и вне его.

Характерным примером детерминированного сигнала является идеальный единичный импульс, описываемый дельта-функцией, свойства которой определяются следующими соотношениями:

Последнее выражение является интегралом свертки функций d (x) и f(x) и определяет так называемое фильтрующее свойство дельта-функции. Пользуясь им, можно показать:

1. 1. интеграл свертки (или просто свертка) функций f(x-x₁) и дельта-функции d(х-х₂) равен f(x-x₁-x₂),

2. 2.  свертка двух дельта-функций d(х-х₁) и d(х-х₂) дает d(х-x₁-х₂) .

Периодический сигнал s(x) любой формыможно представить в виде суммы простых гармонических составляющих (гармоник) разложением s(x) в ряд Фурье, если функция s(x) удовлетворяет условию Дирихле (является кусочно-ограниченной и имеет конечное число экстремумов на протяжении периода X):

 

где  — среднее значение функции s(x);  коэффициенты ряда Фурье; y_n=arctg(b_n/a_n ) — фаза n-й гармоники; Х — период; w₁=2p/X — частота первой гармоники; п — целые числа.

 — гармоники в комплексном представлении ряда Фурье, имеющие одинаковые амплитуды и разные по знаку фазы.

При сложении С_n и С_-n дают действительную функцию аргумента х, т.е. амплитуду реального «физического» колебания, поскольку ехр(jwx)+exp(-j wx)=2cos (wx).

Для четных функций s(x) = s(-x) коэффициент b_n=0;

для нечетных s(x) = -s(-x) коэффициент a_n=0.

Совокупность отдельных гармоник образует спектр функции, который для периодического сигнала дискретен. Отдельные составляющие дискретного спектра отстоят друг от друга на величину w₁=2p/Х. Можно отметить, что при увеличении скважности импульсов (отношение периода следования импульсов к их длительности) линии спектра сближаются, а сам он приближается к сплошному.

Для непериодического сигнала (Х®Ґ) ряд Фурье вырождается в интеграл Фурье, т.е. спектр становится сплошным. В этом случае

 (2.1)

 (2.2)

Выражения (2. 2) и (2. 1) называют соответственно прямым и обратным преобразованием Фурье. Они применимы к абсолютно интегрируемым функциям, для которых сходится интеграл вида .

Для функций s(x), четных относительно х, интегралы в (2.1) и (2.2) совершенно подобны и переменные w и х взаимозаменяемы. В этом легко убедиться, если учесть, что

Огибающая S (j w ) (модуль спектра или спектральной плотности) совпадает по форме с огибающей дискретного спектра периодической функции, полученной из непериодической её повторением с периодом Y , и отличается только масштабным множителем w ₁ /p. Таким образом, если известен вид спектра одиночного сигнала, например, одиночного импульса, то спектр последовательности таких импульсов можно легко найти. Рассмотрим несколько примеров

Модуль спектра прямоугольного импульса протяженностью Х_И с амплитудой Е (рис. 2.1, а)

 

Рис.2.1. Сигналы и их спектры:а — одиночный прямоугольный импульс; б — дельта-функция; в — периодическая последовательность прямоугольных импульсов

При wX_И/2<<1, т.е. при приближении к дельта-функции, имеем

Таким образом, модуль спектра дельта-функции (рис. 2.1,б)

.(2.3)

Последнее выражение можно также получить, используя фильтрующее свойство дельта-функции. Пользуясь преобразованием Фурье, а также учитывая четность дельта-функции, можно представить её условное определение в виде

.(2.4)

Последовательность импульсов прямоугольной формы (рис.2.1,в) описывается рядом

 при

где Y_И -период импульсной последовательности. Спектр этой последовательности состоит из отдельных гармоник, отстоящих друг от друга на w₁=2p/Y_И, и имеет модуль.

Огибающая амплитуд гармоник повторяет огибающую спектра одиночного прямоугольного импульса.

Напомним некоторые свойства преобразования Фурье (теоремы о спектрах), необходимые для дальнейшего изложения.

1. 1. Свойство взаимности. Если повторно применить прямое преобразование Фурье к спектру S(jw) функции s(x), то можно восстановить центрально-симметричный исходный сигнал, т. е.

Действительно, если S(jw) — спектр функции s(x), то с учетом (2.1) можно записать

2. 2. Свойство симметрии. Преобразования Фурье обладают свойством симметрии.

Действительно, если вычислить преобразование для функции s*(x), комплексно-сопряженной с s(x), то получим

Для действительной функции s(x) = s*(x)

Для действительной четной функции s(x) = s*(x) = s*(-x)

3. 3. Свойство линейности (теорема о спектре суммы). Если S₁(jw) и S₂(jw) — спектры функций s₁(x) и s₂(x) соответственно, а a и b — произвольные комплексные числа, то спектр суммы as₁(x)+ bs₂(x), являющейся линейной комбинацией s₁(x) и s₂(x), равен линейной комбинации соответствующих спектров, т. е.

4. 4. Теорема подобия. Если S(jw) - спектр функции s(x), то для любой действительной постоянной а спектр функции s(ax) равен S(jw/a)/a. Если заменить ах на у, то

Таким образом, в результате сжатия сигнала по координате х, ведущего к изменению функции в а раз быстрее, увеличиваются частоты, составляющие её спектр, и изменяются амплитуды гармоник.

5. 5. Теорема запаздывания.

Спектр S₀(jw) функции s(x-x₀) отличается от спектра S(jw) функции s(x) множителем ехр (-jwx₀). Действительно, если сдвинуть функцию s(x) на х₀, то её спектр будет

Заменяя переменную интегрирования х на y=x-x₀, получим

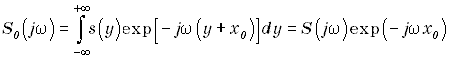
Заметим, что модуль спектра остается неизменным, т.е.

Применительно к случаю дельта-функции d(x-x₀)

6. 6. Теорема о переносе спектра. Если сместить спектр S(jw), которому соответствует функция s(x), по шкале частот на величину W (действительное число), то сдвинутому спектру S [j(w+W)] соответствует функция

.

Действительно,

т. е. соответствующая этому спектру функция

7. 7. Теорема о спектре свертки. Спектр S (jw) свертки

двух функций s₁(x) и s₂(x) равен произведению спектров S₁(jw) и S₂(jw) исходных функций s₁(x) и s₂(x).

Действительно,

8. 8. Теорема о спектре произведения (обратная теорема свертки). Произведению функций s₁(x) и s₂(x) соответствует спектр S₁₂(w), являющийся сверткой спектров S₁(jw) и S₂(jw) исходных функций. Из свойства взаимности преобразований Фурье

и теоремы о спектре свертки следует, что для свертки спектров S₁(jw) и S₂(jw)

преобразование Фурье S₁₂(jw)=2ps₁ (x₁)s₂(x₂). Отсюда спектр произведения исходных функций

Важным для практики следствием из теорем о спектрах является равенство Парсеваля, определяющее, что полная энергия процесса, описываемого функцией s(y), равна полной энергии спектра:

,

что можно доказать, если рассмотреть свертку s(x) для x=0. При этом свертка

Отсюда, учитывая свойство симметрии преобразований Фурье, т.е. тот факт, что при замене s₂(у) на s₂*(-у) происходит замена S₂(jw) на S₂*(jw), а также предполагая s₁(y) = s₂(y) = s(y), легко получить равенство Парсеваля.

Определим вид спектра сложной периодической функции, являющейся суммой отдельных гармоник, используя интегральное преобразование Фурье.

Если , то, применяя преобразование Фурье к обеим частям этого равенства, получим

С учетом (2.4)

,

.(2.6)

Одной из основных особенностей оптических приборов и ОЭП является то, что сигнал часто нельзя представить одномерной функцией. Информацию об излучающем объекте можно описать функцией двух переменных (например, в виде функции координат в плоскости изображения) или более (например, как функцию трех линейных координат, длины волны, времени).

Так, двумерную дельта-функцию можно использовать как модель точечного излучателя, находящегося в начале координат:

 при

или в векторной форме

 при

В этих случаях преобразования Фурье можно записать в многомерной форме, например в двумерной:

или в векторной форме

где w_х, w_у - так называемые пространственные частоты по осям х и y соответственно (см. ниже);  — вектор пространственной частоты; ( ) — «формальное» скалярное произведение векторов  и ;  — область плоскости вектора с бесконечно большими пределами.

Пространственная частота является мерой повторяемости оптического сигнала, например яркости объекта или освещенности изображения, вдоль какого-либо направления, например, вдоль ортогональных осей х и у. Величины w_x и w_y связаны с числами пространственных периодов Х и Y на единицу длины, т.е. с циклическими пространственными частотами f_x и f_y: w_x=2pf_x =2p/X; w_y=2p/Y.

Часто пространственную частоту рассматривают как меру повторяемости по углу, т.е. размерность w_x, w_y, w_r или соответственно f_x, f_y, f_r может быть обратно пропорциональной размерности не только линейной величины, но и угловой.

В тех случаях, когда в качестве независимых переменных используются не прямоугольные координаты х и у, а полярные - r и a , причем х=r cos a, y=r sin a, для нахождения пространственно-частотного спектра S(j w _r ) удобно использовать не преобразование Фурье, а преобразование Ганкеля:

где J_n( ) - функция Бесселя первого рода n-го порядка.

Обратное преобразование имеет вид

Если s(r, a) симметрична относительно центра полярной системы координат, т. е. ее форма определяется только радиусом r, то

Для дальнейшего рассмотрения удобно определить вид спектра функции s(x, y) в том случае, когда один из ее аргументов, например, у, фиксируется, оставаясь постоянным, т. е. служит параметром. В этом случае с точностью до постоянной можно записать

где d(w_y ) - дельта-функция аргумента w_y .

Приведем некоторые используемые на практике преобразования Фурье:

- прямоугольной двумерной функции

 при

- двумерной центрально-симметричной функции Гаусса

;

;

- круга равной яркости L₀:

 при

,

где J₁ — функция Бесселя первого рода 1-го порядка.

Помимо разложения в ряд Фурье нам в дальнейшем понадобится и другое разложение, известное как теорема Котельникова. Оно представляет собой разложение функции у(х), имеющей ограниченный спектр (от 0 до f_max), по ортогональным функциям y(х), причем коэффициенты этого разложения y_k являются дискретными значениями у(х), взятыми через интервал Dх, т.е.

,(2.7)

где çkú=0, 1, 2, 3, ...; y_k(x)=y(kDx); Dx=1/(2f_max);

.

Функции y_k(x) обладают свойством ортогональности, т. е.

 при  (2.8)

Из (2. 7) и (2. 8) можно получить выражение для энергии сигнала

.

Для конечного интервала значений х (0... х) действительны разложения вида (2.7) c заменой пределов интегрирования в (2.8) на 0... х и суммирования на 1... n, где п=х/∆х=2f _maxx.

При п>> 1 погрешность от перехода к новым пределам невелика, т.е. в интервале 0...х функция у(х) полностью определяется п выборками из нее.

Рассмотрим две функции (рис. 2.2). Очевидно, что для дискретизации функции у₁(х) (рис. 2.2,а) требуется большее число составляющих, т. е. Dх у нее меньше, чем у функции y₂(x) (рис. 2.2,б). Также очевидно, что первую функцию можно представить рядом или интегралом Фурье с большим числом составляющих. Это согласуется с данным выше определением: чем больше f_max, тем меньше должен быть интервал Dх.

Рис.2.2. Представление непрерывных функций дискретными значениями