Внутренняя геометрия поверхности

Содержание

Глава 1.Введение в дифференциальную геометрию поверхностей. Основные понятия

1.1 Первая квадратичная форма поверхности

1.2 Внутренняя геометрия поверхности

1.3 Вторая квадратичная форма поверхности

1.4 Классификация точек регулярной поверхности

1.5 Средняя и гауссова кривизны поверхности

Глава 2. Понятие поверхности Каталана

2.1 Общие положения

2.2 Примеры поверхностей Каталана

2.3 Виды поверхностей Каталана

Глава 3. Дифференциальная геометрия поверхностей Каталана

3.1 Первая и вторая квадратичные формы линейчатой поверхности

3.2 Первая и вторая квадратичные формы поверхности Каталана

3.3 О коноидах

Глава 4. Специальные поверхности Каталана (поверхности класса КА)

4.1 Вывод уравнения поверхности класса КА

4.2 Вывод уравнения поверхности класса КА по заданным кривым и нормальному вектору порождающей плоскости

Глава 5. Дифференциальная геометрия поверхностей класса КА

5.1 Первая и вторая квадратичные формы линейчатой поверхности

5.2 Первая квадратичная форма поверхности класса КА

5.3 Вторая квадратичная форма поверхности класса КА

Глава 6. О программе визуализации и анализа поверхностей

6.1 Общие положения и возможности программы

6.2 Примеры работы

Выводы

Список литературы

Глава 1. Введение в дифференциальную геометрию поверхностей.

Основные понятия

Первая квадратичная форма поверхности

 

Пусть  - гладкая поверхность,  – ее векторное параметрическое уравнение и .

Определение 1.1.

Первой квадратичной формой на поверхности  называется выражение

 

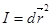                                                                                                     (1)

 

Распишем это выражение подробнее.

 

,

Откуда                                                               (2)

 

Выражение (2) в каждой точке поверхности  представляет собой квадратичную форму от дифференциалов  и 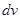. Первая квадратичная форма является знакоположительной, так как ее дискриминант

 

 и .

 

Для коэффициентов первой квадратичной формы часто используют следующие обозначения (и мы в своих исследованиях будем придерживаться именно их) ([1].[2],[3]):

,

,

.

 

Так что выражение (2) для формы  можно переписать в виде

 

                                                                           (3)

 

Соответственно,

 

.

 

Внутренняя геометрия поверхности

 

Известно, что, зная первую квадратичную форму поверхности, можно вычислять длины дуг кривых на поверхности, углы между кривыми и площади областей на поверхности. В самом деле, если рассмотреть формулы, определяющие вышеуказанные величины, можно заметить, что туда входят только лишь коэффициенты 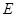, ,  первой квадратичной формы. Поэтому если известная первая квадратичная форма поверхности, можно исследовать геометрию на поверхности, не обращаясь к ее уравнениям, а лишь используя ее первую квадратичную форму.

Совокупность геометрических фактов, относящихся к поверхности, которые можно получить при помощи ее первой квадратичной формы, составляет так называемую внутреннюю геометрию поверхности.

Поверхности, имеющие одинаковые первые квадратичные формы и потому имеющие одинаковую внутреннюю геометрию, называются изометричными.

Рассмотрим простой пример.

Пусть задана поверхность

 

 

Это цилиндрическая поверхность с синусоидой в качестве направляющей.

 

 

Имеем:

 

,

 

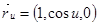Поэтому

 

,

,

 

Следовательно,

 

.

 

Если сделать замену, вводя новые параметры  и  таким образом

,

.

 

Тогда первая квадратичная форма поверхности примет, очевидно, вид

 

.

 

Мы видим, что в новых переменных первая квадратичная форма рассматриваемой цилиндрической поверхности совпадает с первой квадратичной формой плоскости  и поэтому внутренняя геометрия этой поверхности совпадает с внутренней геометрией плоскости. Т.е. синусоидальный цилиндр изометричен плоскости. Этот важный факт мы еще получим несколько другим способом.

Чисто геометрически это свойство понятно: синусоидальный цилиндр получается изгибанием (т.е. деформацией без сжатий и растяжений) обычной плоскости. При такой деформации внутренняя геометрия не изменяется.

Более того, можно показать, что если одна поверхность получается из другой путем изгибания, то внутренние геометрии этих поверхностей совпадают.