Глава 2. Понятие поверхности Каталана

Общие положения

Определение 2.1.

Поверхность Каталана – линейчатая поверхность, прямолинейные образующие которой параллельны одной и той же плоскости.

Определение 2.2.

Плоскость, которой параллельны образующие поверхности Каталана, называется плоскостью параллелизма.

Определение 2.3.

Поверхность Каталана, все образующие которой пересекают одну прямую, называется Коноидом.

Замечание 2.1.

Обычно предполагают, что уравнение поверхность Каталана:

 

, причем .

 

Мы, однако, не будем учитывать это условие, а ограничимся указанным выше определением. И те, и другие поверхности мы будем для краткости называть поверхностями Каталана.

Замечание 2.2.

Из определения поверхности Каталана следует, что, если ее уравнение:

 

, то .

 

Это очевидно, так как все три вектора (вычисленные при одном и том же значении параметра), участвующие в смешанном произведении лежат в одной плоскости, – плоскости параллелизма, т.е. они компланарны.

Для обратного утверждения справедлива теорема.

Теорема 2.1.

Достаточное условие того, что данная линейчатая поверхность является поверхностью Каталана.

Пусть задана линейчатая поверхность

 

,

 

причем вектор-функция 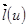 трижды непрерывно дифференцируема (здесь и далее мы говорим о каком-либо простом куске поверхности, которому отвечают некоторые промежутки параметров). Тогда если и  неколлинеарен  ни в одной точке то данная поверхность является поверхностью Каталана.

Доказательство.

Рассмотрим два случая: когда кривая, описываемая вектором  – плоская и когда она неплоская.

1) Предположим, что кривая 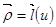 – плоская. Тогда равенство  просто следует из этого факта. Очевидно, что все тройки векторов (при любом значении параметра) лежат в плоскости кривой . Поэтому и все образующие лежат в этой плоскости, значит и поверхность является по определению поверхностью Каталана.

2) Предположим, что кривая 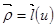 – неплоская. По условию теоремы . Продифференцируем это равенство один раз по параметру:

 

.

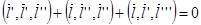
Если  коллинеарен вектору 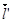 в некоторой точке. Тогда

 

 

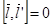
Значит  коллинеарен , а значит,  коллинеарен и , а мы предположили противное, значит, этот случай невозможен, т.е.  неколлинеарен вектору .

Посмотрим на картинку:

 

 

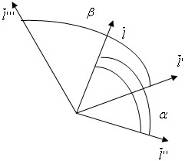
Так как , то все эти три вектора лежат в одной плоскости – плоскости . А в силу того, что , эти векторы тоже лежат в одной плоскости – плоскости  (в первом случае плоскость обозначена двумя дугами, во втором, одной дугой). Так как векторы  и  неколлинеарны, то они в обоих случаях определяют плоскость, т.е. плоскости  и  – совпадают, а значит, все четыре вектора: , , ,  лежат в одной плоскости, а значит: .

Напомним, что если дана кривая . То кручение кривой в точке  вычисляется по формуле:

                                                                       (*)

 

Т.к.  – то кривая  – плоская, а это противоречит предположению пункта два. Т.е. рассматриваемая ситуация невозможна.

Таким образом, кривая 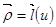 (в условиях теоремы) может быть только плоской кривой и при этом поверхность является поверхностью Каталана ч.т.д.

Замечание 2.3. Если в теореме убрать предположение о тройной непрерывной дифференцируемости вектор-функции . То можно построить пример поверхности, такой что , но при этом поверхность не является поверхностью Каталана.

Красивый пример можно получить следующим образом.

Нам хочется, чтобы функция  «развернула» плоскость прямых или разворачивала ее постоянно. Как следует из теоремы, соответствующую функцию следует искать среди функций, 3-яя производная которых терпит в какой-либо точке разрыв.

Например, можно задаться следующим уравнением: .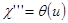

Здесь  – функция Хэвисайда.

Проинтегрируем это уравнение.

 

.

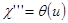
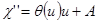
Теперь уже гораздо проще подобрать необходимый пример.

Итак, рассмотрим поверхность.

 

 

Проверим, что в каждой точке выполняется равенство: .

 

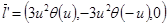
Замечание 4. Строго говоря, мы тут допустили неточность. А именно: . Т.е. производная тета-функции Хэвисайда – дельта-функция Дирака. Поэтому,

 

.

 

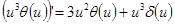Однако, простое геометрическое рассуждение может убедить нас, что вторым слагаем можно пренебречь. Действительно, посмотрим на график функции:

 

 

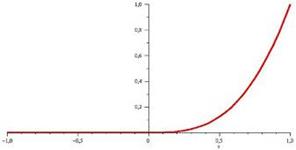
Очевидно, что в нуле наклон касательной к графику функции равен нулю, а функция  равна нулю всюду, кроме, быть может, нуля, следовательно, вклад в значение производной эта функция не вносит. Таким образом, Наше выражение для производной вполне корректно.

 

.

 

Проверим условие коллинеарности векторов  и .

 

 

Как мы видим, они коллинеарны в каждой точке.

Теперь нам надо отыскать три прямые, которые вместе не лежат в параллельных плоскостях.

Для этого найдем три значения направляющего вектора этих прямых.

,

,

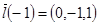Если эти три вектора некомпланарны, то отвечающие им прямые (для которых они являются направляющими векторами) не лежат в параллельных плоскостях, т.е. являются искомыми.

.

Т.е. эти прямые действительно не лежат в параллельных плоскостях.

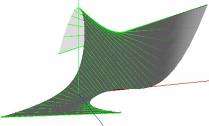
Ниже на рисунке изображен пример такой поверхности. Мы отчетливо видим, как на этой поверхности есть прямы, соответствующие данным векторам.

 

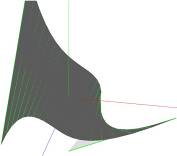
Более простой пример можно построить, убрав требование о том, что  неколлинеарен .

Найдем вектор, который в каждой точке обладает свойством, обратным к данному.

Пусть  коллинеарен вектору 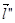 при каждом значении параметра. Например:

 

Пусть .

 

Решим уравнение, например, для координаты .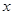

 

 

Сделаем замену: .

 

.

.

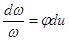Подставим в .

 

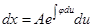
. Т.е. 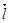 имеет вид:

 

Вычислим производные для проверки.

 

,

.

 

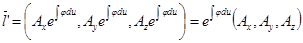Теперь видно, что в каждой точке векторы  и 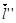 коллинеарные, поэтому смешанное произведение будет заведомо равно нулю (другого и быть не могло, собственно).

Теперь нам надо сделать так, чтобы нашлись 3 вектора 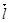 не лежащие в одной плоскости (при соответствующих значениях параметра).

Т.е.

 

,

,

.

И при этом: .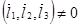

Поскольку сдвиг в пространстве всех этих трех векторов не повлияет на равенство (или не равенство) нулю смешанного произведения, то достаточно рассматривать векторы:

 

,

,

.

 

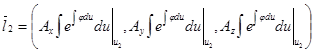А эти векторы, очевидно, лежат в одной плоскости. Так что добиться выполнения утверждения о коллинеарности векторов 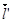 и 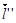 в каждой точке, при выполнении, которого поверхность не будет являться поверхностью Каталана – нельзя.

Значит, стоит подумать о примере, который обеспечивает выполнение этого условия в одной точке, в которой, разумеется, мы должны «повернуть» плоскость образующих линейчатой поверхности.

Рассмотрим вектор:

 

 

Очевидно:

 

,

 

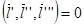Очевидно, что  в каждой точке (есть нулевой столбец). Также, за исключением точки, соответствующей параметру  кручение вектора  также равно нулю ( ). Причем, в каждой точке промежутка:  неколлинеарен  (т.е. мы имеем право пользоваться формулой (*) для расчета кручения кривой на указанном промежутке).

Действительно:

 

Если : , .

 

График ординаты имеет вид:

 

 

И мы видим, что он нигде кроме 1 в нуль не обращается (это видно и непосредственно из аналитического выражения).

Если : , .

 

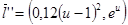Аналогично – график на данном полуинтервале:

 

 

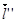Теперь мы уже поняли, что  коллинеарен в точке . Следовательно, вычислять кручение кривой в этой точке по формуле (*) нельзя. Как мы сейчас увидим, в результате – кривая  не будет плоской.

Действительно, возьмем три вектора:

 

,

,

.

 

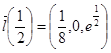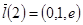Проверим, лежат ли они в одной плоскости.

 

.

 

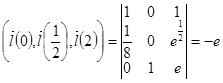Действительно, они некомпланарны, а следовательно, и соответствующие этим векторам прямые не лежат в одной плоскости, значит, поверхность не является поверхностью Каталана.

Теперь осталось написать явно хороший пример такой поверхности.

Пусть

 

 

Примерный вид такой поверхности изображен ниже на рисунке.