Средняя и гауссова кривизны поверхности

 

Нам осталось рассмотреть еще немного понятий, прежде чем приступить к исследованиям. Рассмотрим на поверхности  произвольную  - регулярную кривую, проходящую через точку  в направлении .

Пусть

 

 

- естественная параметризация кривой. Вычислим в точке  три вектора

- единичный вектор касательной к кривой

 

,

 

- единичный вектор нормали к поверхности

- и вектор

 

 

Эта тройка векторов линейно независима. Это позволяет представить вектор

 

 

в виде линейной комбинации

 

Так как 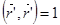, то

 

.

 

Коэффициенты 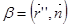 и  имеют специальные названия.

 – нормальная кривизна кривой

 – геодезическая кривизна кривой.

Примем без доказательства следующую формулу для вычисления нормальной кривизны поверхности в заданном направлении

 

                                                                        (1)

 

Как видно из этой формулы нормальная кривизна поверхности в данной точке зависит от направления на поверхности.

Определение 1.3.

Направление на поверхности называется главным, если нормальная кривизна в этом направлении достигает экстремального значения.

Покажем, что в каждой точке -регулярной поверхности найдется не мене двух различных главных направлений.

Пусть  – произвольное направление в точке  на поверхности . Тогда

 

                                                                             (2)

(2) – дифференцируемая функция переменных  и . Отметим, что функции коэффициентов второй и первой квадратичных форм определяются только выбором точки  и от переменных  и  не зависят.

Полагая

 

,

 

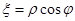получим, что

 

 

Так как функция

 непрерывна и , то на отрезке  она либо постоянна, либо имеет хотя бы один максимум. Это и означает, что в каждой точке  - регулярной поверхности есть два различных главных направления.

Определение 1.4.

Экстремальные значения нормальных кривизн в главных направлениях называются главными кривизнами поверхности в данной точке.

Укажем способ вычисления главных кривизн в данной точке регулярной поверхности.

Из формулы (2) вытекает тождество относительно переменных  и

 

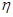
                                                   (3)

 

Продифференцируем это тождество по . Учитывая, что производная нормальной кривизны в главном направлении обращается в нуль, получим для главного направления

 

                                                                         (4)

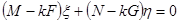                                                                        (5)

 

Здесь 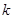 – главная кривизна в направлении .

Рассматривая полученные соотношения (4) и (5) как систему линейных алгебраических уравнений относительно неизвестных 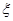 и , получим, что эта система всегда имеет ненулевое решение, так как в данной точке регулярной поверхности всегда есть главные направления.

Из этого вытекает, что

 

 

Вычисляя определитель, мы получим квадратное уравнение для искомой функции 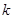 (внимание… мы его будем использовать при некоторых выкладках далее).

 

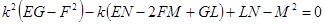                                           (6)

 

Возможны два случая.

Случай 1.

Квадратное уравнение имеет два различных корня  и .

Этим корням на поверхности соответствует два различных главных направления.

Случай 2.

Уравнение (6) имеет один корень кратности 2 .

Это могут быть только точки уплощения  или омбилические точки (точки округления) ( ).

Определение 1.5.

Средней кривизной  поверхности в данной точке называется полусумма ее главных кривизн в этой точке.

 

                                                                                          (7)

 

Определение 1.6.

Гауссовой кривизной 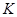 поверхности называется произведение ее главных кривизн.

 

                                                                                                   (8)

 

В виду уравнения (6) можно показать, что

 

                                                                             (9)

                                                                                         (10)

 

Этих основных понятий нам пока хватит для рассмотрения специального класса поверхностей.