 |
Главная |
Первая и вторая квадратичные формы поверхности Каталана
|
из
5.00
|
Итак, из формулы (5), (6), (7):
 . (5)
. (5)
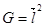 . (6)
. (6)
 . (7)
. (7)
Для поверхности Каталана мы имеем дополнительное условие  . Тут мы не получим никаких существенных изменений.
. Тут мы не получим никаких существенных изменений.
Определитель
 ,
,
индекс 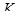 говорит о том, что он вычислен для поверхности Каталана.
говорит о том, что он вычислен для поверхности Каталана.
Расчет  .
.
 (8)
(8)
Расчет M .
 .
.
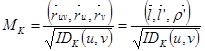 . (9)
. (9)
Расчет N .
 .
.
 – средняя кривизна поверхности в заданной точке.
– средняя кривизна поверхности в заданной точке.
В нашем случае:
 . (10)
. (10)
 . (11)
. (11)
 .
.

Можно считать, что
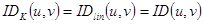
Тогда:  .
.
Аналогичная величина для произвольной линейчатой поверхности имеет вид:
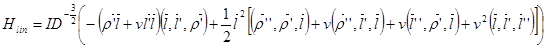
Как мы видим, – последнее слагаемое обращается в нуль  .
.
Очевидно, что для поверхности Каталана:
 .
.
Подставим это выражение для  ,
,  ,
, 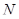 для поверхности Каталана.
для поверхности Каталана.
Итак, пересчитаем коэффициенты второй квадратичной формы для поверхности Каталана.
 (12)
(12)
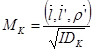 - без изменений
- без изменений
 – без изменений.
– без изменений.
Теперь средняя кривизна.
 (13)
(13)
Попробуем найти все минимальные поверхности Каталана.


 (14)
(14)
Рассмотрим два случая.
1. Поверхность Каталана является развертывающейся поверхностью (т.е. цилиндром).
Тогда, очевидно:  ,
,  .
.
Уравнение примет вид:
 . (15)
. (15)
Пусть  . Также, можно положить
. Также, можно положить 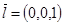 . Тогда уравнение запишется в виде:
. Тогда уравнение запишется в виде:
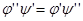 (16)
(16)
Предположим, что функция  известная (ситуация абсолютно симметрична, как мы видим).
известная (ситуация абсолютно симметрична, как мы видим).

Сделаем замену искомой функции:
 . Получим:
. Получим:

Предположим, что  . Быть может за исключением какого-то множества точек, которое мы исключим из рассмотрения (так как нас интересуют общие, регулярные свойства поверхности, то на общность рассмотрения это не повлияет).
. Быть может за исключением какого-то множества точек, которое мы исключим из рассмотрения (так как нас интересуют общие, регулярные свойства поверхности, то на общность рассмотрения это не повлияет).
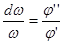
 .
.
Далее: 
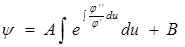 .
.
Таким образом, все цилиндры вида:
 (17)
(17)
являются минимальными поверхностями.
Заметим, что
 , поэтому.
, поэтому.

Также может выполняться, если 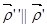 , т.е. если
, т.е. если  , то выполняется система:
, то выполняется система:

причем  (нигде, кроме быть может, каких-то точек). Проинтегрируем, например первое уравнение.
(нигде, кроме быть может, каких-то точек). Проинтегрируем, например первое уравнение.

Сделаем замену искомой функции:  .
.
Получим:

 .
.

 .
.
Откуда  .
.
В результате получаем более приемлемое выражение, описывающее все минимальные цилиндры (с точностью до ориентации в пространстве).
Пусть для удобства записи функция
 , тогда:
, тогда:  .
.
Итак, цилиндры, вида:

являются минимальными поверхностями.
Однако, как легко видеть – это только плоскости…
Теорема 3.1. О минимальных цилиндрах.
Среди цилиндров только плоскости являются минимальными поверхностями.
Доказательство
Пусть дан цилиндр.
 ,
,
 ,
,
 ,
,

 ,
,
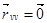
Тогда  ,
,

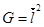 ,
,
 ,
,
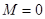 ,
,
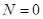
Поэтому уравнение для определения главных кривизн
 ,
,
примет вид.

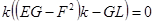 , т.е.
, т.е.


Вспомним формулу для средней кривизны, а именно:

В нашем случае, это возможно только если  . А это означает, что цилиндрическая поверхность сплошь состоит из точек уплощения. Т.е. является плоскостью.
. А это означает, что цилиндрическая поверхность сплошь состоит из точек уплощения. Т.е. является плоскостью.
Вернемся к рассмотрению уравнения (14)


Рассмотрим случай, когда  (т.е. поверхность Каталана является косой линейчатой поверхностью).
(т.е. поверхность Каталана является косой линейчатой поверхностью).
Улучшений здесь не видно, особенно.
Рассмотрим один специальный случай:  .
.
Т.е. 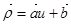 ,
, 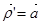 .
.
Получим:
 ,
,
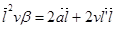
Теорема 3.3. О минимальных поверхностях Каталана.
Если имеет место разложение:  для поверхности Каталана
для поверхности Каталана  , то она является минимальной, если верно уравнение
, то она является минимальной, если верно уравнение

Рассмотрим пример минимальной поверхности Каталана.
 .
.
Это прямой архимедов геликоид. Т.е.
 ,
,
 ,
,
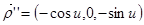 ,
,
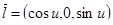 ,
,
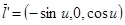 ,
,
 .
.
Имеет место разложение:
 , т.е.
, т.е.
 ,
,  .
.
 ,
,
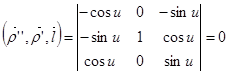 ,
,
 ,
,
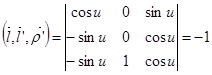 ,
,
 ,
,
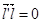
 , получим
, получим  .
.
Действительно, прямой архимедов геликоид – минимальная поверхность Каталана.
Еще раз напомним, как он выглядит.

О коноидах
Выведем условие, при котором поверхность Каталана будет являться коноидом.
Т.е. задана поверхность Каталана
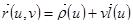 .
.
Определим, когда есть прямая, пересекающая все образующие данной поверхности.
Пусть есть кривая на этой поверхности:

Причем она не совпадает ни с одной из образующих, т.е.  .
.
Уравнение этой кривой в пространстве имеет вид:

Если в каждой точке кривизна равно нулю – то это связное множество точек, которое лежит на прямой.
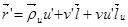 .
.
 .
.
Рассмотрим векторное произведение:

Как мы видим, это не очень удобная запись. Попробуем использовать соотношение:


Сгруппируем члены при векторах.
 (18)
(18)
Умножим это равенство векторно на  справа.
справа.

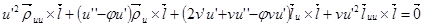
А теперь умножим скалярно на 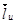 .
.

Так как мы рассматриваем поверхности Каталана, то  . В результате получим.
. В результате получим.
 (19)
(19)
Дифференциальное уравнение (19) дает необходимое условие того, чтобы поверхность Каталана являлась коноидом.
Рассмотрим специальный простой случай, а именно, когда поверхность Каталана является цилиндром (  ) в этом случае уравнение (19) примет вид:
) в этом случае уравнение (19) примет вид:  . Т.е. вырождается. Это и понятно, поскольку мы делали неравносильные преобразования уравнения, а выводили следствия путем соответствующих преобразований.
. Т.е. вырождается. Это и понятно, поскольку мы делали неравносильные преобразования уравнения, а выводили следствия путем соответствующих преобразований.
И действительно:
Если имеется равенство:  , очевидно, что если его справа или слева умножить векторно на какой-то вектор, то оно сохраниться. Например:
, очевидно, что если его справа или слева умножить векторно на какой-то вектор, то оно сохраниться. Например:
 .
.
Однако из этой записи вышеуказанное равенство не следует. Ибо если  , то это тождество… Аналогично со скалярным произведением… А если
, то это тождество… Аналогично со скалярным произведением… А если  то
то  , а мы как раз умножали скалярно на
, а мы как раз умножали скалярно на  . Отсюда и вырождение уравнения…
. Отсюда и вырождение уравнения…
Очевидно, мы пока не получили достаточно удовлетворительного уравнения для характеризации коноидов среди линейчатых поверхностей. Воспользуемся тем фактом, что для прямой верно, что  , и обратно, если для кривой этой выполняется, – то она прямая. Это справедливо в силу того, что параметрическое уравнение прямой:
, и обратно, если для кривой этой выполняется, – то она прямая. Это справедливо в силу того, что параметрическое уравнение прямой:
 ,
, 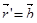 .
.
Итак 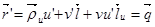 (20)
(20)
Рассмотрим снова два случая.
1.  . Т.е. поверхность Каталана является цилиндром. В таком случае:
. Т.е. поверхность Каталана является цилиндром. В таком случае:
 (21)
(21)
Т.е. если уравнение (21) в указанных в начале продолжениях имеет решение, то оно определяет параметрическое уравнение прямой, через которую проходят все образующие цилиндра.
Умножим уравнение справа на  векторно.
векторно.
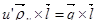 .
.
Откуда очевидно, что:
 (22)
(22)
Рассмотрим уравнение (22) для какой-нибудь одной координаты. Пусть
 ,
,  .
.


 .
.
Другими словами:
 .
.
Возвращаясь к уравнению  и имея в виду:
и имея в виду:  , получим, что
, получим, что 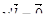 , а значит,
, а значит,  .
.
Т.е. всякий цилиндр является коноидом, если существует такая функция  , что
, что
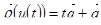 ,
,
при этом, общая прямая, через которую проходят все образующие цилиндра имеет вид:
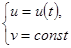
Естественно – это целое семейство прямых.
Попробуем сразу воспользоваться найденным приемом для уравнения (21).

Это можно переписать так:
 ,
,

 (23)
(23)
Откуда также можно сделать вывод, что  – иначе равенство невозможно. Также, очевидно, что и
– иначе равенство невозможно. Также, очевидно, что и 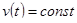 . Другими словами существует такая замена переменного параметра
. Другими словами существует такая замена переменного параметра 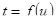 , что выполнится указанное выше соотношение.
, что выполнится указанное выше соотношение.
Если проанализировать это равенство для одной из координат:
 .
.
Тогда, если существует обратная функция  , то:
, то:
 .
.
Проверим наши выкладки на примере.
Рассмотрим два цилиндра:
1) 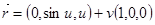

Проверим, является ли этот цилиндр коноидом:
 .
.
Допустим, что локально можно положить:

С другой стороны,
 .
.
Естественно, выполнение этих двух условий в системе возможно только в каких-то определенных точках, что нас не устраивает. Очевидно, это не коноид. Результат тем более очевиден, что если  , то лини
, то лини  – это синусоиды, а не прямые.
– это синусоиды, а не прямые.
2)  .
.
Очевидно:
 ,
,
остальные равенства выполняются при равенстве нулю коэффициентов линейной функции.
Очевидно, что коэффициенты в данном случае влияют лишь на динамику обхода линий  .
.
Данная поверхность Каталана является коноидом.
Итак, данный цилиндр, является коноидом, тогда и только тогда, когда существует такая замена переменного  , что
, что
 . (24)
. (24)
При этом найдется целое семейство прямых, каждый член которого не совпадет ни с одной образующей и который все образующие пересекают.
Из (24) легко понять, что если такая замена существует, то поверхность является просто плоскостью. Другими словами, справедлива теорема.
Теорема 3.2.О кониодных цилиндрах.
Среди всех цилиндров только плоскость является коноидом.
Вернемся к рассмотрению общего случая соотношения (20). Напомним.

Перепишем это уравнение в следующем виде:


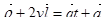
Константу можно «убрать» в функцию  .
.
 .
.
Рассмотрения возможных случаев, когда данное уравнение имеет невырожденное решение мы оставим за границами нашего рассмотрения.
|
из
5.00
|
Обсуждение в статье: Первая и вторая квадратичные формы поверхности Каталана |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

