Классификация точек регулярной поверхности

 

Пусть  – регулярная поверхность и  – ее параметрическое задание.

Выберем на поверхности  некоторую точку  и рассмотрим плоскость , которая касается поверхности  в этой точке.

Отклонение произвольной точки 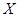 поверхности  от плоскости  определим по формуле

 

                                                                                 (1)

 

В этой формуле  – единичный вектор нормали к поверхности в точке . Это отклонение, взятое по абсолютной величине, равно расстоянию от точки  до плоскости . Отклонение положительно, если точка 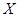 и конец вектора  лежат по одну сторону от касательной плоскости, соответственно, оно отрицательно, если они лежат по разные стороны от касательной плоскости в точке .

Рассмотрим формулу (1).

Разность  допускает следующую интерпретацию

 

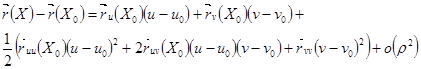                      (2)

Где

 

, при .

 

Умножим обе части равенства (2) скалярно на вектор  и положив

 

, .

 

Получим, что

 

                                                      (3)

 

Разумеется, вдумчивый (или хотя бы немного читающий эти выкладки) читатель поймет, что коэффициенты

,

,

 

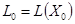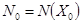
указанные в формуле (3) вычислены в точке , в окрестности которой мы и рассматриваем исходную поверхность .

Из курса линейной алгебры известно, что свойства квадратичной формы во многом определяются ее дискриминантом. А скорее даже знаком квадратичной формы.

Вычислим дискриминант второй квадратичной формы в точке .

 

 

Рассмотрим все возможные случаи.([7],[8],[9],[10],[11])

Случай 1.

 

 

Т.е. вторая квадратичная форма поверхности в заданной точке является знакоопределенной.

Зафиксируем в точке  некоторое направление на поверхности. Пускай .

Тогда любое другое направление на поверхности в точке  можно задавать при помощи угла , который оно образует с уже выбранным направлением.

Положим

 

,

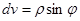
Тогда

 

                                             (4)

 

Нетрудно показать, что

 

,

 

где постоянная

 

 

а в силу условия

 положительна.

Таким образом неравенство

 

 

выполняется независимо от выбора угла .

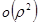Так как порядок стремления к нулю при  второго слагаемого  в правой части формулы (3) выше двух, то из последней оценки можно сделать следующий вывод.

Отклонение  сохраняет знак (совпадающий со знаком второй квадратичной формы ) для всех достаточно малых значений независимо от выбора направления на поверхности.

Это означает, что все точки поверхности , достаточно близкие к точке , располагаются по одну сторону от касательной плоскости поверхности в этой точке. Такая точка поверхности называется эллиптической точкой.

Например, все точки сфер – эллиптические.([6],[8])

 

 

Случай 2.

 

.

 

Вторая квадратичная форма является знакопеременной.

Покажем, что в этом случае, в точке  можно указать два неколлинеарных направления на поверхности, обладающие следующими свойствами:

- для значений дифференциалов, определяющих эти направления, вторая квадратичная форма поверхности, вычисленная в точке , обращается в нуль,

- все остальные направления на поверхности в точке  разбиваются на два класса – для дифференциалов, определяющих направления одного из этих классов, вторая квадратичная форма положительна и для другого отрицательна.

Пусть некоторое направление  положительного класса задается углом . В соответствии с формулой (4) имеем

 

, ([1],[4],[11])

где

Как видно из формулы (3), знак отклонения  для всех достаточно малых значений  в рассматриваемом направлении  совпадает со знаком второй квадратичной формы . Следовательно, если точка  поверхности  достаточно близка к точке , то это отклонение положительно.

Рассуждая аналогично, можно указать точки на поверхности, близкие к точке , для которых отклонение  будет отрицательным.

Приведенные рассуждения показывают, что вблизи точки  поверхность  располагается по разные стороны от касательной плоскости. При этом проекции точек поверхности, отклонения которых расположены на касательный плоскости заполняются множество «между» этими направлениями…

В этом случае точка называется гиперболической точкой поверхности.

 

 

Случай 3.

 

.

 

Но отличен от нуля хотя бы один из коэффициентов, , .

Пусть для определенности . Тогда вторая квадратичная форма поверхности  в точке  может быть записана в следующем виде

 

Тем самым в зависимости от знака  форма  либо неотрицательна, либо неположительна. При этом на поверхности  в точке  можно указать направление , такое, что определяющие его дифференциалы  и  обращают вторую квадратичную форму  в нуль.

Для всех других направлений на поверхности в точке  форма имеет один и тот же знак (совпадающий со знаком )

 

 

В этом случае точка  называется параболической точкой поверхности .

Случай 4. ([1],[11],[12])

 

 

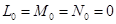
Такая точка  называется точкой уплощения поверхности. Расположение поверхности, близ таких точек может быть самым разнообразным.

Например, все точки плоскости являются точками уплощения.