II.4 Квантование электронов в квантовых ямах

 

Рассмотрим электрон в КЯ типа I, образованной двумя полупроводниками с похожими параболическими зонами проводимости. Кроме того, предположим, что направление роста (ось z) параллельно одной из главных осей тензора эффективной массы в обоих материалах. Энергии и волновые функции электрона могут быть вычислены в приближении эффективной массы, если ширина ямы много больше толщины одного монослоя. Обозначим функции Ванье и огибающие функции внутри ямы через а_nA и C_nA, а соответствующие функции в барьере - через а_nB и C_nB. Рассматриваемое приближение часто называют приближением огибающих функций. Волновую функцию электрона в КЯ можно представить в виде

 

 

 

 

 

 

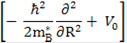
^-1/2∑C_nA (R_i) a_nA (r - R_i) при - L/2 ≤ z ≤ L/2,

Ψ(r) = (II.5)

N^-1/2∑C_nB (R_i) a_nB (r - R_i) при z > L/2 или z <−L/2,

 

Уравнения движения для огибающих функций также различны внутри и вне ямы.

Для изотропных эффективных масс (m*_A и m*_B для ям и барьеров соответственно) эти уравнения имеют вид

_A (R) ≈ [E - E_cA] C_A(R) при −L/2 ≤ z ≤ L/2 (II.6а)

C_B (R) ≈ [E - E_cA] C_B(R)

при z > L/2 или z <−L/2/, (1.6б)

 

где Е_са - край зоны проводимости в яме (без ограничения общности он будет принят равным нулю).

Поскольку потенциал ямы зависит только от z, можно разделить (II.6 а) и (II.6б) на два уравнения, из которых одно будет зависеть только от z, а другое - только от x и у. После этого можно выразить волновые функции С _{(А или В)} (x, y, z) в виде произведения решений этих двух уравнений:

 

 

 

 

C_{(A или B)} (x, y, z) = 𝜙_{(A или B)} (x, y) 𝜓_{(A или В)} (z). (II.7a)

 

Выражение для 𝜙_{(A или B)} (x, y) является уравнением для свободной частицы, и поэтому его решения представляют собой плоские волны вида

 

𝜙_{(A или B)} (x, y) ∝ exp [ i (k_xx + k_yy)] (II.7б)

 

где к_х и к_у - компоненты блоховских волновых векторов, параллельных плоскости ямы. Поскольку в плоскости ху сохраняется трансляционная инвариантность, все теоремы, касающиеся сохранения к и полученные для объемных кристаллов, применимы к к_х и к_у, но не применимы к z-компоненте.

Отметим, что масса изменяется от значения т_А^* внутри ямы до значения m^*_В вне ее. Однако из граничного условия о непрерывности волновых функций по обе стороны интерфейса следует, что как к_х, так и к_у должны быть одними и теми же внутри и вне ямы. Уравнения для 𝜓_{(A или В)} (z)имеют вид :

 

при - L/2 ≤ z ≤ L/2 (II.8а)

при z > L/2 или z < - L/2. (II.8б)

 

За исключением того, что массы m_А^* и m^*_В могут различаться, выражения (II.8) при к_х = к_у = 0 идентичны случаю частицы, находящейся в одномерной прямоугольной яме.

В общем случае (II.8) имеет два типа решений. Если Е - [ℏ²/(2 m^*_В )]( k_x² +k²_y) > V_o, то решения являются плоскими волнами с непрерывным спектром энергий. Частица обладает достаточной кинетической энергией для преодоления барьера и поэтому не испытывает конфайнмента в яме. И если Е - [ℏ²/(2 т_А^*)](k_x² +k²_y ) < V₀, то решения (1.8 6) являются экспоненциальными функциями вида

 

 

 

 

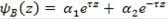 (II.9а)

 

где 𝜏 - положительное реальное число, которое находится из уравнения

 

 

(II.10)

 

Из условия конечности 𝜓_B(z) при z = ± ∞ следует

 

𝛼₁e^𝜏z при z <- L/2

𝜓_B(z) = (II.9б)

𝛼₂e-^𝜏z при z > L/2

 

Волновая функция 𝜙_B(x, y) 𝜓_В(z) описывает волну, распространяющуюся параллельно яме, но экспоненциально затухающую в барьерах по мере удаления от интерфейсов.

Такие волны называются затухающими волнами. Их волновой вектор имеет мнимую z - компоненту, равную ±i𝜏.

Внутри ямы решения (1.8 а) могут быть представлены в виде линейной комбинации симметризованных волновых функций (по отношению к отражению в плоскости z = 0), таких как косинус (симметричная функция) и синус (антисимметричная функция):

 

𝜓_A(z) = 𝛽₁cos (k_z z) или 𝛽₂sin (k_z z) для - L/2 < z < L/2 (II.9в)

 

В рассматриваемом случае разрешенные значения Е имеют дискретный характер. Эти решения, описывающие связанные состояния, (т.е. четыре коэффициента 𝛼₁, 𝛼₂ , 𝛽₁ и 𝛽₂) определяются путем наложения обычного требования: волновые функции и их первые производные должны быть непрерывны при пересечении двух интерфейсов КЯ. Обычно не существует аналитического выражения для собственных значений, за исключением случая, когда V₀ - бесконечная величина. Тогда частица полностью заперта внутри ямы (и поэтому значения m^*_В не существенны), а значения k_z даются классическими выражениями для стоячих волн:

 

 

k_z = n𝜋/L, где n=1, 2, 3… (II.11)

 

Соответствующие энергии имеют вид

 

 

E_n (k_x, k_y)= , n= 1,2,3… (II.12a)

 

При к_х = к_у = 0 уровни энергии равны (II.12б)

 

Рис. II.5.

На рис. II.5 показаны уровни энергии электронов в КЯ с бесконечными барьерами. Эти энергетические зоны, квантованные в двух измерениях, называют подзонами, чтобы отличать их от электронных энергетических зон соответствующего объемного кристалла А.

При конечном значении V₀ энергии подзон не могут быть выражены аналитически. Их можно определить или графически, или посредством численных расчетов с помощью компьютера. При m*_А ≠ m^*_В условие непрерывности для производных 𝜕𝜓_А(z)/𝜕z и 𝜕𝜓_В(z)/𝜕z следует преобразовать в так называемое граничное условие Бастарда:

 

при z = ± L/2 (II.13)

 

Оно обеспечивает непрерывность потока частиц через интерфейс между А и В.

На рис. II.6 показана зависимость вычисленных энергий связанных состояний электрона (для к_х = к_у = 0) от ширины L ямы в КЯ Ga_0,47In_0,53As - Al_0,48In_0,52As. Глубина ямы V₀ = 0,5 эВ. Число связанных состояний внутри ямы уменьшается по мере уменьшения L. Для L < 30 А существует только одно связанное состояние. Непрерывные, или «несвязанные», решения модифицируются потенциалом ямы и отличаются от соответствующих состояний в объемных кристаллах.

 

 

 

Рис. II.6.