Аналитическая оценка уравнения тренда. Методика прогнозирования уравнения ряда динамики

Наличие либо отсутствие тренда часто хорошо видно на графике. Проверку этой гипотезы в сомнительных случаях можно осуществить с использованием некоторых простых критериев, широко описанных в литературе по статистике.

Тест числа поворотных точек основан на вычислении числа локальных максимумов. Отклонение этого числа от идеального значения в большую сторону свидетельствует о значительной дисперсии и заметной отрицательной автокорреляции случайной компоненты. Отклонение в меньшую сторону может возникнуть как при наличии тренда, так и в случае положительной автокорреляции (первого порядка) случайной компоненты. Последняя ситуация возникает и для стационарных рядов.

Критерий знаков разности чувствителен как к наличию тренда, так и к присутствию квазипериодической компоненты. Случайная компонента мало сказывается на результаты тестирования с использованием этого критерия.

Критерий ранговой корреляции Кендала является хорошим тестом на наличие монотонного или кусочно-монотонного тренда для не очень длинных рядов. Положительный коэффициент соответствует возрастающему тренду, отрицательный - убывающему.

Критерий ранговой корреляции Спирмена по своему смыслу и свойствам близок к коэффициенту Кендала.

Параметрические модели тренда

Для коротких временных рядов наиболее употребительны параметрические методы выделения тренда. В этом случае делается попытка представить временной ряд в виде суммы детерминированной функции времени f (t, a), зависящей от небольшого числа неизвестных параметров, и случайной компоненты. Для оценки вектора неизвестных параметров a обычно применяется метод наименьших квадратов (МНК), состоящий в минимизации суммы квадратов отклонений

 

[x(t) - f (t, a)] 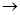min.

 

Нет необходимости приводить здесь описание методологии МНК и расчетных формул применительно к линейному и нелинейному регрессионному анализу, поскольку все это доступно практически в любом руководстве по математической статистике. Остается лишь предостеречь от от популярных, к сожалению, приемов необоснованной «линеаризации», т.е. использования линейного формализма МНК для расчета коэффициентов уравнения в той или иной нелинейной форме. Например, для расчета коэффициентов экспоненциального уравнения регрессии часто логарифмируют исходные данные, после чего используют формулы МНК для коэффициентов линейного уравнения, получая при этом заведомо искаженные результаты. Минимизация суммы квадратов отклонений между уровнями ряда и прогнозируемыми значениями, вычисленными по нелинейным уравнениям связи, в настоящей работе проводилась по методу Нелдера-Мида, реализующему прямой поиск по деформируемому многограннику. [14]

Традиционной проблемой является выбор наилучшего вида модели тренда. В качестве такого критерия отбора может быть использована доля объясненной дисперсии, называемая коэффициентом детерминации:

 

где - дисперсия остатков; 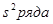- дисперсия исходного ряда.

Непосредственная оценка коэффициента детерминации по приведенной формуле через выборочные дисперсии приводит к смещенной оценке, поэтому для построения несмещенной оценки вводится поправочный коэффициент, учитывающий число оцениваемых параметров. Получающийся при этом коэффициент называют скорректированным коэффициентом детерминации:

 

 

где n - число наблюдений; k - число оцениваемых параметров (или число независимых переменных). В отличие от коэффициента , значение которого при включении в регрессионную модель дополнительной независимой переменной может лишь возрасти, коэффициент  может и уменьшиться, если снижение дисперсии остатков оказалось менее существенным по сравнению с ростом числа оцениваемых параметров.

Удобным средством описания одномерных временных рядов является их выравнивание с помощью тех или иных функций времени (кривых роста). Кривая роста позволяет получить теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.

Аппроксимация, или приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.

Алгоритм прогнозирования с использованием кривых роста приведен на рис. 1.

В настоящее время известно несколько десятков кривых роста, многие из которых широко применяются для выравнивания экономических временных рядов.

Кривые роста условно могут быть разделены на три класса в зависимости от того, какой тип динамики развития они хорошо описывают.

. Функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей, например, для большинства натуральных показателей промышленного производства.

. Кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. С такими процессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при исследовании эффективности использования ресурсов и т.д.

Примерами показателей, для которых могут быть указаны пределы роста, являются среднедушевое потребление определенных продуктов питания, расход удобрений на единицу площади и т.п.

Функции, относящиеся ко II классу, называются кривыми насыщения.

. Если кривые насыщения имеют точки перегиба, то они относятся к III типу кривых роста - к S-образным кривым. Эти кривые описывают как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, другой - с замедлением.

S-образные кривые находят применение в демографических исследованиях, в страховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции.

Вопрос о выборе кривой является основным при выравнивании ряда. Существует несколько подходов к решению этой задачи, однако, все они предполагают анализ основных свойств используемых кривых роста.

Рассмотрим порядок аппроксимации временных рядов с помощью полиномов, которые относятся к кривым I типа:

 

 (1)

 

где aк (к = 0,1,…, p) - параметры многочлена,

t - независимая переменная (время).

Коэффициенты полиномов невысоких степеней могут иметь конкретную интерпретацию в зависимости от содержания динамического ряда. Например, их можно трактовать как скорость роста (a1), ускорение роста (a2), изменение ускорения (a3), начальный уровень ряда при t = 0 (a0).

Обычно в экономических исследованиях применяются полиномы не выше третьего порядка. Использовать для определения тренда полиномы высоких степеней нецелесообразно, поскольку полученные таким образом аппроксимирующие функции будут отражать случайные отклонения (что противоречит смыслу тенденции).

Полином первой степени  на графике изображается прямой и используется для описания процессов, развивающихся во времени равномерно.

Полином первого порядка (прямая)

 

Полином второй степени применим в тех случаях, когда процесс развивается равноускоренно (т.е. имеется равноускоренный рост или равноускоренное снижение уровней). Как известно, если параметр a2 > 0, то ветви параболы направлены вверх, если же a2 < 0, то вниз. Параметры a0 и a1 не влияют на форму параболы, а лишь определяют ее положение.

 

Полином второго порядка (парабола)

 

Полином третьей степени имеет вид . У этого полинома знак прироста ординат может изменяться один или два раза, то есть такая кривая имеет точку перегиба.

Отличительная черта полиномов - отсутствие в явном виде зависимости приростов от значений ординат.

Оценки параметров моделей определяются методом наименьших квадратов. Суть этого метода состоит в том, что выбирается такая модель и такие ее параметры, при которых сумма квадратов отклонений расчетных значений уровней от фактических значений будет минимальной. Таким образом, оценки параметров кривой роста находятся в результате минимизации функции:

 

, (2)

 

где 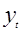 - фактическое значение временного ряда в момент времени t;

 - расчетное (теоретическое) значение временного ряда в момент времени t;

n - длина временного ряда.

Существует ряд модификаций метода наименьших квадратов, подробно описанного в литературе по математической статистике.

В результате минимизации выражения (2) строится система нормальных уравнений. Система состоит из (p+1) уравнений, содержащих в качестве неизвестных величин (p+1) коэффициентов . Решение этой системы позволяет вычислить оценки искомых коэффициентов (параметров) моделей. [15]

Оценивание параметров моделей

Система нормальных уравнений для оценивания параметров прямой состоит из двух уравнений:

 (3)

 

Для параболы второго порядка система содержит три уравнения, позволяющих найти оценки трех неизвестных коэффициентов :

 

 (4)

 

Существует подход к упрощению расчетов, который заключается в переносе начала координат в середину ряда динамики. Это позволяет упростить сами нормальные уравнения, а также уменьшить абсолютные значения величин, участвующих в расчете.

Если до переноса начала координат t было равно1,2,3,…,

то после переноса:

для четного числа членов ряда t =…, - 5; -3; -1; 1; 3; 5;…;

для нечетного числа членов ряда t =…, - 3; -2; -1; 0; 1; 2; 3;….

После переноса начала координат сумма нечетных степеней ,

что существенно упрощает систему нормальных уравнений.

В этом случае оценки параметров соответствующих полиномов имеют находятся из соотношений:

Прямая:

 

; (5)

Парабола:

 

. (6)

 

Для прогнозирования на базе полученной модели на k шагов вперед необходимо в уравнение кривой роста подставить соответствующее значение временного параметра t, т.е. tпр = tn + k, учитывая номер временной точки при переносе шкалы времени в середину координат. Если оценки коэффициентов модели были получены без переноса начала координат в середину ряда, то следует подставить в модель значение временного параметра t, равного реальному прогнозному значению. [16]

Прогнозирование по методу экспоненциальных средних

В настоящее время одним из наиболее перспективных направлений исследования и прогнозирования одномерных временных рядов являются адаптивные методы.

При обработке временных рядов, как правило, наиболее ценной является информация последнего периода, т.к. необходимо знать, как будет развиваться тенденция, существующая в данный момент, а не тенденция, сложившаяся в среднем на всем рассматриваемом периоде. Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, степень «устаревания» данных.

Прогнозирование методом экстраполяции на основе кривых роста в какой-то мере тоже содержит элемент адаптации, поскольку с получением «свежих» фактических данных параметры кривых пересчитываются заново.

Поступление новых данных может привести и к замене выбранной ранее кривой на другую модель. Однако степень адаптации в данном случае весьма незначительна, кроме того, она падает с ростом длины временного ряда, т.к. при этом уменьшается «весомость» каждой новой точки. В адаптивных методах различную ценность уровней в зависимости от их «возраста» можно учесть с помощью системы весов, придаваемых этим уровням.

Оценивание коэффициентов адаптивной модели обычно осуществляется на основе рекуррентного метода, который формально отличается от метода наименьших квадратов, метода максимального правдоподобия и других методов тем, что не требует повторения всего объема вычислений при появлении новых данных. [17]

Примером простейшей адаптивной модели является экспоненциальная средняя. Экспоненциальное сглаживание временного ряда производится итеративно (пошагово), причем массив прошлой информации представлен единственным значением сглаженного уровня ряда в предыдущий момент времени.

Для экспоненциального сглаживания ряда используется рекуррентная формула:

 

, (7)

 

где S_t - значение экспоненциальной средней в момент t;

α - параметр сглаживания, α =сonst, 0< α <1;

 

β = 1 - α.

 

Если последовательно использовать соотношение (7), то экспоненциальную среднюю S_t можно выразить через предшествующие значения уровней временного ряда. При

. (8)

 

Таким образом, величина S_t является взвешенной суммой всех членов ряда. При этом, веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от «возраста» наблюдений). Поэтому величина S_t названа экспоненциальной средней.

Английский математик Р. Браун показал, что дисперсия экспоненциальной средней D[S_t] меньше дисперсии временного ряда :

 

. (9)

 

Следует, что при высоком значении α дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением α дисперсия экспоненциальной средней уменьшается, возрастает ее отличие от дисперсии ряда. Тем самым, экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного ряда.

Таким образом, с одной стороны, необходимо увеличивать вес более свежих наблюдений, что может быть достигнуто повышением α, с другой стороны, для сглаживания случайных отклонений величину α нужно уменьшить.

Эти два требования находятся в противоречии. Поиск компромиссногозначения параметра сглаживания α составляет задачу оптимизации модели.

Часто поиск оптимального значения α осуществляется путем перебора и в качестве оптимального выбирается такое значение, при котором получена наименьшая дисперсия ошибки. Обычно параметр сглаживания принимается равным в интервале от 0,1 до 0,3.

При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда имеет вид: y_t = a_1,t + e_t, где a_1,t - варьирующий во времени средний уровень ряда, e_t - случайные не автокоррелированные отклонения с нулевым математическим ожиданием и дисперсией .

Прогнозная модель определяется равенством

 

,

 

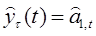где  - прогноз, сделанный в момент t на τ единиц времени (шагов) вперед; - оценка параметра в момент времени t.

Единственный параметр модели â_1,t определяется экспоненциальной средней: â _1,1 = S_t; â _1,0 = S_0.

Выражение (7) можно представить иначе:

 

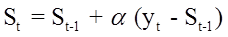. (10)

 

Величину  можно рассматривать как погрешность прогноза. Тогда новый прогноз S_t получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.

Экспоненциальное сглаживание является примером простейшей самообучающейся модели. Массив прошлой информации уменьшен до единственного значения S_t-1. [18]