Термодинамика нелинейных систем. Проблемы исследования нелинейных систем

              1. Проблемы исследования нелинейных систем

              2. Вторая вариация энтропии многофазной гетерогенной среды

              3. Исследование знака второй вариации энтропии

              4. Производная второй вариации энтропии. Термодинамический анализ

              5. Осцилляторы при кристаллизации малорастворимых веществ

                          5.1. Представления Оствальда об образовании периодических структур

                          5.2. Кристаллизация малорастворимых веществ

                          5.3. Механизм кристаллизации малорастворимых веществ

                          5.4. Примеры образования диссипативных структур при кристаллизации

                          5.5. Выражение для избыточного производства энтропии

                          5.6. Анализ причин образования диссипативных структур

1. Проблемы исследования нелинейных систем

Линейная неравновесная термодинамика описывает стабильное, предсказуемое поведение систем, стремящихся к минимальной активности в соответствии с питающими их внешними потоками. Из того, что линейная термодинамика допускает описание с помощью потенциала (а именно, производства энтропии), следует: при эволюции к равновесию или к стационарному состоянию система “забывает” начальные условия. Каковы бы ни были начальные условия, система рано или поздно перейдёт в состояние, определяемое граничными условиями. В результате реакция такой системы на любое изменение граничных условий становится предсказуемой.

Таким образом, в линейной области (т.е. в области применимости соотношений Онзагера) ситуация остаётся такой же, как и в равновесной. В нелинейной области (при достаточном удалении от равновесия), т.е. когда термодинамические потоки уже более не являются линейными функциями термодинамических сил, ситуация коренным образом меняется. Несмотря на все попытки обобщение теоремы о минимуме производства энтропии на нелинейные системы оказалось невозможным [4]. Вдали от равновесия система по-прежнему может эволюционировать к некоторому стационарному состоянию, но это состояние уже не определяется с помощью надлежаще выбранного потенциала.

В связи с этим возникает вопрос: что можно сказать относительно устойчивости состояний, к которым эволюционирует нелинейная система? До тех пор пока состояние определяется минимумом потенциала (производства энтропии), его устойчивость гарантирована. Флуктуации могут вывести систему из этого минимума, но второе начало термодинамики вынудит её вернуться обратно. Таким образом, существование термодинамического потенциала делает систему невосприимчивой к флуктуациям. Располагая потенциалом, мы описываем стабильный мир, в котором системы, эволюционируя, переходят в статичное состояние, установленное для них раз и навсегда. Но когда термодинамические силы, действуя на систему, становятся достаточно большими и вынуждают её покинуть линейную область, гарантировать устойчивость стационарного состояния или его независимость от флуктуаций невозможно. За пределами линейной области устойчивость уже не является следствием общих законов физики. Необходимо специально изучать, каким образом стационарное состояние реагирует на различные типы флуктуаций, создаваемых системой или окружающей средой.

Неравновесная термодинамика не даёт ответа на вопрос, каким образом происходит потеря устойчивости прежнего состояния и переход к новому, но она позволяет выяснить, какие причины побуждают систему к этому переходу.

2. Вторая вариация энтропии многофазной гетерогенной среды

Согласно второму началу термодинамики (1.1) состояние равновесия изолированной системы устойчиво, если оно соответствует максимуму энтропии. Энтропию системы, находящейся вблизи равновесного состояния, можно представить в виде:

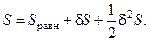                                                                                (5.1)

Здесь 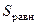 – значение энтропии в состоянии равновесия;  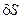и 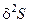 – первая и вторая вариации энтропии системы. Под вариацией какого-либо параметра Y понимают отклонение величины этого параметра от его стационарного или равновесного значения  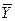под воздействием внешних возмущений:

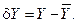
Поскольку 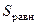 является максимальным значением энтропии, член первого порядка  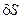обращается в нуль, и следовательно, устойчивость состояния системы, находящейся вблизи равновесия, определяется знаком члена второго порядка 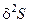. Таким образом, в области, близкой к равновесию,  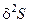играет роль функции Ляпунова.

Для многофазной гетерогенной среды, в которой могут происходить химические и фазовые превращения, вторая вариация энтропии имеет вид:

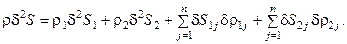
Здесь 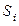 – удельная энтропия i-й фазы (i = 1,2);  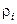– средняя плотность i-й фазы;  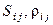– энтропия и средняя плотность j-го компонента в i-й фазе.

С помощью ряда преобразований [6], это выражение можно представить в виде квадратичной формы:

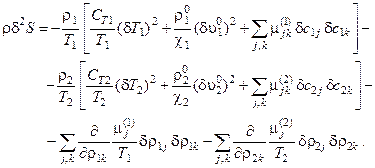                       (5.2)

Здесь 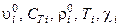 – удельный объём, теплоёмкость, истинная плотность, температура и коэффициент сжимаемости i-й фазы (i = 1,2), соответственно;  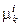– химический потенциал k-го компонента в i-й фазе;

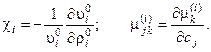
3. Исследование знака второй вариации энтропии

Вторая вариация энтропии физико-химической системы (5.2) в окрестности состояния равновесия отрицательна:

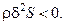
Для справедливости этого неравенства требуется выполнение следующих условий:

· условие тепловой устойчивости в фазах

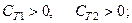                                                                                    (5.3)

· условие механической устойчивости

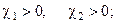                                                                                        (5.4)

· условие устойчивости по отношению к диффузии в фазах

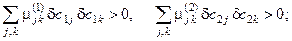                                            (5.5)

· условие устойчивости равновесия при фазовом переходе

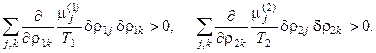                       (5.6)

Каждое из представленных условий имеет физический смысл. Так, если бы нарушилось условие (5.3), то закон Фурье приводил бы не к затуханию, а к усилению небольших флуктуаций температуры в фазах. Неравенство (5.5) означает, что при небольших флуктуациях по концентрациям система стремится восстановить однородность в фазах (т.е., действует закон Фика). В работах [10, 11] доказано, что если система устойчива по отношению к диффузии, то все химические равновесия (для случая, когда в системе протекают химические реакции) также устойчивы. Сравнивая неравенства (5.5) и (5.6), легко видеть, что условие устойчивости равновесия при фазовом превращении (5.6) является следствием условия стабильности по отношению к диффузии (5.5).

Таким образом, при выполнении условий (5.3)-(5.6) вторая вариация энтропии системы (5.2) является отрицательно определённой квадратичной формой. Следовательно, согласно выражению (5.1) условия (5.3)-(5.6) служат необходимыми и достаточными условиями устойчивости равновесия и стационарных состояний системы вблизи равновесия. Но как только система удаляется от равновесия, эти условия перестают быть достаточными для устойчивости стационарных состояний   системы.

4. Производная второй вариации энтропии. Термодинамический анализ

Вторая вариация энтропии физико-химической системы (5.2) является функцией Ляпунова для стационарных состояний системы вдали от равновесия, так как в стационарном состоянии она равна нулю 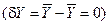, а в его окрестности – является отрицательно определённой квадратичной формой. Следовательно, согласно второму методу Ляпунова для устойчивости стационарного состояния вдали от равновесия необходимо потребовать, чтобы производная термодинамической функции Ляпунова  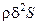имела положительный знак в окрестности этого состояния. В случае совпадения знаков термодинамической функции Ляпунова и её производной исходное стационарное состояние системы становится неустойчивым, и возможно возникновение качественно иного состояния системы.

Производная термодинамической функции Ляпунова (второй вариации энтропии) для гетерогенных систем с химическими и фазовыми превращениями имеет вид [6]:

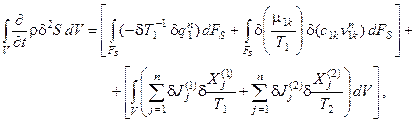             (5.7)

где 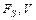 – поверхность и объём системы;  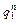– тепловой поток через поверхность системы;  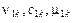– скорость движения, концентрация и химический потенциал k-го компонента в сплошной фазе;  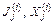– термодинамический поток и термодинамическая движущая сила j-го необратимого процесса в i-й фазе.

Выражение (5.7) по структуре напоминает выражение для изменения энтропии (3.5). Соотношение в первых квадратных скобках характеризует приращение избытка энтропии системы за счёт обмена с окружающей средой энергией и веществом. Соотношение во вторых квадратных скобках характеризует приращение избытка энтропии за счёт внутренних необратимых процессов; по аналогии с термином "производство энтропии" оно было названо избыточным производством энтропии [3].

Таким образом, если

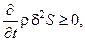
то стационарное состояние системы, находящейся вдали от равновесия, устойчиво, а если

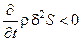
- неустойчиво. Кроме того, рассматривая знаки отдельных слагаемых в выражении (5.7) можно выявить причины, приводящие к потере устойчивости стационарных состояний и возникновению диссипативных самоорганизующихся структур. Анализ устойчивости систем с помощью производной термодинамической функции Ляпунова часто называют термодинамическим анализом.

5. Осцилляторы при кристаллизации малорастворимых веществ

5.1. Представления Оствальда об образовании периодических структур

В большинстве работ, посвящённых явлениям самоорганизации, основное внимание уделяется процессам, происходящим в гомогенных системах. Однако первый колебательный процесс, обнаруженный среди химических реакций, относится к гетерогенным процессам: в 1896 г. В. Лизеганг наблюдал образование концентрических колец осаждающегося дихромата серебра вокруг кристалла нитрата серебра, помещенного в гель, содержащий дихромат калия. Химическая реакция, протекающая в ходе данного процесса, описывается уравнением:

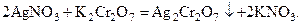
Первое обоснование возникновения периодических структур типа колец Лизеганга было дано В. Оствальдом в 1897 г. на основании развитых им представлений о пересыщении растворов [12]. Согласно представлениям Оствальда периодичность обусловлена переходом раствора из метастабильного состояния в лабильное, и наслоения служат доказательством существования метастабильных границ. Когда кон­центрация продукта реакции, образовавшегося за счёт взаимодействия реагентов (внутреннего, находящегося в растворе, и внешнего, поступающего в него), достигает метастабильной границы, начинается выпадение осадка. Образование наслоений обусловлено передвижением пересыщенного раствора, расположенного за метастабильной границей. Этот раствор как бы сносится током диффундирующего внешнего компонента. За метастабильной границей при встрече потока внешнего компонента с новыми порциями внутреннего компонента вновь начинается образование пересыщенного раствора продукта реакции, концентрация которого постепенно возрастает, пока вновь не достигнет метастабильной границы. И, таким образом, процесс повторяется.

Для реализации оствальдовской модели образования периодических структур необходимо, чтобы имели место достаточно высокие степени пересыщения, что возможно при кристаллизации малорастворимых веществ.