|
Главная |
Метод непосредственного интегрирования
|
из
5.00
|
Метод непосредственного интегрирования основан на преобразовании подинтегральной функции, применении свойств неопределённого интеграла и приведении подинтегрального выражения к табличной форме.
Например:
1) 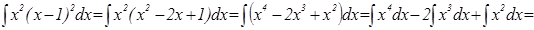
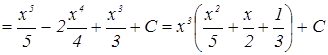
Проверка(на основании свойства №2 неопределённого интеграла):
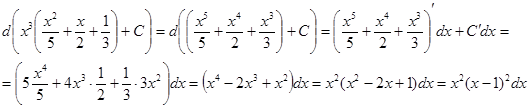
2) 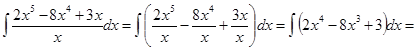
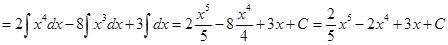
Проверка(на основании свойства №1 неопределённого интеграла): 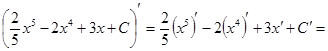
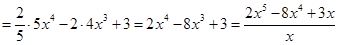
2. Метод подстановки (замены переменной)
Этот метод основан на введении новой переменной. В интеграле 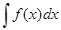 сделаем подстановку:
сделаем подстановку:
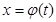 , тогда
, тогда
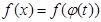 ;
;
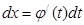 ;
;
Следовательно, получим:
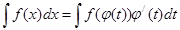
Например:
1) 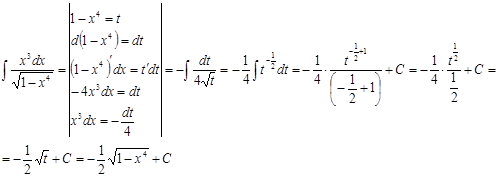
Проверка: 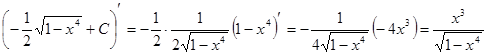
2) 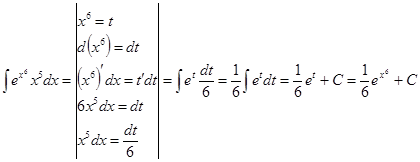
Проверка(на основании свойства №2 неопределённого интеграла):
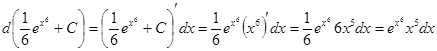
Интегрироване по частям
Пусть u иv - дифференцируемые функции. Раскроем дифференциал произведения этих функций:
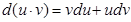 ,
,
откуда 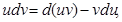
Проинтегрируем полученное выражение:
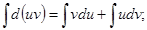
Тогда
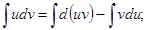
или
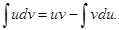
Например:
Проверка(на основании свойства №1 неопределённого интеграла):
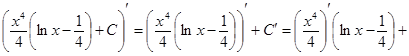
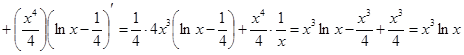
2) 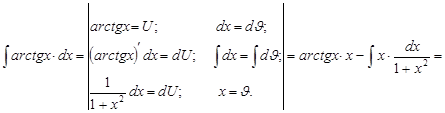
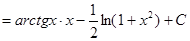
Решаем 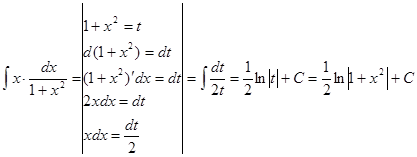
Проверка(на основании свойства №1 неопределённого интеграла):
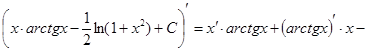
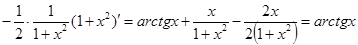
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задачи для домашнего решения
Найти интеграл:
I. Метод непосредственного интегрирования
а) 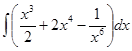 ; е)
; е) 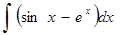 ;
;
б) 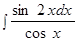 ; ж)
; ж) 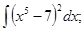
в) 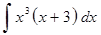 ; з)
; з) 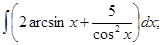
г) 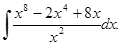 ; и)
; и) 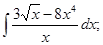
д) 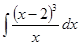 ; к)
; к) 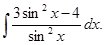
II. Метод подстановки (замены переменной)
а) 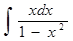 ; е)
; е) 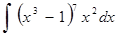 ;
;
б) 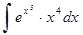 ; ж)
; ж) 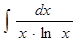 ;
;
в) 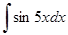 ; з)
; з) 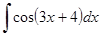 ;
;
г) 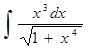 ; и)
; и) 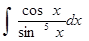 ;
;
д) 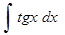 ; к)
; к) 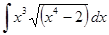 .
.
III. Метод интегрирования по частям
а) 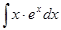 ; в)
; в) 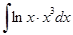 ; д)
; д) 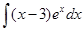
б) 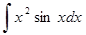 ; г)
; г) 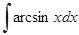 ; е)
; е) 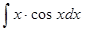
Задачи для решения на практических занятиях:
I. Метод непосредственного интегрирования
а) 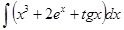 ; ж)
; ж)  ;
;
б) 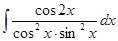 ; з)
; з) 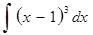 ;
;
в) 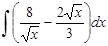 ; и)
; и) 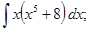
г) 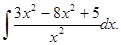 ; к)
; к) 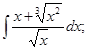
д) 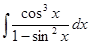 ; л)
; л) 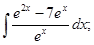
е)  ; м)
; м) 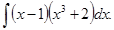
II. Метод подстановки (замены переменной)
а) 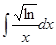 ; ж)
; ж) 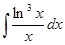 ;
;
б) 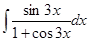 ; з)
; з) 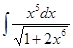 ;
;
в) 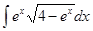 ; и)
; и) 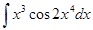 ;
;
г) 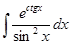 ; к)
; к) 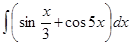 ;
;
д) 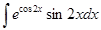 ; л)
; л) 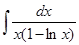 ;
;
е) 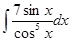 ; м)
; м) 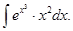
III. Метод интегрирования по частям
а) 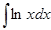 ; д)
; д) 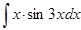 ;
;
б) 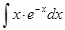 ; е)
; е) 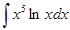 ;
;
в) 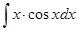 ; ж)
; ж) 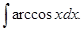
г) 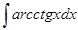 ;
;
ТЕМА №4
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
При математических расчётах часто требуется найти приращение первообразной функции при изменении её аргумента в заданных пределах. Такую задачу приходится решать при вычислении площадей и объёмов различных фигур, при определении среднего значения функции, при вычислении работы переменной силы. Эти задачи могут быть решены вычислением соответствующих определённых интегралов.
Цель занятия:
1. Научиться вычислять определённый интеграл с помощью формулы Ньютона-Лейбница.
2. Уметь применять понятие определённого интеграла для решения прикладных задач.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Рассмотрим задачу о нахождении площади криволинейной трапеции.
Пусть дана некоторая функция y=f(x), график которой изображён на рисунке.
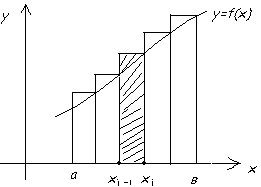
Рис 1. Геометрический смысл определенного интеграла.
На оси 0х выберем точки “a”и “в” и восстановим из них перпендикуляры до пересечения с кривой. Фигура ограниченная кривой, перпендикулярами и осью 0х называется криволинейной трапецией. Разобьём интервал 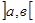 на ряд небольших отрезков. Выберем произвольный отрезок
на ряд небольших отрезков. Выберем произвольный отрезок 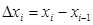 . Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:
. Достроим криволинейную трапецию, соответствующую этому отрезку до прямоугольника. Площадь такого прямоугольника определится как:
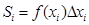 .
.
Тогда площадь всех достроенных прямоугольников в интервале 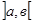 будет равна:
будет равна:
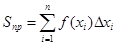 ;
;
Если каждый из отрезков достаточно мал и стремится к нулю, то суммарная площадь прямоугольников будет стремиться к площади криволинейной трапеции:
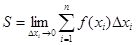 ;
;
Итак, задача о вычислении площади криволинейной трапеции сводится к определению предела суммы.
Интегральная сумма есть сумма произведений приращения аргумента на значение функции f(x), взятой в некоторой точке интервала, в границах которого изменяется аргумент. Математически задача о нахождении предела интегральной суммы, если приращение независимой переменной стремится к нулю, приводит к понятию определённого интеграла.
Функция f(x) в некотором интервале от х=адо х=в интегрируема, если существует такое число, к которому стремится интегральная сумма при Dх®0. В этом случае число J называют определённым интегралом функции f(x) в интервале 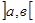 :
:
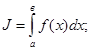
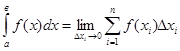 ;
;
где ]а, в[ – область интегрирования,
а–нижний предел интегрирования,
в–верхний предел интегрирования.
Таким образом, с точки зрения геометрии, определённый интеграл есть площадь фигуры, ограниченной графиком функции в определённом интервале ]а, в[ и осью абцисс.
|
из
5.00
|
Обсуждение в статье: Метод непосредственного интегрирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы