Теоретические положения. Определение параметров и квантилей распределения (расчетных климатических

Определение параметров и квантилей распределения (расчетных климатических характеристик) при наличии данных наблюдений достаточной продолжительности осуществляется путем применения аналитических функций распределения ежегодных вероятностей превышения - кривых обеспеченностей.

Эмпирическая ежегодная вероятность превышения P_m метеорологических характеристик определяется по формуле:

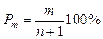, (36)

где m - порядковый номер членов ряда метеорологической характеристики, расположенного в убывающем порядке; n - общее число членов ряда.

Эмпирические кривые распределения ежегодных вероятностей превышения строятся на клетчатках вероятностей. Тип клетчатки вероятностей выбирается в соответствии с принятой аналитической функцией распределения вероятностей и полученного отношения коэффициента асимметрии C_s к коэффициенту вариации С_v.. Наиболее распространенной является клетчатка нормального закона распределения.

Для сглаживания и экстраполяции эмпирических кривых распределения ежегодных вероятностей превышения, как правило, применяются трехпараметрические распределения: Крицкого-Менкеля (гамма-распределение) при любом отношении С_s/С_v и распределение Пирсона III типа (биномиальная кривая) при С_s/С_v³ 2 и другие распределения, имеющие предел простирания случайной переменной от нуля, или положительного значения, до бесконечности. При надлежащем обосновании допускается применять двухпараметрические распределения, если эмпирическое отношение С_s/С_v и аналитическое отношение С_s/С_v, свойственное данной функции распределения, приблизительно равны. При неоднородности ряда наблюдений применяются усеченные и составные кривые распределения вероятностей превышения.

Оценки параметров аналитических кривых распределения: среднее многолетнее значение 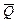, коэффициент вариации С_v и отношение коэффициента асимметрии к коэффициенту вариации C_s/C_v, устанавливаются по рядам наблюдений за рассматриваемой метеорологической характеристикой методом приближенно наибольшего правдоподобия, методом моментов, методом наименьших квадратов.

Коэффициент вариации С_v и коэффициент асимметрии С_s для трехпараметрического гамма-распределения следует определять методом приближенно наибольшего правдоподобия в зависимости от статистик 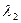и 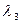, вычисляемых по формулам:

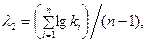( 37 )

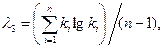( 38 )

где k - модульный коэффициент рассматриваемой метеорологической характеристики, определяемый по формуле:

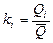, ( 39 )

Q_i - погодичные значения метеорологических характеристик; 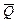- среднее арифметическое значение, определяемое в зависимости от числа лет наблюдений по формуле:

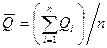. ( 40 )

По полученным значениям статистик l₂ и l₃ определяют коэффициенты вариации и асимметрии по специальным таблицам, номограммам или на основе вычислительной программы.

Коэффициенты вариации С_v и асимметрии С_s определяются методом моментов по формулам:

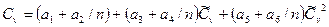, ( 41 )

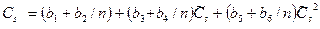( 42 )

где a₁ , ... a₆; b₁ ,... b₆ - коэффициенты, определяемые по специальным таблицам; 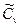и 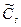- соответственно смещенные оценки коэффициентов вариации и асимметрии, определяемые по формулам:

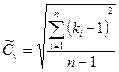, ( 43 )

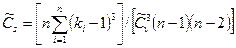( 44 )

При С_v <0,6 и С_s<1,0 допускается использовать формулы (43) и (44) без учета поправок на смещение.

Случайные средние квадратические погрешности выборочных средних определяются по приближенной зависимости:

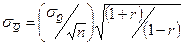, ( 45 )

которая применяется при коэффициенте автокорреляции между смежными членами ряда r меньшем 0.5. При больших коэффициентах автокорреляции используется формула:

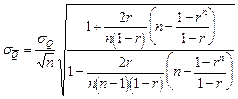
( 46 )

Случайные средние квадратические ошибки коэффициентов вариации при C_s = 2C_v определяются по зависимости:

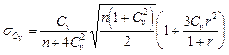( 47 )

В методе моментов среднее значение и коэффициент вариации определяется методом моментов, а отношение С_s/С_v – подбором при достижении минимума суммы квадратов отклонений между эмпирическим распределением и его аналитической аппроксимацией.

Нормированные ординаты распределения Пирсона III типа приведены в табл.17 Приложения, а относительные ординаты распределения Крицкого-Менкеля – в табл.18 Приложения.