 |
Главная |
Критерий Сэвиджа (критерий крайнего пессимизма)
|
из
5.00
|
Вопрос 1 Дискретная матричная модель воспроизводства населения.
Выразим количественные показатели межгрупповых переходов через соответствующие вероятности и численности выпускающих групп.



 –численность населения к-ого пола в 1-ой возрастной группе в момент времени
–численность населения к-ого пола в 1-ой возрастной группе в момент времени  ;
;
 – вероятность рождения ребёнка k-ого пола у женщины возраста
– вероятность рождения ребёнка k-ого пола у женщины возраста  ,
,  - начало и конец фертильного периода (возрастной интервал, когда женщина может иметь детей);
- начало и конец фертильного периода (возрастной интервал, когда женщина может иметь детей);
 –численность населения женского пола в
–численность населения женского пола в  -ой возрастной группе в момент времени
-ой возрастной группе в момент времени 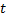 ;
;
 –численность населения мужского пола в
–численность населения мужского пола в  -ой возрастной группе в момент времени
-ой возрастной группе в момент времени 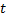 ;
;
 - сальдо миграции лиц -ого пола в 1-ой возрастной группе в момент времени
- сальдо миграции лиц -ого пола в 1-ой возрастной группе в момент времени  ;
;
 -вероятность дожития лиц -ого находящихся в
-вероятность дожития лиц -ого находящихся в  -ой возрастной группе до следующей возрастной группы (
-ой возрастной группе до следующей возрастной группы ( 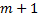 );
);  - последняя возрастная группа.
- последняя возрастная группа.
векторно-матричная форма записи.
Формируем вектор естественного состава населения. У него  компонент.
компонент.
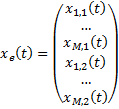
Формируем матрицу параметров естественного движения. Её размерность 


| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
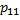
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| ||||||||

| 
| 
| 
| 
| 
| 
| ||||||||

| 
| 
| 
| 
| 
| 
| ||||||||

| 
| 
| 
| 
| 
| 
| ||||||||

| 
| 
| 
| 
| 
| 
| ||||||||

| 
| 
| 
| 
| 
| 
| ||||||||

| 
| 
| 
| 
| 
| 
| 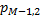
| 
|
Таким образом, дискретная матричная модель воспроизводства населения имеет вид:

Вопрос 2. Критерий выбора оптимальной стратегии в условиях полной неопределенности (игры с природой)
В экономических задачах часто выбор решения зависит от объективной действительности или окружающей экономической среды, которая в математических моделях называется «природой». Математические модели таких ситуаций называются «игры с природой».
игрок А - m стратегий. природа П - n состояний П1, …, Пn. Матрица игры:
| Ai\Пj | П1 | … | Пn |
| A1 | a11 | … | а1n |
| … | … | … | … |
| Am | a1m | … | amn |
Показателем благоприятности состояния Пj природы называется
 . (1)
. (1)
Для характеристики удачливости игрока А вводится понятие риска:
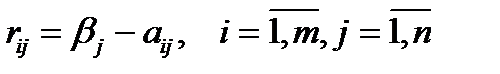 . (2)
. (2)
Таким образом, риск – это упущенная возможность получения максимального выигрыша  .
.
 . Для любой матрицы А можно составить матрицу рисков RA.
. Для любой матрицы А можно составить матрицу рисков RA.
Принятие решений в условиях полной неопределенности
Критерий Вальда (критерий крайнего пессимизма - максимин)
Показатель эффективности стратегии Ai - величина  , т.е. минимальный выигрыш. Выбираем максимум:
, т.е. минимальный выигрыш. Выбираем максимум:  .
.
Максимаксный критерий (критерий крайнего оптимизма)
Показатель эффективности стратегии Ai– это максимальный выигрыш по этой стратегии
 . Выбираем максимум.
. Выбираем максимум.
Критерий пессимизма-оптимизма Гурвица относительно выигрыша
Показатель эффективности стратегии  .
.
Оптимальной стратегией Ai0 считается стратегия с максимальным показателем эффективности
При λ = 0 получаем критерий Вальда, а если λ = 1 получаем максимаксный критерий.
Критерий Сэвиджа (критерий крайнего пессимизма)
Показатель неэффективности - максимальный риск  .
.
Оптимальной является стратегия Ai0 с минимальным показателем неэффективности.
|
из
5.00
|
Обсуждение в статье: Критерий Сэвиджа (критерий крайнего пессимизма) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

