Постановки задачи нелинейного программирования

Напомним сначала постановку задачи линейного программирования:

найти , такой что

на множестве допустимых решений, заданных ограничениями

, .

Задача нелинейного программирования формулируется аналогично:

найти вектор , (или точку ), такой (такую), что целевая функция достигает максимума (минимума):

(4.5)

на множестве допустимых решений, заданных ограничениями

, (4.6)

Задача сводится к нахождению условного экстремума функции 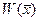при ограничениях, которые задаются неравенствами.

Принципиальным отличием является отсутствие требования линейности целевой функции и ограничений, и это отличие говорит о том, что решение не обязательно лежит на границе области допустимых решений, оно может оказаться внутренней точкой области.

Оставляя в стороне вопрос о существовании решения поставленной задачи, можно предложить следующий алгоритм решения:

- находим стационарные точки (подозрительные на экстремум) функции и сохраняем те из них, координаты которых удовлетворяют условиям (4.6);

- находим точки, в которых может достигаться экстремум функции Лагранжа:

- вычисляем значения целевой функции 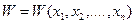во всех найденных точках и находим её глобальный максимум (или минимум).

Если функцию 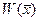интерпретировать как доход (стоимость), а 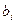— как объемы некоторых ресурсов, то множители Лагранжа показывают, как изменится максимальный доход (минимальная стоимость), если количество ресурса 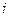-го вида увеличить на единицу.

Пример. Найти наибольшее и наименьшее значения целевой функции (т.е. её глобальные и ) целевой функции

(4.5*)

на множестве допустимых решений, заданных ограничением:

. (4.6*)

Решение.

1. Находим стационарные точки (точки, подозрительные на экстремум) функции и сохраняем те из них, координаты которых удовлетворяют условиям (4.6*).

Для этого решаем систему

, получаем ,

т.е. точку , удовлетворяющую условиям (4.6*) и являющуюся внутренней точкой области допустимых решений.

2. Находим точки, в которых может достигаться экстремум функции Лагранжа:

.

Для этого решаем систему:

,

получаем

, , ,

т.е. шесть точек, лежащих на границе области допустимых решений:

, , , ,

. .

3. Вычисляем значения целевой функции во всех найденных точках:

, ,

, .

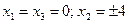Ответ: , достигается при , во внутренней точке области допустимых решений, , достигается при , на границе области допустимых решений.

К сожалению, такой прямой алгоритм решения иногда при практической реализации наталкивается на множество трудностей. Разработан ряд методов решения некоторых специальных задач нелинейного программирования.