 |
Главная |
Задачи для самостоятельного решения. 1. Пусть имеется три склада и четыре пункта потребления
|
из
5.00
|
1. Пусть имеется три склада и четыре пункта потребления.
Запасы товара на складах:  . Потребности пунктов потребления:
. Потребности пунктов потребления:  .
.
Стоимость перевозки единицы товара со склада  в пункт
в пункт  задана матрицей:
задана матрицей:
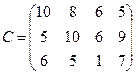 .
.
Составить наиболее экономичный план перевозок товара со складов в пункты потребления.
2. Напишите математическую постановку транспортной задачи, если матрица удельных транспортных затрат имеет вид: 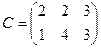 , вектор производства
, вектор производства  , вектор потребления
, вектор потребления 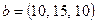 .
.
3. Найдите начальный опорный план транспортной задачи двумя методами, сравните значения целевой функции для полученных планов:
 .
.
Глава 3. Целочисленное программирование
Очень часто из содержательного смысла задачи линейного программирования вытекает необходимость нахождения решения только в целочисленной форме. Строго говоря, такие задачи не относятся к задачам линейного программирования в их изначальном понимании и классической постановке, поэтому их выделяют в отдельный класс целочисленного или дискретного программирования.
Рассмотрим несколько типов таких задач.
Задача о назначении
Имеется  работ и
работ и  кандидатов на эту работу. Назначению
кандидатов на эту работу. Назначению  ого кандидата
ого кандидата  на
на  ую работу
ую работу  соответствует число
соответствует число  — эффективность или затраты такого назначения. Каждого кандидата можно назначать только на одну работу, на каждую работу должен быть подобран один кандидат. Распределение кандидатов по работам должно обеспечить максимум эффективности или минимум затрат.
— эффективность или затраты такого назначения. Каждого кандидата можно назначать только на одну работу, на каждую работу должен быть подобран один кандидат. Распределение кандидатов по работам должно обеспечить максимум эффективности или минимум затрат.
Математическая модель задачи о назначении.
Найти максимум (минимум) целевой функции  , где
, где  — элементы матрицы эффективности (затрат):
— элементы матрицы эффективности (затрат):
 .
.
при заданных ограничениях:


где 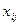 — искомые переменные, могут принимать значения только 0 или 1:
— искомые переменные, могут принимать значения только 0 или 1:

| если  й кандидат назначается на й кандидат назначается на  ю работу,
в противном случае. ю работу,
в противном случае.
|
В такой постановке задачу можно решать путем простого перебора возможных значений искомых переменных. Число вариантов при этом будет равно  . Очевидно, что при больших значениях
. Очевидно, что при больших значениях  прямой перебор становится нерациональным или даже практически невозможным.
прямой перебор становится нерациональным или даже практически невозможным.
Наиболее распространен венгерский метод решения задачи. Основой метода является следующая теорема.
Пусть матрица  получена из матрицы
получена из матрицы  уменьшением (увеличением) элементов строки (столбца) на одно и то же число
уменьшением (увеличением) элементов строки (столбца) на одно и то же число  . Тогда максимум или минимум целевой функции
. Тогда максимум или минимум целевой функции  достигается на том же наборе переменных
достигается на том же наборе переменных  .
.
Предположим, мы ищем максимум (минимум) целевой функции и нам удалось за несколько шагов, уменьшая или увеличивая на каждом шаге элементы строки или столбца очередной матрицы, получить матрицу  , где
, где 
 , причем в любой строке и в любом столбце обязательно находится хотя бы один ноль. Тогда
, причем в любой строке и в любом столбце обязательно находится хотя бы один ноль. Тогда
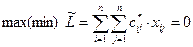
достигается выбором  нулей, стоящих в разных строках и разных столбцах матрицы
нулей, стоящих в разных строках и разных столбцах матрицы  . Положение каждого нуля определяется индексом
. Положение каждого нуля определяется индексом  , причём
, причём  при
при  ,
,  при
при  , т.е. составляющие индекса, стоящие на одних и тех же местах, не повторяются. Положение выбранных нулей определяет выбор искомых переменных:
, т.е. составляющие индекса, стоящие на одних и тех же местах, не повторяются. Положение выбранных нулей определяет выбор искомых переменных:
 , когда индекс
, когда индекс 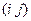 совпадает с индексом
совпадает с индексом  ;
;
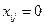 во всех остальных случаях.
во всех остальных случаях.
Условия  ,
,  , в силу не повторения составляющих индексов
, в силу не повторения составляющих индексов  , выполнены.
, выполнены.
Для задачи в первоначальной постановке с исходной матрицей  максимум (минимум) целевой функции
максимум (минимум) целевой функции 
 достигается на том же наборе переменных
достигается на том же наборе переменных  .
.
Алгоритм решения задачи о назначении, то есть поиск  , венгерским методом имеет несколько шагов.
, венгерским методом имеет несколько шагов.
Шаг 1. Дана матрица эффективности (затрат):
 .
.
1.1. В каждой строке матрицы  находят наибольший (наименьший) элемент
находят наибольший (наименьший) элемент  , который вычитают из всех элементов данной строки. Получают матрицу
, который вычитают из всех элементов данной строки. Получают матрицу  .
.
1.2. В каждом столбце матрицы  находят наибольший (наименьший) элемент
находят наибольший (наименьший) элемент  , который вычитают из всех элементов данного столбца. Получают матрицу
, который вычитают из всех элементов данного столбца. Получают матрицу  .
.
Шаг 2.
2.1. Рассматривается одна из строк матрицы  , имеющая наименьшее число нулей, отмечают знаком «*» один из нулей этой строки и зачёркивают все остальные нули этой строки и того столбца, в котором стоит отмеченный знаком «*» нуль — 0*.
, имеющая наименьшее число нулей, отмечают знаком «*» один из нулей этой строки и зачёркивают все остальные нули этой строки и того столбца, в котором стоит отмеченный знаком «*» нуль — 0*.
2.2. Аналогичная операция выполняется для всех строк, при выполнении каждой следующей операции уже зачёркнутые нули игнорируются.
2.3. Если после выполнения операций в каждой строке и каждом столбце стоит отмеченный знаком «*» нуль, то оптимальное решение найдено. В противном случае переходят к шагу 3.
Шаг 3.
3.1. В матрице  отмечают знаком «^».
отмечают знаком «^».
3.1.1. все строки, в которых нет ни одного нуля 0*;
3.1.2. все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных знаком «^» строчек;
3.1.3. все строки, содержащие отмеченные нули 0* хотя бы в одном из отмеченных «^» столбцов.
3.2. Шаги 3.1.2. и 3.1.3. повторяют до тех пор, пока есть что отмечать.
3.3. Зачёркивают все неотмеченные строки и каждый отмеченный столбец в матрице  . В остатке после зачёркивания нет ни одного нулевого элемента. Запоминают
. В остатке после зачёркивания нет ни одного нулевого элемента. Запоминают  наибольший (наименьший) из них.
наибольший (наименьший) из них.
Шаг 4.
4.1. Вычитают  из всех элементов, не вычеркнутых столбцов матрицы
из всех элементов, не вычеркнутых столбцов матрицы  . Получают матрицу
. Получают матрицу 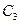 .
.
4.2. Прибавляют  ко всем элементам строк матрицы
ко всем элементам строк матрицы 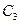 , которые соответствуют строкам, вычеркнутым в
, которые соответствуют строкам, вычеркнутым в  . Получают матрицу
. Получают матрицу  .
.
Если в каждой строке и каждом столбце матрицы  стоит нуль (отмеченный 0* или неотмеченный, перечёркнутый или нет), то оптимальное решение найдено. Иначе цикл повторяют, начиная с шага 2.
стоит нуль (отмеченный 0* или неотмеченный, перечёркнутый или нет), то оптимальное решение найдено. Иначе цикл повторяют, начиная с шага 2.
Пример 1.
Пусть для монтажа четырёх объектов требуется четыре крана. Известна матрица затрат  , где
, где  — время монтажа
— время монтажа  ым краном
ым краном 
 ого объекта
ого объекта  :
:
 .
.
Распределить краны по объектам так, чтобы суммарное время монтажа было минимальным.
Математическая постановка задачи:
Найти 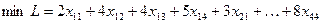
при условиях:

. . .
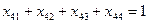

. . .

для 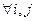
 или
или 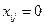 .
.
Заметим, что исходная матрица является матрицей затрат.
Шаг 1. Модифицируем исходную матрицу затрат.
1.1. В каждой строке матрицы  найдем наименьший элемент и вычтем его из всех элементов данной строки. От элементов первой строки отнимем число 2. От элементов первой строки отнимем число 3. От элементов первой строки отнимем число 2. От элементов первой строки отнимем число 3. Получим матрицу
найдем наименьший элемент и вычтем его из всех элементов данной строки. От элементов первой строки отнимем число 2. От элементов первой строки отнимем число 3. От элементов первой строки отнимем число 2. От элементов первой строки отнимем число 3. Получим матрицу  .
.
1.2. В каждом столбце матрицы  найдем наименьший элемент и вычтем его из всех элементов данного столбца. От элементов второго столбца отнимем число 2, от элементов четвёртого столбца отнимем число 3. Получим матрицу
найдем наименьший элемент и вычтем его из всех элементов данного столбца. От элементов второго столбца отнимем число 2, от элементов четвёртого столбца отнимем число 3. Получим матрицу  .
.
 Þ
Þ  .
.
Шаг 2.
2.1. Выбираем вторую строку матрицы  , в ней всего один нуль, отмечаем его знаком «*». Так как отмеченный нуль находится в первом столбце, зачеркиваем все остальные нули в этом столбце. Для зачеркнутых нулей будем использовать символ Æ.
, в ней всего один нуль, отмечаем его знаком «*». Так как отмеченный нуль находится в первом столбце, зачеркиваем все остальные нули в этом столбце. Для зачеркнутых нулей будем использовать символ Æ.

2.2. Аналогичную операцию выполним сначала для третьей строки, затем для первой. Получим:
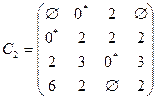 .
.
Если после выполнения в каждой строке и каждом столбце стоит отмеченный нуль, то оптимальное решение найдено. В нашем примере это условие не выполнено, потому перейдем к шагу 3.
Шаг 3.
3.1.1. Отметим четвертую строку знаком «^», так как в ней нет ни одного отмеченного нуля 0*.
3.1.2. Отметим третий столбец, содержащий перечеркнутый нуль в четвертой отмеченной знаком «^» строчке.
3.1.3. Отметим третью строку, содержащую 0* в третьем, отмеченном знаком «^» столбце.
Больше вычеркивать нечего, получаем матрицу  с помеченными строками и столбцами.
с помеченными строками и столбцами.



3.2. Вычеркнем все неотмеченные строки и каждый отмеченный столбец в матрице  , остаток после зачёркивания строк (1), (2). и столбца (3) имеет вид:
, остаток после зачёркивания строк (1), (2). и столбца (3) имеет вид:
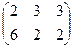 ,
,
наименьший из элементов полученной матрицы 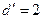 .
.
Шаг 4.
4.1. Вычтем значение 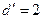 из всех элементов, не вычеркнутых столбцов матрицы
из всех элементов, не вычеркнутых столбцов матрицы  . Это будут элементы всех столбцов, за исключением третьего. Получим матрицу
. Это будут элементы всех столбцов, за исключением третьего. Получим матрицу 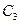 .
.
4.2. Прибавим  ко всем элементам строк матрицы
ко всем элементам строк матрицы 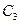 , которые соответствуют строкам, вычеркнутым в
, которые соответствуют строкам, вычеркнутым в  . Получим матрицу
. Получим матрицу  .
.
 Þ
Þ  .
.
В матрице  в каждой строке и каждом столбце имеется хотя бы один ноль. Их расположение показывает, что оптимальное решение достигается на наборе
в каждой строке и каждом столбце имеется хотя бы один ноль. Их расположение показывает, что оптимальное решение достигается на наборе  . Все остальные
. Все остальные 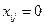 .
.
Ответ:  , т.е первый кран направляется на монтаж второго объекта, второй кран — на монтаж первого, третий кран монтирует третий объект, и четвертый кран — объект с номером четыре.
, т.е первый кран направляется на монтаж второго объекта, второй кран — на монтаж первого, третий кран монтирует третий объект, и четвертый кран — объект с номером четыре.
Задача коммивояжера
Имеется  городов, занумерованных числами от 1 до
городов, занумерованных числами от 1 до  . Коммивояжер, выезжая из города 1, должен побывать в каждом городе ровно один раз и вернуться в исходный пункт. Известны расстояния между городами:
. Коммивояжер, выезжая из города 1, должен побывать в каждом городе ровно один раз и вернуться в исходный пункт. Известны расстояния между городами:  , где
, где  .
.
Требуется найти самый короткий (дешевый) маршрут.
Математическая модель имеет вид:
Найти минимум целевой функции 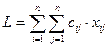 ,
,
где  — элементы матрицы расстояний (стоимостей переходов между городами):
— элементы матрицы расстояний (стоимостей переходов между городами):
 ,
,
при заданных ограничениях:
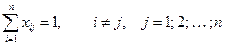 (1)
(1)
 (2)
(2)
где 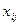 — искомые переменные, могут принимать значения только 0 или 1:
— искомые переменные, могут принимать значения только 0 или 1:

| если в маршрут входит переезд из 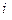 в в  ;
в противном случае. ;
в противном случае.
| (3) |
Ограничения (1)  (3) отражают требования однократного въезда и выезда из каждого города, но полностью не описывают допустимые маршруты.
(3) отражают требования однократного въезда и выезда из каждого города, но полностью не описывают допустимые маршруты.
Диагональные элементы матрицы 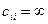 , что означает запрет на переход
, что означает запрет на переход 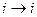 . При численной реализации их полагают равными достаточно большому числу.
. При численной реализации их полагают равными достаточно большому числу.
Заметим, что в общем случае  , хотя обычно решают задачи с симметричной матрицей
, хотя обычно решают задачи с симметричной матрицей  .
.
На практике для решения задачи коммивояжера используется метод ветвей и границ, обладающий эффективным алгоритмом. Этот метод можно использовать для решения вручную задач небольшой размерности.
Реализация метода ветвей и границ в применении к задачи коммивояжера включает два основных момента: использование приведенных матриц и алгоритм разбиения маршрута на подмаршруты.
Для задачи коммивояжера, так же как для транспортной задачи и задачи о назначениях, операция преобразования исходной матрицы  , заключающаяся в прибавлении или отнимании постоянных величин
, заключающаяся в прибавлении или отнимании постоянных величин  , по строкам и
, по строкам и  по столбцам не меняет экстремальных свойств задачи,
по столбцам не меняет экстремальных свойств задачи,  .
.
Такая операция называется приведением матрицы, константы
 и
и  называют приводящими константами, а полученная в результате матрица — приведенной матрицей.
называют приводящими константами, а полученная в результате матрица — приведенной матрицей.
Рассмотрим решение задачи на конкретном примере.
Пример 1. Решите задачу о коммивояжере с матрицей стоимости переходов:
 .
.
Метод является итерационным, на каждом шаге производится ветвление маршрута, обеспечивающее оптимальную стратегию.
Итерация 0. Вычисление начальной оценки маршрута.
Операция приведения. Для вычисления нижней границы величины затрат на любой допустимый маршрут для заданной матрицы  используется операция приведения.
используется операция приведения.
Для удобства запишем матрицу  в виде таблицы, с указанием номеров строк и столбцов. Найдем приведенные константы
в виде таблицы, с указанием номеров строк и столбцов. Найдем приведенные константы  по строкам, они равны минимальному элементу в соответствующей строке.
по строкам, они равны минимальному элементу в соответствующей строке.

| |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ | |||||||
| ¥ |
Вычтем эти константы из элементов соответствующих строк:
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
Теперь найдем приведенные константы  по столбцам:
по столбцам:
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||

|
Вычтем константы из элементов соответствующих столбцов, получим «приведенную» таблицу 3.1., обозначим ее  :
:
Таблица 3.1. Приведенная таблица 
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
Оценка маршрута. Рассчитаем  — нижнюю границу величины затрат на любой допустимый маршрут:
— нижнюю границу величины затрат на любой допустимый маршрут:
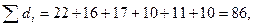

 .
.
Далее решение состоит из последовательности итераций, на каждой из которых выбирается очередной переход из одного города в другой.
Итерация 1.Ветвление маршрута. Выбор первого перехода.
Оценка переходов. На входе имеем приведенную матрицу  . Множество возможных маршрутов
. Множество возможных маршрутов  , соответствующих текущей приведенной матрице, делится на два подмаршрута
, соответствующих текущей приведенной матрице, делится на два подмаршрута  относительно некоторого выбранного перехода из города
относительно некоторого выбранного перехода из города 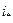 в город
в город  , обозначим его
, обозначим его  . В маршрут
. В маршрут  обязательно входит выбранный переход
обязательно входит выбранный переход  , в маршрут
, в маршрут  этот переход не входит.
этот переход не входит.
На нулевой итерации в качестве перехода можно взять любой из переходов, для которого соответствующий элемент приведенной матрицы  , то есть «приведенная» стоимость перехода равна нулю.
, то есть «приведенная» стоимость перехода равна нулю.
Рассмотрим эти переходы, построенные на основе приведенной таблицы 3.1. и проведем их оценку. Для каждого такого перехода  оценка вычисляется
оценка вычисляется  , где
, где  равен наименьшему из элементов в строке
равен наименьшему из элементов в строке 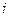 , не считая элемента на позиции
, не считая элемента на позиции  , а
, а  равен наименьшему из элементов в столбце
равен наименьшему из элементов в столбце  , не считая элемента на позиции
, не считая элемента на позиции  .
.
Например,  ,
,  ,
, 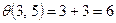 ,
,  и так далее. Результаты расчетов приведены в таб. 3.2.
и так далее. Результаты расчетов приведены в таб. 3.2.
Таблица 3.2. Оценки переходов для матрицы 
| |||||||
| Переходы | (1;6) | (2;4) | (3;5) | (4;3) | (5;3) | (6;1) | (6;2) |
| Оценки |
Максимальная из оценок получена для перехода  , который будет являться точкой ветвления маршрута. Эта точка делит все множество маршрутов на два подмножества
, который будет являться точкой ветвления маршрута. Эта точка делит все множество маршрутов на два подмножества  , маршрут
, маршрут  включает переход
включает переход  , а
, а  не включает, такой переход назовем «запрещенным» для маршрута
не включает, такой переход назовем «запрещенным» для маршрута  .
.
Оценка маршрутов. Следующий шаг — необходимо оценить маршруты  ,
,  и выбрать из них с меньшей оценкой.
и выбрать из них с меньшей оценкой.
Прежде всего, заметим, что фиксируя некоторый переход  для маршрута, нужно не допустить образования цепочек переходов, которые приводят к зацикливанию, то есть прохождению некоторых городов несколько раз. Поэтому нужно обязательно запретить обратный переход
для маршрута, нужно не допустить образования цепочек переходов, которые приводят к зацикливанию, то есть прохождению некоторых городов несколько раз. Поэтому нужно обязательно запретить обратный переход  . Кроме этого могут возникать и другие «запрещенные» маршруты.
. Кроме этого могут возникать и другие «запрещенные» маршруты.
Оценка  . Маршрут включает переход
. Маршрут включает переход  , значит, переход
, значит, переход 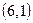 должен быть запрещен. Других запрещенных переходов нет. Такому маршруту будет соответствовать матрица
должен быть запрещен. Других запрещенных переходов нет. Такому маршруту будет соответствовать матрица  , полученная из
, полученная из  путем :
путем :
1) вычеркивания элемента  , то есть 1-ой строки и 6-ого столбца;
, то есть 1-ой строки и 6-ого столбца;
2) запрета перехода 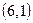 , для этого элемент полагают равным бесконечно большому числу
, для этого элемент полагают равным бесконечно большому числу  :
:
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
Оценка маршрута, который описывается полученной матрицей, осуществляется по уже известному алгоритму, используя операцию приведения. Эта матрица уже имеет нули во всех строках, значит:

нули есть и во всех столбцах, кроме первого, в котором минимальный элемент равен 1, следовательно:

Полная оценка подмаршрута  :
:
 .
.
Приведенная матрица  приведена в таблице 3.3.
приведена в таблице 3.3.
Таблица 3.3. Приведенная матрица 
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
Оценка  . Подмаршрут не включает переход
. Подмаршрут не включает переход  , значит, его нужно запретить. Такому подмаршруту будет соответствовать матрица
, значит, его нужно запретить. Такому подмаршруту будет соответствовать матрица  , в которой:
, в которой:
1) элемент 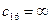 , что и означает запрет перехода
, что и означает запрет перехода  .
.
| ¥ | ¥ | |||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ | ||||||
| ¥ |
Оценка маршрута, который описывается полученной матрицей, осуществляется по уже известному алгоритму, используя операцию приведения. Эта матрица уже имеет нули во всех строках, кроме первой, минимальный элемент которой равен 13, значит, сумма приведенных констант по строкам равна:

нули есть и во всех столбцах, кроме последнего, в котором минимальный элемент равен 7, следовательно, сумма приведенных констант по столбцам равна:

Полная оценка подмаршрута  :
:
 .
.
Выбор подмаршрута.
Сравним оценки. Выбираем маршрут с меньшей оценкой, это будет  , так как
, так как  <
< 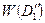 (
(  ).
).
Итерация 2.Выбор второго перехода.
Получен первый переход  , выберем второй.
, выберем второй.
Исходная матрица для расчетов получена на итерации 1, приведенная матрица  :
:
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ |
Повторим все шаги, проделанные на итерации 1.
Оценка переходов.
Не будем здесь останавливаться на подробных расчетах, приведем только таблицу оценок переходов для матрицы  .
.
Таблица 3.4. Оценки переходов для матрицы 
| |||||||
| Переходы | (2;1) | (2;4) | (3;5) | (4;1) | (4;3) | (53) | (6;2) |
| Оценки |
Максимальная из оценок получена для перехода  , который будет являться точкой ветвления маршрута. Эта точка делит все множество маршрутов на два подмаршрута
, который будет являться точкой ветвления маршрута. Эта точка делит все множество маршрутов на два подмаршрута  , маршрут
, маршрут 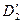 включает переход
включает переход  , а
, а  не включает.
не включает.
Оценка 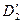 . Подмаршрут включает переход
. Подмаршрут включает переход  . Таким образом, с учетом первой итерации имеем
. Таким образом, с учетом первой итерации имеем  . Укажем переходы, которые нужно запретить для предотвращения зацикливания. Во-первых, так как мы включили в маршрут
. Укажем переходы, которые нужно запретить для предотвращения зацикливания. Во-первых, так как мы включили в маршрут  , переход
, переход  нужно запретить, в данном случае это уже учтено, так как на первой итерации 6-столбец уже был исключен. Во-вторых, нужно запретить также переход
нужно запретить, в данном случае это уже учтено, так как на первой итерации 6-столбец уже был исключен. Во-вторых, нужно запретить также переход  .
.
Таким образом, подмаршруту будет соответствовать матрица  , в которой:
, в которой:
1) вычеркнут элемент  , т.е. 6-я строка и 2-ой столбец;
, т.е. 6-я строка и 2-ой столбец;
2) элемент  , что означает запрет перехода
, что означает запрет перехода  .
.
| ¥ | ||||
| ¥ | ||||
| ¥ | ||||
| ¥ |
После этого полученная матрица, обозначим ее  , содержит нуль в каждой строке и каждом столбце, следовательно, оценка в целом подмаршрута
, содержит нуль в каждой строке и каждом столбце, следовательно, оценка в целом подмаршрута 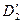 совпадает с оценкой маршрута на предыдущей итерации.
совпадает с оценкой маршрута на предыдущей итерации.

Оценка 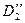 . Подмаршрут не включает переход
. Подмаршрут не включает переход  .
.
Таким образом, подмаршруту 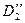 будет соответствовать матрица
будет соответствовать матрица  , в которой:
, в которой:
1) элемент 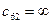 , что означает запрет перехода
, что означает запрет перехода  .
.
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | |||||
| ¥ | ¥ |
Эта матрица уже имеет нули во всех строках, кроме 6-ой, минимальный элемент которой равен 8. Значит, сумма приведенных констант по строкам равна:
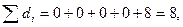
нули есть и во всех столбцах, кроме 2-го, в котором минимальный элемент равен 17, следовательно, сумма приведенных констант по столбцам равна:

Полная оценка подмаршрута 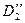 :
:
 .
.
Выбор подмаршрута.
Сравним оценки. Выбираем маршрут с меньшей оценкой, это будет 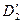 , так как
, так как 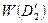 <
<  (
(  ).
).
Итерация 3.Выбор третьего перехода.
Получен маршрут  ,
,  , в котором исключены переходы
, в котором исключены переходы 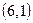 ,
,  ,
,  .
.
Найдем третий переход. Исходная матрица для расчетов получена на итерации 2, это — приведенная матрица  .
.
Повторим все шаги, проделанные на итерации 1.
| ¥ | ||||
| ¥ | ||||
| ¥ | ||||
| ¥ |
Оценка переходов.
Приведем таблицу оценок переходов для матрицы  .
.
Таблица 3.5. Оценки переходов для матрицы 
| Переходы | (2;4) | (3;5) | (4;1) | (4;3) | (53) |
| Оценки |
Максимальная из оценок получена для перехода  , который
, который
|
из
5.00
|
Обсуждение в статье: Задачи для самостоятельного решения. 1. Пусть имеется три склада и четыре пункта потребления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

