Метод потенциалов для сбалансированной задачи

Найденный начальный план затем улучшается методом потенциалов.

Рассмотрим алгоритм этого метода на конкретной задаче.

Пусть имеется три склада и четыре пункта потребления. Запасы товара на складах: . Потребности пунктов потребления: . Условия баланса выполнены.

Стоимости перевозок единицы товара со склада в пункт заданы матрицей:

.

Математическая постановка задачи.

(2.9)

Нахождение начального допустимого плана.Построим транспортную таблицу и составим допустимый начальный план методом северо-западного угла.

;

— — — — — —

 

Выделенная часть таблицы размерностью содержит значения допустимого плана, в левом верхнем углу каждой клетки указаны значения .

Клетки , , , , , назовем заполненными. Для всех остальных клеток , назовём их пустыми.

Искомые переменные, соответствующие заполненным клеткам, в нашем примере , , , , , , называют базисными переменными, а соответствующие не заполненным клеткам , , , , , — свободными.

Найденный начальный план необходимо также проверить на вырожденность. Вычислим , количество ненулевых переменных в полученном плане тоже равно 6. Полученный базисный план является невырожденным. Вычислим значение целевой функции:

Нахождение оптимального решения методом потенциалов.После определения начального базисного плана применяется метод потенциалов для нахождения оптимального решения.

Этот метод является итерационным, то есть решение состоит из последовательности шагов, на каждом из которых находится решение, улучшающее целевую функцию, пока не будет получено оптимальное решение.

Метод основан на введении некоторых неизвестных переменных, называемых потенциалами. Число таких потенциалов определяется размерностью задачи и равно .

Система потенциалов для полученного плана строится следующим образом: каждому складу ( ому пункту отправления) ставится в соответствие потенциал (число, определённое с точностью до постоянного слагаемого), а каждому ( ому пункту назначения) придается потенциал .

Каждая итерация состоит из следующих шагов:

Шаг 1. Построение системы потенциалов для текущего плана.

Шаг 2. Проверка текущего плана на оптимальность.

Шаг 3. Если текущий план не является оптимальным, с помощью условия оптимальности среди текущего множества свободных переменных выбирается переменная, которая становится базисной, а с помощью условия допустимости среди текущего множества базисных переменных определяется переменная, которая становится свободной.

Шаг 4. Если текущий план является оптимальным, решение заканчивается. Вычисляется оптимальное значение целевой функции.

Итерация 0.

Шаг 1.Построение системы потенциалов для текущего плана.

Неизвестные потенциалы , находятся из системы линейных алгебраических уравнений, составленной для базисных переменных текущего плана, то есть для заполненных клеток:

. (2.10)

Число базисных переменных для невырожденного плана равно , то есть на 1 меньше числа потенциалов. Поэтому один из потенциалов может принимать произвольное значение. Обычно полагают .

Таким образом, для рассматриваемой задачи имеем:

Базисные переменные (заполненные клетки)	Уравнения относительно потенциалов

Соответствующая система уравнений:

Так как , из второго и третьего уравнения находим, соответственно, , 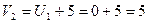. Зная , из четвертого уравнения найдем , и так далее , , .

Результаты расчетов приведены в таб. 2.1. Значение целевой функции для текущего плана было вычислено ранее 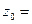2690.

Таблица 2.1. Итерация 0.
Пункты производства	Пункты назначения	Запасы
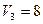
Потребности

 

Шаг 2. Проверяем текущий план на оптимальность. План считается оптимальным, если для всех незаполненных клеток таблицы 2.1 выполняется условие оптимальности:

или . (2.11)

Осуществляем проверку:

Свободные перемен- ные	Условие оптимальности	Выполнено да/нет
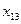
		нет
		нет
		да
		нет
		да
		да

Шаг 3.Условие оптимальности для текущего плана не выполнено. Надо улучшать план.

Шаг 3.1. Выбор новой базисной переменной.

Для улучшения плана необходимо переместить перевозку в свободную клетку, где условие оптимальности нарушено в большей степени, т.е. разность максимальна.

Соответствующая свободная переменная станет базисной.

В нашем случае это переменная , так как:

.

Шаг 3.2.Исключение текущей базисной переменной.

Среди текущего множества базисных переменных определяется переменная, которая становится свободной. Для этого необходимо сначала провести замкнутую ломаную линию, которая начинается и заканчивается в клетке, соответствующей вводимой переменной, в нашем примере . Пометим ее знаком «+».

Построенная замкнутая ломаная должна состоять только из горизонтальных и вертикальных линий, все вершины ломаной, кроме начальной, должны находиться в занятых клетках. Такую ломаную называют замкнутым циклом (рис. 2.4).

	5 – 20		2 +
	+ 210	– 40
		+ 120	– 60

Рис. 2.4. Замкнутый цикл

Далее каждой заполненной клетке, являющейся вершиной полученной ломаной, присваиваем последовательно знаки «–» или «+». Проведём ломаную . Найдем переменную, которую нужно исключить. Воспользуемся условием допустимости — среди клеток, помеченных знаком «–», выбирается клетка с наименьшим объемом перевозок. В нашем примере это клетка, соответствующая переменной , так как , .

Теперь для клеток со знаком « » уменьшаем объем перевозок на величину 20, а для клеток со знаком « »увеличиваем объем перевозок на величину 20 .

Таким образом, переменная стала свободной, а переменная стала базисной. Получен новый базисный план (рис. 2.5), жирным шрифтом указаны новые объемы перевозок.

150
	230

Рис. 2.5. Новый базисный план

Вычислим значение целевой функции:

2590< 2690. Значение целевой функции уменьшилось на 100 единиц. Для проверки оптимальности необходимо перейти к следующей итерации.

Итерация 1.

Выполняются последовательно шаги 1-2. На шаге 3 проверяется условие оптимальности текущего базисного плана (рис. 2.5). Результаты расчетов приведены в таб. 2.2, в ней указаны новые значения потенциалов. Значение целевой функции было вычислено выше 2590.

Условие оптимальности для текущего базисного плана не выполнено, так как получаем для не заполненных ячеек . Необходимо выполнить шаги 3.1 и 3.2, найти новый базисный план и перейти к следующей итерации.

Для трех переменных нарушено условие оптимальности, причем получено одно и то же положительное значение. Выберем новую базисную переменную , так ей соответствует меньшая стоимость перевозок.

Построим замкнутый цикл (таб. 2.2). Напомним, что повороты ломаной можно осуществлять только в занятых клетках. Так как , переменная становится свободной.

Таблица 2.2. Итерация 1.
Пункты производства	Пункты назначения	Запасы
		–			+
				+
		+			–
Потребности

 

Новый базисный план приведен на рис. 2.6, жирным шрифтом указаны новые объемы перевозок.

110
	230

Рис. 2.6. Новый базисный план

Значение целевой функции, полученное для нового базисного плана равно

.

Итерация 2.Повторим уже описанные действия шагов 1-3. Результаты расчетов потенциалов приведены в таб. 2.3.

Таблица 2.3. Итерация 2.
Пункты производства	Пункты назначения	Запасы
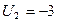
Потребности

Полученный план удовлетворяет условиям оптимальности:

Свободные перемен- ные	Условие оптимальности	Выполнено да/нет
		да
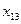
		да
		да
		да
		да
		да

 

При выполнении условия оптимальности принимаем имеющийся план, считая поставленную задачу решённой.

Ответ:

, .

Оптимальный план .

Заметим, что полученное решение не является единственным. Например, план , тоже является оптимальным с тем же значением целевой функции .

Подведём итог. Алгоритм решения транспортной задачи состоит из следующих шагов:

1. Определение начального плана одним из методов. Проверка плана на не вырожденность.

2. Построение системы потенциалов для имеющегося плана и ее решение.

3. Проверка плана на оптимальность и в случае его оптимальности принятие текущего плана, в случае не оптимальности осуществить переход к пункту 4.

4. Построение нового базисного плана, который становится текущим, затем переход к пункту 2.

Заметим, что иногда замкнутый цикл может само пересекаться. Рассмотрим ТЗ, заданную в матричном виде:

Найдем начальный допустимый план методом минимальной стоимости. Последовательность заполнения клеток , , , , .

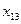План является невырожденным, количество заполненных клеток равно значению выражения . Можно решать методом потенциалов:

Найдем решение полученной системы:

, .

Вычислим для не заполненных ячеек 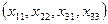соответственно.

Замкнутый цикл начинается и заканчивается в клетке :

6 5 1   +

Далее задачу решать методом потенциалов.

2.5. Вырожденный план

При решении ТЗ методом потенциалов на некоторых итерациях текущий план может оказаться вырожденным.

Рассмотрим сбалансированную транспортную задачу:

Найдем начальный допустимый план методом северо-западного угла.

Количество ненулевых компонент в начальном допустимом плане равно 6, что меньше чем . Такой план является вырожденным планом. В этом случае необходимо ввести в базисный план нулевые переменные и считать их базисными.

Заметим, что «потеря» базисной клетки происходит при заполнении клетки . Пункт производства исчерпан, и потребности пункта потребления выполняются полностью одновременно. В данном случае необходимо к базисным клеткам добавить клетку с нулевым значением, расположенную рядом с только что заполненной, которая обусловила потерю. Для нашей задачи базисной можно считать клетку или . Иногда в эту клетку помещают бесконечно малое число e.

.

Рассмотрим транспортную таблицу. Теперь план является невырожденным, количество заполненных клеток равно 7:

– – – – – – – –

Построим систему потенциалов и найдем решение системы:

, , .

Вычислим для соответствующих не заполненных ячеек . Теперь можно построить замкнутый цикл и решать далее задачу методом потенциалов. При нахождении очередного текущего плана не забывать проверять его на не вырожденность. Как с ней бороться мы уже знаем.