Первое действие второго и последующих шагов

Перепишем матрицу и вектор в соответствии с новыми наборами базисных и свободных переменных. (при этом на втором шаге осуществляется переход от (2) к (3), на следующих шага меняется (3)).

Перейдём ко второму действию.

Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.

Легло построить аналогичные алгоритмы для задач

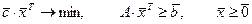
На практике описанный алгоритм реализуется с помощью таблиц.

Пример. Необходимо решить задачу оптимизации плана производства с целью получения максимальной прибыли. Исходные данные приведены в табл.

					Таблица 1.4.
Ресурсы					Запас ресурсов
Трудовые
Сырье
Оборудование
Прибыль
План

Математическая модель задачи примет вид:

,

(*)

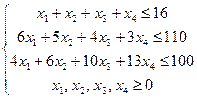Решение. Приведем исходную задачу к каноническому виду. Для этого в ограничения задачи введём дополнительные переменные 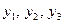и от системы неравенств (*) перейдём к равенствам (**):

(**)

В нашем случае положение исходной вершины многогранника, ограничивающего область допустимых решений, очевидно: 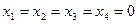. Это переменные — свободные, переменные 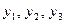— базисные. При 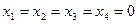получим .

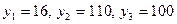Составим первую симплекс-таблицу. Здесь в столбцах, отведённых свободным переменным, в первых трех позициях стоят соответствующие им коэффициенты из (*), в последней индексной строке стоят соответствующие им коэффициенты из выражения целевой функции с противоположным знаком (табл. 1.5).

Таблица 1.5.

Базис	Свободные члены	Свободные переменные
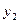
Индексная строка		-60	-70	-120	-130

в начальной вершине с координатами

Для построения следующей таблицы, т.е. переходу к более оптимальной соседней вершине многогранника, выполняем следующие действия:

1). Выбираем наименьший элемент в позициях индексной строки, соответствующих свободным переменным (этот элемент должен быть отрицательным, если он нулевой или положительный, то максимум функционала уже достигнут), в нашем примере: .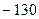

2). Положение этого элемента в индексной строке определяет входящую свободную переменную, в нашем примере , которая переместится в базис и соответствующий столбец, «ключевой столбец», в нашем примере . Символ означает операцию транспонирования.

3). Компоненты вектора свободных членов, в нашем примере , делятся на положительные элементы «ключевого столбца», у нас получится:

.

4). Базисная переменная в строке, которую назовём «ключевой строкой» и которая соответствует наименьшему полученному в пункте 3) компоненту, в нашем примере , выводится из базиса (становится выходящей) и заменяется свободной переменной из пункта 2), в нашем примере .

5). На пересечении ключевых строки и столбца находится разрешающий элемент, в нашем примере это , с помощью которого мы получим очередную симплекс-таблицу. Для этого:

- каждый элемент ключевой строки поделим на разрешающий элемент, получим , на месте разрешающего элемента окажется 1.

- от оставшихся строчек отнимаем преобразованную ключевую, умноженную на коэффициент, подобранный так, чтобы все оставшиеся элементы ключевого столбца стали равны нулю (классическая схема Гаусса получения нулей при эквивалентном преобразовании матрицы).

Процесс построения таблиц продолжаем до тех пор, пока в индексной строке все элементы станут неотрицательными.

Вторая симплекс-таблица будет иметь вид (табл. 1.6).

Таблица 1.6.
Базис	Свободные члены	Свободные переменные на данном шаге: , , и .
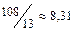
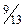
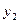
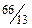
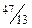
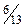
Индексная строка		-20	-10	-20

В базис переместится переменная , ключевая строка первая, выходящая переменная , разрешающий элемент 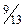,ключевой столбец 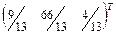. Получим третью симплекс-таблицу (1.7).

Таблица 1.7.
Базис	Свободные члены	Свободные переменные на данном шаге: , , и .
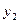
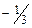
Индексная строка

В базис переместится входящая переменная , ключевая строка третья, выходящая переменная . В индексной строке один из элементов отрицательный, продолжаем алгоритм.

Четвёртая симплекс-таблица имеет вид:

Таблица 1.8.
Базис	Свободные члены	Свободные переменные на данном шаге: , , и .
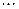
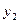
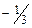
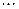
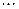
Индексная строка

В индексной строке все элементы положительны, все свободные члены положительны, следовательно, полученное решение оптимально и допустимо.

Оптимальное значение целевой функции достигается в точке , значения базисных переменных равны свободным членам, значения свободных переменных равны нулю.

Заметим, что оптимизация целевой функции достигается при полном использовании трудовых ресурсов и оборудования, излишки сырья составляют 26 единиц, так как .

При использовании симплекс-метода могут возникнуть особые случаи.

1. Вырожденность.

2. Альтернативные решения.

3. Неограниченные решения.

4. Отсутствие допустимых решений.

С этими случаями можно ознакомиться самостоятельно, используя приведенную литературу, например [Таха].