 |
Главная |
Универсальная формула для определения перемещений
|
из
5.00
|
1.1.Начало возможных перемещений.
Теорема Кастильяно открывает принципиальный путь для определения перемещений. Но удобнее использовать другую возможность.
Для этого вспомним известное из курса теоретической механики начало возможных перемещений: если на тело действует уравновешенная система сил, то сумма работ всех этих сил на любых бесконечно малых возможных перемещениях равна нулю.
Начало возможных перемещений применимо как к недеформируемым, так и к деформируемым системам. Применяя начало к деформируемым системам нужно помнить:
1)равновесие должно быть обеспечено в каждой точке; поэтому вычисление виртуальных работ нужно проводить не для всего тела в целом, а в каждой точке;
2) в деформируемом теле работают не только внешние, внутренние силы;
3) возможны только те перемещения, которые допускаются как внешними, так и внутренними силами.
Итак, на основе начала возможных перемещений можно записать
V + W = 0 ((1.8)
1.2. Формула Мора
Не уменьшая общности постановки задачи, найдем прогиб в раме в точке 1 по направлению i – i от заданной обобщенной нагрузки Р (рис.8.1а).

|
Рассмотрим два состояния этой стержневой системы .
Первое состояние – это действительное состояние системы, которая под заданной нагрузкой деформируется и в ней возникают внутренние усилия. Будем придавать Рис.8.1
этим усилиям индекс p: Mp, Qp и Np . Искомому перемещению придадим два индекса  : первый индекс i означает направление перемещения, второй индекс р – причину, вызывающую это перемещение.
: первый индекс i означает направление перемещения, второй индекс р – причину, вызывающую это перемещение.
Второе состояние системы, которое назовем вспомогательным, возникает от действия силы Р = 1 , приложенной в точке 1 по направлении. i – i. В этом состоянии в раме возникают внутренние усилия, которым придадим индекс i : Mi, Qi и Ni .
Рассматривая первое состояние как возможное для второго состояния, на основе начала возможных перемещений можно записать
 = 0 (2.8)
= 0 (2.8)
Отсюда следует формула для определения искомого перемещения

 (3.8)
(3.8)
Формула (3.8) носит название формулы Мора и служит основным инструментом для определения перемещений в стержневых системах.
Эта формула прекрасно “работает” и в случае, когда необходимо найти не линейное, а угловое перемещение какого либо сечения или узла расчетной схемы. В этом случае по направлению искомого угла поворота прикладывают не силу Р = 1, а единичный изгибающий момент М = 1.
В практических расчетах формула (3.8) в полном объеме обычно никогда не используется.
При расчете шарнирно стержневых систем, нагруженных в узлах,( в фермах, например,) возникают лишь одни продольные усилия, а моменты и поперечные силы отсутствуют. Поэтому перемещения в таких системах вычисляются по формуле
 (4.8)
(4.8)
Так как продольные усилия в таких системах постоянны по длине стержней, а жесткость на растяжение-сжатие EA, как правило, тоже постоянна, то формула получает такой простой вид
 (5.8)
(5.8)
В схемах, работающих в основном на поперечную нагрузку, перемещения связаны, главным образом, с изгибанием стержней. Поэтому для них с большой степенью точности можно пренебречь влиянием продольных и поперечных сил на перемещения.
Тогда для определения перемещений в формуле (3.8) можно ограничиться только вторым членом
 (6.8)
(6.8)
Эта формула, которую в строительной механике называют интегралом Мора, и служит для определения перемещений возникающих под нагрузкой в различных стержневых системах (балках рамах).
Покажем, например, как воспользоваться интегралом Мора в известной задаче об определении перемещения конца равномерно нагруженной консоли (рис.8.2)  (7.8)
(7.8)

|
Получен хорошо известный из сопротивления материалов результат. Техника определения перемещений.
2.1.Способ Верещагина
Вычисление перемещения по формуле (6.8) существенно затрудняется, когда система состоит из нескольких по-разному ориентированных в заданной системе координат стержней. Это связано с затруднениями в аналитической записи моментов на разных участках схемы.. Рис.8.2

|
Вычисление интеграла Мора значительно упрощается, если применить способ “перемножения эпюр”, предложенный студентом Верещагиным в 1925 году.
Пусть на каком-то участке системы  заданы две эпюры: Мр и М1 (рис.8.3). Предположим также, что жесткость на изгиб стержня на этом участке постоянна :
заданы две эпюры: Мр и М1 (рис.8.3). Предположим также, что жесткость на изгиб стержня на этом участке постоянна :
EI = const.
Из чертежа видно, что
М1 =  . (8.8) Рис.8.3
. (8.8) Рис.8.3
Интеграл (8.6) после подстановки примет вид
 (9.8)
(9.8)
Здесь  = Мз dx - дифференциал площади эпюры Мр , а произведение
= Мз dx - дифференциал площади эпюры Мр , а произведение  - статический момент этой элементарной площади относительно оси 0 – 0. Сам же интеграл
- статический момент этой элементарной площади относительно оси 0 – 0. Сам же интеграл 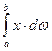 - это статический момент всей площади эпюры Мр относительно оси
- это статический момент всей площади эпюры Мр относительно оси
0 – 0, равный, как известно, всей площади эпюры Мр на участке  , умноженной на расстояние xc от оси 0 – 0 до центра тяжести фигуры (точка ц.т.) Следовательно, результат интегрирования по формуле (9.8) можно представить в виде (10.8). В окончательной формуле использовано следующее из чертежа равенство
, умноженной на расстояние xc от оси 0 – 0 до центра тяжести фигуры (точка ц.т.) Следовательно, результат интегрирования по формуле (9.8) можно представить в виде (10.8). В окончательной формуле использовано следующее из чертежа равенство  .
.
 (10.8)
(10.8)
Итак, результат перемножения эпюр на участке a – b равен произведению площади криволинейной эпюры на ординату прямолинейной эпюры, взятую под центром тяжести площади криволинейной эпюры..
Так как строители строят эпюры моментов “со стороны растянутых волокон”,то указанное правило трансформируется в более простое: если площадь одной “перемножаемой” эпюры и ордината по ее центром тяжести другой эпюры лежат по одну сторону от стержня, то результат “перемножения” – с плюсом, если по разные стороны – с минусом.
Еще раз подчеркнем: если на каком- либо участке одна из эпюр криволинейна (а это может быть только на участке системы, на котором действует распределенная нагрузка), то обязательно нужно брать площадь этого участка. Это следует из вывода правила Верещагина. Если на участке обе эпюры прямолинейны, то площадь можно брать на любой из них.
Применяя способ Верещагина, нужно уметь определять площади сложных фигур и знать положение их центра тяжести. Самую сложную эпюру моментов от обычно встречающихся нагрузок (сосредоточенных сил и моментов, равномерно распределенной нагрузки) всегда можно представить в виде комбинации простых
фигур: прямоугольника, треугольника и квадратной параболы (см. таблицу 1).

|
На рис.8.4, например, показано, как представить эпюру в виде трех простейших составляющих. Результат умножения эпюры Мр на эпюру М1 (рис.8.4е) получается как сумма произведений площадей каждой из составляющих на ординаты под их центрами тяжести из эпюры М1.






 =
=  (11.8)
(11.8) 








|

Рис.8.4
Перемножение эпюр на таких относительно сложных участках удобнее проводить, применяя формулу Симпсона для приближенного численного интегрирования, дающую точный результат, когда обе эпюры прямолинейны и если одна из эпюр очерчена по квадратной параболе (рис.8.5a).
 (12.8)
(12.8)
Если на рассматриваемом участке обе эпюры прямолинейны (умножается трапеция на трапецию,рис.8.5b, то ,разбивая трапеции на простейшие фигуры и применяя способ Верещагина, можно получить удобную формулу
 ) (13.8)
) (13.8)
Применяя формулы (12.8) и (13.8), следует помнить, что если ординаты перемножаемых эпюр лежат по разные стороны от оси стержня, то результат их перемножения нужно брать с минусом.
a)

 b)
b)
Рис.8.5
2.2 Порядок вычисления перемещений без применения ЭВМ.
1. Строят эпюру МР – эпюру изгибающих моментов от заданной нагрузки.
2. Строят эпюру Мi.
Если ищут линейное перемещение, то эпюру Мi строят от единичной силы Р=1, приложенной вдоль линии искомого перемещения. Направление выбирается произвольно. Если результат получается со знаком минус, то это означает, что перемещение имеет направление. обратное выбранному.
Если ищут угол поворота сечения или узла, то эпюру Мi строят от единичного сосредоточенного момента, приложенного в этом сечении или в узле. Направление момента также выбирается произвольно.
3.Вычисляют перемещение по способу Верещагина.
Сравнивая эпюру МР и эпюру Мi , разбивают раму на участки так, чтобы на каждом участке обе эпюры были бы прямолинейны или одна из эпюр – прямолинейна, а другая – гладкая кривая.
“Перемножают” эпюры по способу Верещагина или, применяя при необходимости формулы (12.8) и (13.8) на каждом из выбранных участков. Сложив результаты вычислений на всех участках, получают искомое перемещение.
Если результат получается со знаком минус, то это означает, что рассматриваемая точка (или сечение) будет перемещаться в направлении, противоположном принятому в начале расчета.
2.3 Вычисление перемещений при помощи матриц.
Определение перемещений в статически определимых системах – трудоемкая задача, связанная с утомительными алгебраическими выкладками. Применение ЭВМ существенно облегчает и ускоряет получение результата. Формулу Симпсона (12.8) легко представить в матричном виде , что особенно удобно при использовании стандартных программ.
Элементарные сведения о матрицах приведены в Приложении.
Используя правила перемножения матриц (стр. 3 – 4 Приложения), формулу (12.8) можно получить, проделав следующие действия над тремя матрицами

 ( 16.8 )
( 16.8 )
В компактном виде выражение ( 16.8) может быть записано так
 ( 17.8 )
( 17.8 )
 (18.8)
(18.8)
= матрица-строка из ординат эпюры изгибающих моментов от единичного воздействия в начале, середине и конце участка соответственно,
 ( 19.8 )
( 19.8 )
- матрица податливости рассматриваемого элемента,
 =
=  (20.8)
(20.8)
- матрица-столбец (вектор) из ординат изгибающих моментов от внешней нагрузки в начале , середине и конце участка соответственно.
Если на участке рамы обе эпюры МР и М1 прямолинейны, то матрицы  и
и  имеют более простой вид
имеют более простой вид
 (21.8)
(21.8)
 (22.8)
(22.8)
 (23.8 )
(23.8 )
Выражение (17.8 ) позволяет найти часть перемещения  , как результат “перемножения” эпюр на участке рамы, где эпюра МР –гладкая кривая, а эпюра Мi прямолинейна ( как на рис.8.5а).
, как результат “перемножения” эпюр на участке рамы, где эпюра МР –гладкая кривая, а эпюра Мi прямолинейна ( как на рис.8.5а).
Если обе эпюры прямолинейны, то в формуле 17.8 матрицы имеют вид (20.8), (21.8) и (22.8).
Если ищут перемещение в системе, в которой можно указать n таких участков (или стержней), то оно определяется как сумма
 (24.8 )
(24.8 )
где 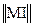 Т =
Т =  (25.8)
(25.8)
- матрица-строка из ординат эпюры Mi на всех участках рамы,
 (26.8)
(26.8)
- матрица –столбец из ординат эпюры MP  на всех участках рамы,
на всех участках рамы,
 квазидиагональная матрица податливости всей системы, имеющая вид
квазидиагональная матрица податливости всей системы, имеющая вид











 ( 27.8 )
( 27.8 )

Порядок этой матрицы зависит от числа элементов ( участков), на которые разбивается рама.
Если в заданной раме от заданной нагрузки определяется несколько перемещений ( например, i=1,2), то матрица 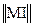 Т (25.8 ) будет иметь столько строк, сколько определяется перемещений
Т (25.8 ) будет иметь столько строк, сколько определяется перемещений
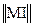 Т=
Т=  (28.8 )
(28.8 )
Поскольку элементы рамы связаны между собой, то можно понизить порядок матрицы податливости  .
.
Если на границе участков к и к+1 непрерывны как единичные, так и грузовая эпюры (значение ординаты эпюры моментов в конце одного участка равно ординате эпюры моментов в начале примыкающего участка, что может иметь место при стыковке только двух стержней) то нижняя строка матрицы  совмещается с верхней строкой матрицы
совмещается с верхней строкой матрицы  , а правый столбец матрицы
, а правый столбец матрицы  совмещается с левым столбцом матрицы
совмещается с левым столбцом матрицы  . Такой сдвиг матриц условно показан на схеме ( 28.8 )
. Такой сдвиг матриц условно показан на схеме ( 28.8 )






 ( 29.8)
( 29.8)
2.4 Порядок вычисления перемещений на ЭВМ.
1. Строят эпюру МР от заданной нагрузки.
2. Строят эпюры Мi от силы Р=1, приложенной по направлению искомого перемещения, или от единичного момента m=1, если ищут угол поворота сечения. Отдельно строят столько эпюр Мi ,сколько нужно найти перемещений.
3. Сравнивая эпюру МР и все эпюры Мi , разбивают раму на участки так, чтобы на каждом участке эпюры были гладкими кривыми или прямолинейными (без переломов и скачков). Нумеруют концы выделенных участков, определяют точки ввода данных.
На этом этапе устанавливают знаки для моментов. Все эпюры построены на растянутых волокнах. Знаки устанавливаются произвольно для того, чтобы дать команду машине с какой стороны стержня( слева или справа,сверху или снизу ) расположена эпюра в расчетной точке.
4. Составляют матрицы 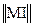 и
и  , придавая значениям моментов в точках ввода те знаки, которые заданы при выполнении п.3.
, придавая значениям моментов в точках ввода те знаки, которые заданы при выполнении п.3.
5. Составляют матрицы податливости для всех выделенных участков, используя выражения ( 19.8) и ( 23.8 ).
6. Формируют матрицу податливости для всей рамы, помня о правиле (29.8 ).
7. Вводят матрицы 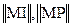 и
и  в ЭВМ, руководствуясь указаниями на дисплее.
в ЭВМ, руководствуясь указаниями на дисплее.
8. Проверяют и корректируют (если необходимо) введенные данные, руководствуясь указаниями на дисплее.
9. Нажимают клавишу ENTER, получают на дисплее искомые перемещения.
Примечание: Программа составлена для учебных задач, в которых число расчетных точек не превышает 11.
|
из
5.00
|
Обсуждение в статье: Универсальная формула для определения перемещений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

