Ортогональные прямозубые конические зубчатые передачи

Наибольшее распространение имеют конические передачи с прямы­ми и криволинейными зубьями; крайние равномерно вытесняют переда­ли с тангенциальными зубьями. Конические зубча­тые колеса с криволинейными зубьями могут иметь круговую, эвольвентную и циклоидальную линию зубьев; более всераспространенные колеса с круговыми зубьями. Углы делительных конусов ортогональных передач просто определя­ются в зависимости от числа зубьев ведущего и ведомого колес, а следо­вательно, от передаточного числа передачи:

tgδ₁ = d₁/d₂ = z₁/z₂ = 1/u либо u = ctg δ₁, = tg δ₂.

Ширину зубчатого венца b по эталону рекомендуется принимать

b ≤ 0,3R_e либо b ≤ < 10 m_e ;

вычисленное значение округляется до целого числа, а при проектирова­нии обычных редукторов значения b принимаются по эталону. Не считая ширины венца b указанный эталон на ортогональные кони­ческие передачи для редукторов устанавливает номинальные значения
наружного делительного поперечника колеса d_e2 (в основном определяющего
габариты редуктора) и номинальные значения передаточных чисел и (от u = 1
до u = 6,3, см. табл. 7.5). В приложении к ГОСТу имеется таблица, в ко­торой для каждого обычного значения передаточного числа и указаны взаимносогласованные значения d_e и b.

Для прямозубых конических передач рекомендуется и u ≤ 3,

Основные сведения о передаче Новикова.

Зубчатые передачи с зацеплением M.Л. Новикова

В этом зацепле­нии профиль зубьев выполняется не по эвольвенте, а по дуге окружности или по кривой, близкой к ней

При зацеплении выпуклые зубья одного из колес контактируют с вогнуты­ми зубьями другого. Поэтому площадь соприкосновения одного зуба с другим в передаче Новикова значительно больше, чем в эвольвентных передачах. Касание сопряженных профилей теоретически происходит в точке, поэтому данный вид зацепления называют точечным.

При одинаковых с эвольвентным зацеплением параметрах точечная систе­ма зацепления с круговым профилем зуба обеспечивает увеличение контакт­ной прочности, что в свою очередь позволяет повысить нагрузочную способ­ность передачи в 2...3 раза по сравнению с эвольвентной. Взаимодействие зу­бьев в сравниваемых передачах также различно: в эвольвентном зацеплении преобладает скольжение, а в зацеплении Новикова — качение. Это создает благоприятные условия для увеличения масляного слоя между зубьями, уменьшения потерь на трение и увеличения сопротивления заеданию.

К достоинствам зацепления Новикова относятся возможность примене­ния его во всех видах зубчатых передач: с параллельными, пересекающи­мися и скрещивающимися осями колес, с внешним и внутренним зацепле­нием, постоянным и переменным передаточным отношением. Потери на трение в этой системе зацепления примерно в 2 раза меньше потерь в эвольвентном зацеплении, что увеличивает КПД передачи.

К основным недостаткам передач с зацеплением Новикова относятся: технологическая трудоемкость изготовления колес, ширина колес должна быть не менее 6 модулей и др. В настоящее время передачи с зацеплением Новикова находят применение в редукторах больших размеров.

Планетарные передачи.

Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Планетарную передачу применяют как редуктор с постоянным передаточным числом, как коробку скоростей, передаточное число в которой изменяется путём поочерёдного торможения различных звеньев (водила или одного из колёс), как дифференциальный механизм. Их успешно применяют в транспортном машиностроении, станкостроении, приборостроении и т.д. Имеется большое количество различных типов планетарных передач, но одноступенчатая планетарная передача (рис. 1) получила самое широкое распространение. Она с успехом применяется как для больших, так и малых мощностей в силовых и кинематических приводах, т.е. не имеет ограничений по применению. КПД передачи 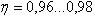. В передачах применяют не только цилиндрические, но и конические колёса. Зубья могут быть прямые и косые. Обычно число сателлитов С=3…6, но встречаются передачи с С>6. Наибольшее распространение получили прямозубые передачи с числом сателлитов С=3.

4.7.2 Устройство и принцип работы

Планетарная передача (рис. 2.3.21) состоит из неподвижного центрального колеса 1с наружными зубьями, сателлитов2, неподвижного центрального колеса 3 с внутренними зубьями и водила Н, на котором укреплены оси сателлитов.

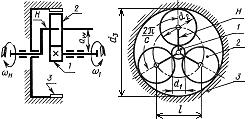
Рисунок 2.3.21 Простейшая планетарная передача

Сателлиты обкатываются по центральным колесам и вращаются вокруг своих осей, то есть совершают движение, подобное движению планет. Водило вместе с сателлитами вращается вокруг центральной оси.

При неподвижном центральном колесе 3 движение может передаваться от центрального колеса1 к водилу Н или от водила к колесу1. В случае неподвижного водила движение может передаваться от колеса1 к колесу3 или от колеса 3 к колесу 1.

Планетарную передачу, в которой одно из центральных колёс неподвижно, называют простейшей. В отличие от простейшей планетарную передачу, в которой все зубчатые колёса и водило подвижны (свободны), называют дифференциальной. В дифференциальной передаче одно движение можно раскладывать на два или два движения сложить в одно. Например, движение колеса 3 можно передавать одновременно колесу 1 и водилу Н или от колес 1 и 3 водилу Н.

4.7.3 Достоинства планетарных передач

1) Большое передаточное число в одной ступени;
2) Малые габариты и масса. Это объясняется следующим: мощность передается по нескольким потокам, число которых равно числу сателлитов;
3) Повышенная нагрузочная способность, так как широко применяются зубчатые колёса с внутренним зацеплением (большой радиус кривизны);
4) Малая нагрузка на опоры, так как сателлиты расположены симметрично, и поэтому силы в передаче взаимно уравновешивают друг друга;
5) Планетарные передачи работают с меньшим шумом, что связанно с повышенной плавностью внутреннего зацепления и меньшими размерами колёс.

4.7.4. Недостатки планетарных передач

1) Повышенные требования к точности изготовления и монтажа;
2) Резкое снижение КПД передачи с увеличением передаточного числа (увеличение количества трущихся поверхностей).

4.7.5. Разновидности планетарных передач

Существует большое количество планетарных передач. Выбор типа передач определяется ее назначением. Наиболее широко в машиностроении применяется однорядная передача (рис.2.3.21). Эта передача имеет минимальные габариты. Она применяется в силовых и вспомогательных приводах. К.п.д. = 0,96-0,98 при и=3,15-12,5. Для получения больших передаточных чисел применяют многоступенчатые планетарные передачи (рис.2.3.22).

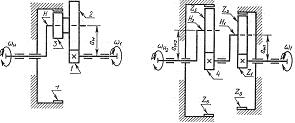
Рисунок 2.3.22 Многоступенчатые планетарные передачи

4.7.6. Конструктивные особенности планетарных передач

Вследствие неизбежной неточности изготовления и сборки зубчатых колес планетарной передачи нагрузка между сателлитами распределяется неравномерно. Для выравнивания нагрузки по потокам одно из центральных колес делают самоустанавливающимся, то есть не имеющим радиальных опор.

Водила планетарных передач должны быть прочными и жесткими при малой массе. Их изготавливают литыми из высокопрочного чугуна.

Подбор чисел зубьев планетарной передачи основывается на трех условиях:
1) Условие соосности, по которому межосевые расстояния зубчатых пар с внешним и внутренним зацеплением должны быть равны. При этом число зубьев центральной шестерни задают из условия неподрезания ножки зуба, а число зубьев внешнего колеса – по заданному передаточному отношению.
2) Условие сборки - во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, иначе собрать передачу невозможно.
3) Условие соседства – сателлиты при вращении не должны задевать друг друга зубьями.

17. Кинематика планетарных передач.

Инематика.

При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса. Всей планетарной передаче .мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм (рис. 8.45, β), представляющий собой простую передачу, в которой движение передается οτακί через паразитные колеса g. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. В качестве примера проанализируем кинематику передачи, изображенной на рис. 8.45. Условимся приписывать частотам вращения индекс звена (<па, nh и т. д.), а передаточные отношения сопровождать индексами в направлении движения и индексом неподвижного звена. Например, ibah означает передаточное отношение от А к А при неподвижном Ь. Для обращенного механизма

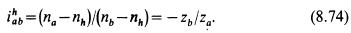
В планетарных передачах существенное значение имеет знак передаточного отношения. Условимся, что при />0 вращение ведущего и ведомого звеньев происходит в одном направлении; при /<0 вращение противоположное. В рассматриваемом примере колеса а и b вращаются в разных направлениях, а потому ihab<0.
Переходя к реальному механизму, у которого в большинстве случаев практики колесо b заторможено, а — ведущее и h — ведомое, на основе формулы (8.74) при пъ = 0 получаем

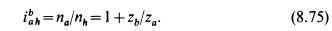
Частоту вращения сателлита определим из равенства

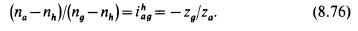
При заданных па и nh определяют пд или (ng — nh) как частоту вращения сателлита относительно водила или относительно своей оси (используют при расчете подшипников).
Далее,

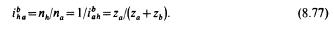
Для случая, когда неподвижно колесо я, на основе формулы (8.74) при ив = 0 с помощью аналогичных преобразований находим

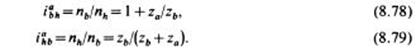
Анализ кинематики планетарных передач, выполненных по другим схемам, производят таким же методом.
Силы в зацеплении. Из рис. 8.46 ясно, что, по условиям равновесия сателлита,

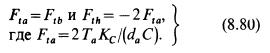
Здесь С—число сателлитов; Кс — коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами.
Радиальные и осевые нагрузки при известной окружной силе определяют так же, как и в простых передачах

18. Условия подбора чисел зубьев планетарных передач.

Подбор чисел зубьев планетарной передачи основывается на трех условиях:
1) Условие соосности, по которому межосевые расстояния зубчатых пар с внешним и внутренним зацеплением должны быть равны. При этом число зубьев центральной шестерни задают из условия неподрезания ножки зуба, а число зубьев внешнего колеса – по заданному передаточному отношению.
2) Условие сборки - во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, иначе собрать передачу невозможно.
3) Условие соседства – сателлиты при вращении не должны задевать друг друга зубьями.