Явление электромагнитной индукции

Энергия магнитного поля

 

Основные формулы

 

1. Закон Фарадея для электромагнитной индукции

2. Максвелловская формула явления электромагнитной индукции

где S – произвольная поверхность, опирающаяся на контур l.

 

3. ЭДС индукции в движущемся проводнике

4. ЭДС индукции во вращающемся проводнике

 

5. Переменная ЭДС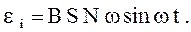

 

6. Самоиндукция

7. Взаимная индукция .

8. Коэффициент самоиндукции и взаимной индукции

 

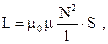
9. Токи замыкания и размыкания цепей

 

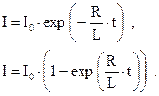
10. Энергия магнитного поля в электрической цепи

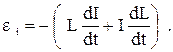11. Объёмная плотность энергии магнитного поля

12. Энергия неоднородного магнитного поля, заключённая в объёме V:

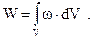
Примеры решения задач

 

Задача 1. Проволочное кольцо радиусом 10 см имеет сопротивление 2 Ом. Какой заряд течёт по кольцу с одинаковой скоростью, если однородное магнитное поле с индукцией 10² Тл быстро изменит своё направление на противоположное?

 

Дано: Решение

r = 10 см = 0,1 м При изменении направления индукции магнитного поля

R = 2 Ом в кольце появится кратковременный индукционный ток

B = 10² Тл за счёт изменения угла между силовыми линиями поля и

q_i - ? нормалью, проведённой к плоскости кольца (рис.7.1).

 

α_ = 0 α_2 = 180⁰.

 

 

 

 

а) б)

Рис.7.1

Магнитный поток сквозь площадь S, ограниченную кольцом:

Изменение магнитного потока

Поскольку α_2 = 180⁰и α_ = 0, то

По закону Фарадея определим ЭДС индукции:

В замкнутой электрической цепи кольца ЭДС индукции вызывает появление индукционного тока, величина которого определяется законом Ома.

В свою очередь сила тока и величина индукционного заряда связаны соотношением

Объединяя формулы (1) – (3), для заряда окончательно получим

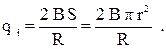
Подставим числовые значения:

 

Задача 2. В однородном магнитном поле с индукцией 0,05 Тл вращается стержень длиной 50 см с угловой скоростью 15 рад/с. Сопротивление стержня 0,5 Ом. Какой силы индукционный ток проходит по стержню, если индукция магнитного поля направлена перпендикулярно плоскости вращения стержня?

Дано: В = 0,05 Тл ω = 15 рад/с l = 50 см = 0,5 м R = 0,5 Ом	Решение При вращении стержня в магнитном поле на его концах появляется разность потенциалов U, равная по модулю ЭДС индукции εi : U = εi . По закону Фарадея
I i - ?

где dФ - мгновенное значение магнитного потока через поверхность dS, пересекаемую стержнем за время dt. dS определим как площадь треугольника (рис.7.2):

B = const

 

Рис.7.2

 

Тогда ЭДС индукции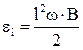

и сила индукционного тока

Подставим числовые значения:

Задача 3. В длинном прямом соленоиде с радиусом сечения 5 см и густотой намотки 200 витков на метр изменяют ток с постоянной скоростью 5 А/с. Найти модуль вектора напряжённости вихревого электрического поля как функцию расстояния от оси соленоида и рассчитать её на расстоянии 3 см от центра.

Дано: n = 200 витк /м r1 = 3 см = 3 . 10-2 м dI / dt = 5 А/с R = 5 см = 5 . 10-2 м	Решение Изменяющийся ток в соленоиде создаёт изменяющееся магнитное поле внутри соленоида, которое в свою очередь порождает вихревое электрическое поле (рис.7.3).
Eвихр (r) - ? E1 - ?

Воспользуемся первым уравнением Максвелла

(1)

где – длина контура интегрирования, S – поверхность, натянутая на контур .

В качестве контура интегрирования выберем окружность радиусом r, тогда векторы E_вихр и dl будут направлены вдоль одной прямой, а величина вектора E_вихр будет одинаковой для всех точек окружности.

 

Рис.7.3 Рис. 7.4

 

С учётом того, что однородное магнитное поле сосредоточено только внутри соленоида, для всех точек, удовлетворяющих условию r < R, имеем

(2)

(3)

Подставим (2) и (3) в выражение (1):

откуда

(4)

Индукция поля в соленоиде

(5)

Подставляя (5) в (4), для напряжённости вихревого электрического поля окончательно получим

(6)

Величина Е_вихр линейно увеличивается при увеличении расстояния r до значения, определяемого из условия (6) при r = R (рис.7.4):

Подставим в числовые значения:

 

Задача 4. Соленоид с индуктивностью 0,1 Гн и сопротивлением 0,02 Ом включен в электрическую цепь (рис.7.5). Сопротивление резистора R = 0,03 Ом, ЭДС источника тока 2 В. Найти количество электричества (заряд), которое пройдет по соленоиду при размыкании ключа К ?

Дано: L = 0,1 Гн R = 0,03 Ом ε0 = 2 В R0 = 0,02 Ом	Решение При разомкнутом ключе К по соленоиду протекает ток I0 = ε0 /R0. При размыкании ключа К ток в соленоиде и обусловленный им магнитный поток начнут уменьшаться.
q - ?
Возникшая в соленоиде ЭДС индукции εi=-dФ/dtсоздаёт индукционный ток I, протекающий по соленоиду и сопротивлению R. Индукционный ток перенесёт количество электричества через соленоид:     Рис. 7.5 (1) Сила электрического тока может быть определена по закону Ома для замкнутой цепи:

(2)

Подставляя (2) в выражение для заряда (1), получаем

С учётом Ф₀ = L ^. I₀ (потокосцепление самоиндукции в начальный момент времени) окончательно находим

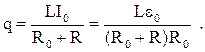
Подставим числовые значения:

 

K

Задача 5. Два концентрических тонких проводника в форме окружностей с радиусами a и b лежат в одной плоскости. Имея в виду, что a<<b, найти: их взаимную индуктивность; магнитный поток, который пронизывает поверхность, натянутую на внешний проводник, когда по внутреннему проводнику течёт ток I.

Дано: a b (a<<b)	Решение Для нахождения взаимной индуктивности воспользуемся выражением, определяющим потокосцепление взаимной индукции:
Lab - ? Фab - ?

где Ф_аb – магнитный поток, сцепленный с контуром a и обусловленный током I_b, протекающим по контуру b (рис.7.6). С другой стороны, магнитный поток может быть вычислен по общему правилу:

.

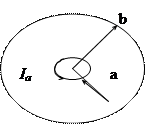Так как a<<b, то значение Bb можно считать постоянным в пределах круга радиусом a, равным индукции в центре кругового тока радиусом b и направленным по нормали к поверхности контура. Учитывая это, получим Рис. 7.6

Отсюда

Для нахождения магнитного потока через поверхность контура b Ф_ab при протекании тока I_a по контуру a воспользуемся тем, что L_ab = L_ba. Тогда

Подставляя значение L_ba и I_a = I, находим

Задача 6. На железный тор намотано 500 витков. Найти энергию магнитного поля, если при токе 2 А магнитный поток через поперечное сечение тора 1 мВб.

 

Дано: N = 500 витк I = 2 А Ф = 1 мВб = 10-3 Вб	Решение Для нахождения энергии магнитного поля учтём, что магнитное поле тороида сосредоточено в пределах железного сердечника, а энергия поля может быть вычислена по объёмной плотности энергии.
W - ?
Рис. 7.7	Выделим элемент объёма в виде прямого цилиндра, расположенного на расстоянии r от центра тороида с образующей d , направленной по касательной к окружности радиусом r и площадью основания dS(рис.7.7). Тогда элемент объёма . Интеграл по объёму тора можно представить в следующем виде:

По теореме о циркуляции вектора Н

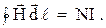
По определению магнитного потока

Используя это, получим

Подставим числовые значения:

 

Задача 7. Ток 10 А течёт по длинному прямому проводнику круглого сечения с магнитной проницаемостью 10³. Найти энергию магнитного поля внутри провода в расчёте на единицу его длины.

 

Дано: I = 10 А μ = 103	Решение Энергию неоднородного поля внутри провода найдём как
- ?
где ω - объёмная плотность энергии, 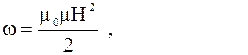(2) а dV –элементарный объём, внутри которого величину ω можно считать постоянной (рис.7.8). , (3) где – длина провода. Напряжённость поля Н на расстоянии r от центра проводника определим по теореме о циркуляции Н, выбрав за контур интегрирования

окружность радиусом r.

.

В нашем случае

где S = πr² – площадь круга радиусом r.

Тогда ,

или . Рис. 7.8 (4)

Подставим формулы (2), (3) и (4) в интеграл (1):

 

Энергия магнитного поля, приходящаяся на единицу длины провода:

Подставим числовые значения: