Научный руководитель – Сотников А. И., к. ф.-м. н., доцент кафедры математического анализа и МПМ

Латентно-структурный анализ – это метод вероятностно-статистического моделирования, идея которого основана на предположении, что наблюдаемое поведение (например, ответы индивидов на вопросы теста/анкеты) есть внешнее проявление некоторой скрытой (латентной) характеристики, присущей индивидам. Задача метода заключается в том, чтобы изучив наблюдаемое поведение индивидов, вывести эту скрытую характеристику и разделить (классифицировать) индивидов по сходству (равенству) ее значений [1].

Цели:

Ø Обработка результатов итогового тестирования в рамках классической теории тестов.

Ø Обработка результатов тестирования на основе современной теории тестов с использованием математического аппарата латентно-структурного анализа.

Суть нормативно-ориентированного теста состоит в сравнении индивидуальных результатов (баллов) испытуемых со среднегрупповыми результатами (баллами).

Автором был составлен итоговый тест смешанного типа (содержащий задания двух типов: открытые – с выбором ответа, и закрытые – без вариантов ответа), состоящий из 30 заданий с преобладанием заданий закрытого типа. Тест был разработан в пяти однотипных вариантах. Ответы на задания оценивались по дихотомной шкале: 1 – «ответ верный», 0 – «ответ неверный».

Тестирование проводилось 28 декабря 2010 г.

Количество и контингент испытуемых: студенты 1 курса 1 группы ФМФ ТывГУ специальности «математика, информатика» в количестве 19 человек.

В результате первичной обработки теста в рамках т. н. классической теории тестов были проведены необходимые вычислительные процедуры и получены первые результаты:

· Краевые значения индивидуальных баллов: 22 (максимальный) и 3 (минимальный):

· Мода: 10

· Дисперсия: 30,92

· Среднее квадратичное отклонение: 5,56

Далее были удалены 8 заданий в связи с их низкой валидностью (точечно-бисериальный коэффициент корреляции) и низким значением номинально-дихотомического коэффициента корреляции (коэффициент корреляции Пирсона) [2].

Переходим к следующему этапу исследования теста в рамках современной теории тестов, основываясь на однопараметрической модели Раша [3].

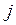
Искомые скрытые характеристики, называемые логитами, мы обозначим следующим образом: пусть параметр отражает уровень подготовленности -го участника тестирования, а параметр – уровень сложности -го тестового задания. Значения этих параметров находятся в результате нескольких этапов вычислений.

Сперва были найдены первичные значения этих параметров как натуральный логарифм отношения долей верных и неверных ответов

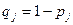
		Доли прав.ответов	Доли неправ.ответов	Логит			Доли прав. ответов	Доли неправ. ответов	Логит
		0,82	0,18	1,5041			0,58	0,42	-0,3185
		0,55	0,45	0,1823			0,84	0,16	-1,674
		0,18	0,82	-1,5041			0,42	0,58	0,3185
		0,82	0,18	1,5041			0,32	0,68	0,7732
		0,18	0,82	-1,5041			0,74	0,26	-1,0296
		0,36	0,64	-0,5596			0,63	0,37	-0,539
		0,05	0,95	-3,0445			0,11	0,89	2,1401
		0,59	0,41	0,3677			0,42	0,58	0,3185
		0,09	0,91	-2,3026			0,26	0,74	1,0296
		0,18	0,82	-1,5041			0,16	0,84	1,674
		0,5	0,5				0,26	0,74	1,0296
		0,32	0,68	-0,7621			0,37	0,63	0,539
		0,23	0,77	-1,2238			0,68	0,32	-0,7732
		0,77	0,23	1,2238			0,11	0,89	2,1401
		0,36	0,64	-0,5596			0,53	0,47	-0,1054
		0,32	0,68	-0,7621			0,32	0,68	0,7732
		0,14	0,86	-1,8458			0,32	0,68	0,7732
		0,73	0,27	0,9808			0,32	0,68	0,7732
		0,36	0,64	-0,5596			0,21	0,79	1,3218
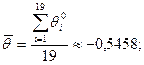
			0,63	0,37	-0,539
		0,37	0,63	0,539
		0,16	0,84	1,674

Следующий шаг – это перевод начальных значений логитов в единую интервальную шкалу стандартных оценок (стандартизация) с использованием следующих формул:

дисперсия по множеству значений .

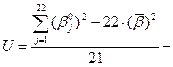дисперсия по множеству значений .

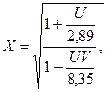
поправочные коэффициенты.

Оценки параметров и в единой интервальной шкале:

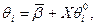
После подсчета имеем:

; ; ;

Таким образом, искомые скрытые характеристики, определяющие результаты тестирования, будут вычисляться по полученным формулам:

; .

Результаты вычисления сведены в таблицу, в которой первый столбец содержит порядковые номера испытуемых, а третий – номера заданий теста после удаления восьми «плохих» заданий:

	Уровень подготовки испытуемого	По возрастанию	№ испытуемых		Уровень трудности заданий	По возрастанию	№ задания
	2,4566	-3,4825			-0,9937	-2,9004
	0,7308	-2,5138			-2,9004	-1,9941
	-1,4712	-1,9174			-0,0979	-1,6334
	2,4566	-1,4712			0,5418	-1,304
	-1,4712	-1,4712			-1,9941	-1,304
	-0,238	-1,4712			-1,304	-0,9937
	-3,4825	-1,1052			2,4644	-0,694
	0,9728	-0,5024			-0,0979	-0,0979
	-2,5138	-0,5024			0,9025	-0,0979
	-1,4712	-0,238			1,8088	0,2124
	0,4927	-0,238			0,9025	0,2124
	-0,5024	-0,238			0,2124	0,5418
	-1,1052	0,4927			-1,6334	0,5418
	2,0906	0,7308			2,4644	0,5418
	-0,238	0,9728			-0,694	0,5418
	-0,5024	1,7734			0,5418	0,9025
	-1,9174	2,0906			0,5418	0,9025
	1,7734	2,4566			0,5418	1,3134
	-0,238	2,4566			1,3134	1,8088
		-1,304	1,8088
	0,2124	2,4644
	1,8088	2,4644

заданий с положительными 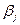больше, чем с отрицательными. Значит, данный тест недостаточно хорошо сбалансирован, он содержит больше трудных заданий, чем легких. Желательно стремиться к тому, чтобы было близко к нулю.

Нахождение числовых значений латентных параметров (логитов) – главный этап в теории латентно-структурного анализа.

Затем вводится величина , называемая надежностью теста, коэффициент которой вычисляется по специальной формуле [4]:

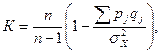где

– коэффициент надежности теста, – число заданий в тесте ( ),

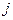доля правильных ответов на - е задание,

дисперсия индивидуальных баллов испытуемых ( ).

Коэффициент надежности исследуемого теста, состоящего из оставшихся 22 валидных заданий, составил 0,9, или 90%. Данный показатель надежности является нормой для нормативно-ориентированных тестов итогового контроля. Коэффициент надежности, имеющий значение в промежутке [0,8; 0,89] неприемлем для итоговых тестов, но вполне приемлем для тестов текущего контроля.

Помимо вышеизложенного вводятся и другие важные величины, характеризующие тест: асимметрия, эксцесс, информационные и вероятностные функции, разрешающая способность теста и др. В данной статье этот материал, в том числе соответствующие «громоздкие» вычисления, мы опускаем.

Вывод: Поставленные цели были достигнуты, была сделана апробация составленного автором нормативно-ориентированного теста и последующая обработка в рамках двух теорий тестов. В результате обработки результатов итогового тестирования следует признать, что исходный составленный тест был недостаточно сбалансирован по трудности заданий, получился слишком трудным для исследуемой выборки учащихся, но, тем не менее, достаточно дифференцирующим тестируемых по степени их подготовки, что и должно соответствовать назначению нормативно-ориентированного теста.

Литература

1. http://mirslovarei.com/content_soc/ANALIZ-LATENTNO-STRUKTURNYJ-6200.html
2. Челышкова М.Б. Теория и практика конструирования педагогических тестов: Учебное пособие. – М.: Логос, 2002. – 432 с.
3. http://www.ldt-tgpi.ru/vocabulary/pon_apparat/test_model_rasha
4. Нейман Ю.М., Хлебников В.А. Введение в теорию моделирования и параметризации педагогических тестов. – М.: 2000. – 168 с.