ПРАКТИЧЕСКОЕ 3АНЯТИЕ № 2 Аналитическое определение количественных характеристик надёжности изделия

 

Теоретические сведения

Выпишем формулы, по которым определяются количественные характеристики надежности изделия:

(2.1), (2.2), (2.3), (2.4), (2.5)

 

где p(t) - вероятность безотказной работы изделия на интервале времени от 0 до t; q(t) - вероятность отказа изделия на интервале времени от 0 до t; f(t) - частота отказов изделия или плотность вероятности времени безотказной работы изделия Т; (t) - интенcивность отказов изделия; m_t - среднее время безотказной работы изделия.

Формулы (2.1) - (2.5) для экспоненциального закона распределения времени безотказной работы изделия примут вид:

 

;	(2.6)
;	(2.7)
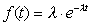;	(2.8)
;	(2.9)
.	(2.10)

 

Формулы (2.1) - (2.5) для нормального закона распределения времени безотказной работы изделия примут вид:

 

;	(2.11)
;	(2.12)
; ;	(2.13)
,	(2.14)

 

где Ф(U) - функция Лапласа, обладающая свойствами

 

Ф(0)=0 ; (2. 15)

 

Ф(-U) =-Ф(U) ; (2.16)

 

Ф()=0.5 . (2.17)

Значения функции Лапласа приведены в приложении П.7.13 [1].

Значения функции (U) приведены в приложении П.7.17 [1].

Здесь m_t - среднее значение случайной величины Т; _t² - дисперсия случайной величины Т; Т- время безотказной работы изделия.

Формулы (2.1) - (2.5) для закона распределения Вейбулла времени безотказной работы изделия имеют вид:

 

;	(2.18)
;	(2.19)
;	(2.20)
;	(2.21)
,	(2.22)

 

где a, k - параметры закона распределения Вейбулла. Г (x) - гамма-функция, значения которой приведены в приложении П.7.18 [1].

Формулы (2.1) - (2.5) для закона распределения Релея времени безотказной работы изделия имеют вид:

;	(2.23)
;	(2.24)
;	(2.25)
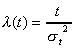;	(2.26)
,	(2.27)

 

где _t - мода распределения случайной величины Т; Т - время безотказной работы изделия.

 

Решение типовых задач

 

Задача 2.1. Время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром =2.510^-5 1/час.

Требуется вычислить количественные характеристики надежности элемента p(t), q(t), f(t), m_t для t=1000час.

Решение. Используем формулы (2.6), (2.7), (2.8), (2.10) для p(t), q(t), f(t), m_t.

1. Вычислим вероятность безотказной работы:

Используя данные таблицы П.7.14 [1] получим

2. Вычислим вероятность отказа q(1000). Имеем

q(1000)=1-p(1000)=0.0247

 

3. Вычислим частоту отказов

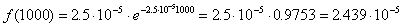; 1/час

4. Вычислим среднее время безотказной работы

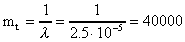час

Задача 2. 2. Время работы элемента до отказа подчинено нормальному закону с параметрами m_t =8000 час, _t =2000 час. Требуется вычислить количественные характеристики надежности p(t), f(t), (t), m_t для t=10000 час.

Решение. Воспользуемся формулами (2.11), (2.12), (2.13), (2.14) для p(t), f(t), (t),m_t.

1. Вычислим вероятность безотказной работы

 

p(t)=0.5Ф(U) ; U=(t-m_t)/_t ;

 

U=(10000-8000)/2000=1; Ф(1)=0.3413 ;

 

p(10000)=0.5-0.3413=0.1587.

2. Определим частоту отказа f(t)

Введем обозначение:

Тогда:

f(t)=(U)/_t ; U=(t-m_t)/_{t ;}

 

f(1000)=(1)/2000=0.242/2000=12.110^-5 1/час.

 

3. Рассчитаем интенсивность отказов (t)

(t)=f(t)/p(t);

 

(10000)=f(10000)/p(10000)=12.110^-5 /0.1587=76.410^-5 1/час.

 

4. Среднее время безотказной работы элемента

m_t = 8000 час.

Задача 2.3. Время работы изделия до отказа подчиняется закону распределения Релея. Требуется вычислить количественные характеристики надежности изделия p(t),f(t),(t),m_t для t=1000час, если параметр распределения _t=1000 час.

Решение. Воспользуемся формулами (2.23), (2.25), (2.27), (2.26) для p(t), f(t),

m_t ,(t).

1. Вычислим вероятность безотказной работы p(t)

2. Определим частоту отказа f(t)

f(t)=tp(t)/_t² ;

f(1000)=10000.606/1000²=0.60610^-3 1/час.

3. Рассчитаем интенсивность отказов

(t)= t/_t ² ;

(1000)=1000/1000² =10^-3 1/час.

4. Определим среднее время безотказной работы изделия

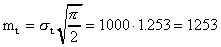час.

Задача 2.4. Время безотказной работы изделия подчиняется закону Вейбулла с параметрами k=1.5; a=10^-4 1/час, а время работы изделия t=100 час. Требуется вычислить количественные характеристики надежности изделия p(t),f(t),(t),m_t.

Решение.

1. Определим вероятность безотказной работы p(t) по формуле (2.18). Имеем:

p(t)=exp(-at^k ); p(100)=exp(-10^-4 100^1.5 ); x=100^1.5 ;

lg x=1,5lg 100=3; x=1000; p(100)=e^-0,1 =0,9048.

2. Определим частоту отказов f(t)

f(t)=akt^k-1 p(t);

f(100)=10^-4 1,5100^0,5 0,90481,3510^-3 1/час.

3. Определим интенсивность отказов (t)

(t)=f(t)/p(t) ;

(100)=f(100)/p(100)=1,3510^-3 /0.90481,510^-3 1/час.

4. Определим среднее время безотказной работы изделия m_t

.

Так как zГ(z)=Г(z+1), то

;

x=10^-2,666 ;lg x=-2,666lg10=-2,666= ; x=0,00215.

 

Используя приложение П.7.18 [1], получим:

m _t =0,90167/0,00215=426 час.

Задача 2.5. В результате анализа данных об отказах аппаратуры частота отказов получена в виде

.

Требуется определить количественные характеристики надежности: p(t), (t),m_t.

Решение. 1. Определим вероятность безотказной работы. На основании формулы (2.1) имеем

Вычислим сумму С₁+ С₂. Так как 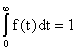, то

.

Тогда

2. Найдем зависимость интенсивности отказов от времени по формуле:

.

 

3. Определим среднее время безотказной работы аппаратуры. На основании формулы (2.5) будем иметь

 

 

Задачи для самостоятельного решения.

Задача 2.6. Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течение 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час, а также среднее время безотказной работы.

 

Задача 2.7. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час, частоту отказов для момента времени t=120 час и интенсивность отказов.

 

Задача 2.8. Время работы изделия подчинено нормальному закону с параметрами

m_t = 8000 час, _t =1000 час. Требуется вычислить количественные характеристики надежности p(t), f(t), (t), m_t для t=8000 час.

Задача 2.9.Время безотказной работы прибора подчинено закону Релея с параметром _t= 1860 час. Требуется вычислить Р(t), f(t), (t) для t = 1000 час и среднее время безотказной работы прибора.

Задача 2.10. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами к=2,6 ; а= 1,65*10^-7 1/час.

Требуется вычислить количественные характеристики надежности Р(t), f(t), (t) для t=150 час. и среднее время безотказной работы шарикоподшипников.

Задача 2.11.Вероятность безотказной работы изделия в течение t=1000 час. Р (1000)=0,95. Время исправной работы подчинено закону Релея. Требуется определить количественные характеристики надежности f(t), (t), m_t.

Задача 2.12. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено закону Релея. Необходимо найти его количественные характеристики надежности P(t), f(t), (t) для t=1000 час.

Задача 2.13. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид

f(t)=2e^-t(1-e^-t). Необходимо найти количественные характеристики надежности P(t), (t), m_t.

Задача 2.14. В результате анализа данных об отказах изделий установлено, что вероятность безотказной работы выражается формулой P(t)=3e^-t-3e^-2t+e^-3t.

Требуется найти количественные характеристики надежности P(t), (t), m_t.

Задача 2.15. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы m_t=1500 час и среднее квадратическое отклонение _t= 100 час.