Испытания при последовательном методе контроля

В основе построения планов испытаний лежит процедура проверки статистических гипотез при последовательном анализе (рис. 2).

Построение планов последовательного контроля и процедура принятия решений при последовательном анализе основаны на вычислении отношения правдоподобия (статистики Вальда)

,

где Р₁ - вероятность получения выборочных значений при условии, что верна гипотеза Н₁ (несоответствие изделий заданным требованиям надежности); Р₀ - вероятность получения выборочных значений при условии, что верна гипотеза Н₀ (соответствие изделий заданным требованиям надежности).

Порядок принятия решений при последовательном анализе:

1) если - принять гипотезу Н₀ (изделия признаются годными);

2) если - принять гипотезу Н₁ (изделия бракуются);

3) если

- продолжить испытания (количество полученной при испытаниях информации недостаточно для вынесения решения о соответствии или несоответствии изделий требованиям надежности по контролируемому показателю).

Рассмотрим построение плана последовательного контроля (рис.7.3) показателя надежности типа Т (наработка) для случая, когда наработка до отказа распределена по экспоненциальному закону. Предусмотрены также планы контрольных испытаний для нормального и логарифмически нормального распределений наработки, распределения Вейбулла и др.

Для случая экспоненциального распределения наработки до отказа функции плотности распределения описываются формулами:

- для группы изделий, соответствующих установленным требованиям по надежности (верна гипотеза Н₀)

; (13)

- для группы изделий, не соответствующих установленным требованиям по надежности (верна гипотеза Н₁)

. (14)

Вероятность появления r отказов в течение суммарной наработки t_∑ может быть подсчитана по формуле распределения Пуассона:

, (15)

где Т - средняя наработка до отказа (на отказ - для восстанавливаемых объектов).

Вероятность получения r отказов при условии, что верна гипотеза Н₁ (несоответствие изделий заданным требованиям надежности):

. (16)

Вероятность получения r отказов при условии, что верна гипотеза Н₀ (соответствие изделий заданным требованиям надежности):

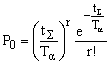. (17)

Отношение правдоподобия

. (18)

Условие приемки дает

. (19)

Логарифмируя (19), получаем

,

откуда после преобразований получаем условие соответствия:

. (20)

Замена знака ≤ на = в неравенстве (20) дает уравнение линии соответствия 2 на плане последовательного контроля (см. рис. 3).

Условие браковки дает

. (21)

Логарифмируя (21), после преобразований получаем условие несоответствия:

. (22)

Заменой знака ≥ на = в неравенстве (22) можно получить уравнение линии несоответствия 1 на плане последовательного контроля.

Усечение плана осуществляется по одноступенчатому методу. Уравнение линии усечения 4 на плане последовательного контроля:

. (23)

Уравнение дополнительной линии соответствия 2' на плане последовательного контроля:

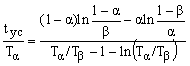. (24)

Уравнение дополнительной линии несоответствия 1' на плане последовательного контроля:

. (25)

При испытаниях без восстановления или замены отказавших изделий минимальный объем выборки N_min = r_ус. При испытаниях с восстановлением или заменой объем выборки может быть любым.

При наличии отрицательных исходов графиком последовательных испытаний является ступенчатая линия 3 (см. рис. 3), сумма отрезков которой, параллельных оси tS / Tα , равна отношению суммарной наработки испытываемых образцов в момент времени t испытаний к значению T_α, а сумма отрезков, параллельных оси r, равна числу отрицательных исходов (отказов) к моменту t.

При отсутствии отрицательных исходов графиком последовательных испытаний является прямая линия с началом в начале координат, совпадающая с осью t_∑/T_α . При этом суммарная наработка испытываемых образцов в момент времени t испытаний составит t_∑ = N_t.

При испытаниях с восстановлением или заменой суммарная наработка в момент времени t испытаний составит

,

где t_j - длительность восстановления работоспособности j-го из r отказавших образцов изделия или длительность замены j-го из отказавших образцов.

При испытаниях без восстановления или замены суммарная наработка в момент времени t испытаний может быть подсчитана по формуле (11).

Результаты испытания положительны, если график испытаний достигает линии соответствия (ступенчатая ломаная линия 3 на рис. 3), и отрицательны, если график достигает линии несоответствия. Если конечная точка графика испытаний находится в области неопределенности между линиями соответствия и несоответствия, то испытания должны быть продолжены (количество полученной при испытаниях информации недостаточно для вынесения решения о соответствии или несоответствии изделий требованиям надежности по контролируемому показателю).