Поверхности второго порядка

Определение.Поверхность, образованная движением некоторой прямой, называемой образующей, вдоль некоторой линии, называемой направляющей, сохраняя постоянное направление, называется цилиндрической поверхностью или цилиндром.

Определение. Цилиндром второго порядка называется цилиндр, направляющая которого является либо окружностью, либо эллипсом, либо гиперболой, либо параболой.

Заметим, что если уравнение

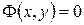
определяет некоторую поверхность, то эта поверхность является цилиндрической с образующей параллельной оси .

Аналогично уравнение

определяет цилиндрическую поверхность с образующей, параллельной оси 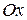, а уравнение

определяет цилиндрическую поверхность с образующей, параллельной оси . Будем рассматривать цилиндрические поверхности, задаваемые уравнениями вида .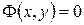

К цилиндрам второго порядка относятся следующие поверхности:

1. эллиптический цилиндр

,

направляющей которого является эллипс, если , и является окружность, если ;

2. гиперболический цилиндр

,

направляющей которого является гипербола;

3. параболический цилиндр

или

,

направляющей которого является парабола.

Определение.Поверхностью вращения называется поверхность, полученная вращением некоторой линии вокруг некоторой оси.

Определение.Поверхностью вращения второго порядка называется поверхность, полученная вращением линии второго порядка вокруг своей оси симметрии.

К поверхностям вращения второго порядка относятся следующие поверхности.

1. Сфера – поверхность, полученная вращением окружности, вокруг ее диаметра. Уравнением сферы, полученной вращением окружности , расположенной на плоскости , вокруг оси , является уравнение

.

2. Эллипсоид – поверхность, полученная вращением эллипса вокруг одной из его осей симметрии. Уравнением эллипсоида, полученного вращением эллипса , расположенного на плоскости , вокруг оси , является уравнение

.

3. Однополостный гиперболоид – поверхность, полученная вращением гиперболы вокруг ее мнимой оси. Уравнением однополостного гиперболоида, полученного вращением гиперболы , расположенной на плоскости , вокруг оси , является уравнение

.

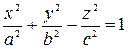4. Двуполостный гиперболоид – поверхность, полученная вращением гиперболы вокруг ее действительной оси. Уравнением двуполостного гиперболоида, полученного вращением гиперболы , расположенной на плоскости , вокруг оси , является уравнение

.

5. Параболоид вращения – поверхность, полученная вращением параболы вокруг ее оси симметрии. Уравнением параболоида, полученного вращением параболы , расположенной на плоскости , вокруг оси , является уравнение

.

6. Конус – поверхность, полученная вращением пары пересекающихся прямых вокруг биссектрисы угла между ними. Уравнением конуса, полученного вращением пары прямых , расположенных на плоскости , вокруг оси , является уравнение

.

 

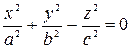Тесты

Приводимые ниже тестовые задания для самоконтроля содержат 50 вопросов. На каждый вопрос приводится три варианта ответа. Лишь один из них правильный.

Критерий выставления оценки по пятибалльной системе предлагается следующий. Студент, давший от 45 до 50 правильных ответов, получает оценку «отлично» (5 баллов). Студент, давший от 35 до 44 правильных ответов, получает оценку «хорошо» (4 балла). Студент, давший от 25 до 34 правильных ответов, получает оценку «удовлетворительно» (3 балла). Студент, давший менее 25 правильных ответов, получает оценку «неудовлетворительно» (2 балла).

 

1. Что не меняется при параллельном переносе прямоугольной декартовой системы координат:

А) Начало координат;

Б) Направление координатных осей;

В) Координаты фиксированной точки.

2. Что меняется при повороте прямоугольной декартовой системы координат:

А) Начало координат;

Б) Единичный отрезок;

В) Направление координатных осей.

3. Если точка делит отрезок пополам, то говорят, что она делит этот отрезок:

А) в отношении ;

Б) в отношении 1;

В) в отношении 2.

4. Полярным радиусом точки в полярной системе координат на плоскости называется:

А) расстояние от этой точки до полярной оси;

Б) расстояние от этой точки до полюса;

В) угол между радиус-вектором и полярной осью.

5. Долготой точки в сферической системе координат называется:

А) полярный угол проекции этой точки на фиксированную координатную плоскость;

Б) полярный радиус проекции этой точки на фиксированную координатную плоскость;

В) расстояние от этой точки до начала координат.

6. Широтой точки в сферической системе координат называется:

А) угол между радиус-вектором этой точки и фиксированной координатной плоскостью;

Б) угол между радиус-вектором этой точки и фиксированной координатной осью;

В) расстояние от этой точки до начала координат.

7. Коллинеарные векторы – это:

А) векторы, лежащие на перпендикулярных прямых;

Б) векторы, лежащие на параллельных прямых;

В) векторы, имеющие одинаковую длину.

8. Что является достаточным условием равенства векторов:

А) равенство их длин;

Б) их коллинеарность;

В) совпадение начальных и конечных точек этих векторов.

9. При умножении ненулевого вектора на число 1 получаем:

А) единичный вектор;

Б) противоположный вектор;

В) исходный вектор.

10. Система трех и более векторов является линейно зависимой тогда и только тогда, когда:

А) один из векторов является нулевым;

Б) два вектора из этой системы являются коллинеарными;

В) один из векторов представим в виде линейной комбинации остальных векторов.

11. В пространстве базисом является:

А) любая тройка компланарных векторов;

Б) любая тройка некомпланарных векторов;

В) любая тройка векторов.

12. Тройка единичных ортов :

А) является правой тройкой векторов;

Б) является левой тройкой векторов;

В) является тройкой компланарных векторов.

13. Скалярное произведение векторов равно:

А) произведению длин этих векторов;

Б) произведению первого вектора на проекцию второго вектора на первый вектор;

В) произведению длин этих векторов на синус угла между ними.

14. Косинус угла между векторами равен:

А) отношению скалярного произведения к произведению длин данных векторов;

Б) отношению длины векторного произведения к произведению длин данных векторов;

В) длине векторного произведения.

15. Если поменять в векторном произведении векторы местами, то:

А) векторное произведение останется прежним;

Б) изменится лишь длина векторного произведения;

В) изменится лишь направление векторного произведения.

16. Длина векторного произведения равна:

А) площади параллелограмма, построенного на данных векторах;

Б) произведению длин данных векторов;

В) произведению длин данных векторов на косинус угла между ними.

17. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда:

А) среди этих векторов есть два коллинеарных вектора;

Б) один из этих векторов ортогонален двум другим векторам;

В) они компланарны.

18. Если в смешанном произведении трех векторов поменять местами два из них, то:

А) смешанное произведение не изменится;

Б) поменяется лишь абсолютное значение смешанного произведения;

В) поменяется лишь знак смешанного произведения.

19. Если подстановка координат любой точки данной линии обращает уравнение 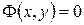в истинное тождество, то это является:

А) лишь необходимым условием того, что 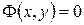- уравнение данной линии;

Б) лишь достаточным условием того, что 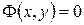- уравнение данной линии;

В) необходимым и достаточным условием того, что 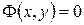- уравнение данной линии;

20. Уравнение при условии :

А) является каноническим уравнением прямой;

Б) является общим уравнением прямой;

В) не является уравнением прямой.

21. Равенство определяет на плоскости:

А) точку с абсциссой ;

Б) прямую параллельную оси абсцисс;

В) прямую параллельную оси ординат.

22. Угловой коэффициент прямой равен:

А) тангенсу угла наклона прямой;

Б) синусу угла наклона прямой;

В) углу наклона прямой.

23. Равенство угловых коэффициентов двух прямых является необходимым и достаточным условием:

А) совпадения этих прямых;

Б) параллельности этих прямых;

В) перпендикулярности этих прямых.

24. В нормальном уравнении прямой 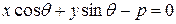параметр 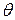равен:

А) углу наклона прямой;

Б) углу наклона прямой, перпендикулярной данной прямой и проведенной из точки ее пересечения с осью абсцисс;

В) углу наклона перпендикуляра, опущенного из начала координат на прямую.

25. В нормальном уравнении прямой 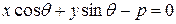параметр 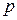равен:

А) расстоянию от начала координат до точки пересечения прямой с осью абсцисс;

Б) расстоянию от начала координат до точки пересечения прямой с осью ординат;

В) расстоянию от начала координат до прямой.

26. При нахождении нормирующего множителя 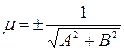для приведения уравнения прямой к нормальному виду знак выбирается:

А) противоположным знаку коэффициента ;

Б) противоположным знаку коэффициента ;

В) противоположным знаку коэффициента .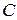

27. Для того, чтобы две точки лежали по одну сторону от данной прямой необходимо и достаточно, чтобы их отклонения от данной прямой:

А) совпадали;

Б) были одного знака;

В) были противоположных знаков.

28. Уравнение является уравнением окружности:

А) с центром в точке ;

Б) с центром в точке ;

В) с центром в начале координат.

29. Любые две точки эллипса удовлетворяют следующему условию:

А) сумма их расстояний до фиксированной точки, называемой фокусом, есть величина постоянная;

Б) сумма их расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная;

В) они равноудалены от фиксированной точки, называемой фокусом.

30. Уравнение является каноническим уравнением:

А) эллипса;

Б) гиперболы;

В) параболы.

31. Фокусы кривой находятся в точках:

А) и ;

Б) и ;

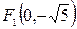В) и .

32. При каком условии эллипс будет более округлым:

А) чем ближе эксцентриситет эллипса к нулю;

Б) чем ближе эксцентриситет эллипса к ;

В) чем ближе эксцентриситет эллипса к единице.

33. Фокальные радиусы точки кривой с эксцентриситетом определяются равенствами

А) , ;

Б) , ;

В) , .

34. Отношение расстояния от произвольной точки эллипса до какого-нибудь фокуса к расстоянию от этой же точки до односторонней с выбранным фокусом директрисы равно:

А) большой полуоси эллипса;

Б) малой полуоси эллипса;

В) эксцентриситету эллипса.

35. Модуль разности расстояний от двух фиксированных точек гиперболы до ее фокусов всегда:

А) меньше расстояния между фокусами;

Б) больше расстояния между фокусами;

В) равен расстоянию между фокусами.

36. однофокусные эллипс и гипербола:

А) не пересекаются;

Б) касаются в двух точках;

В) имеют более двух точек пересечения.

37. Асимптоты гиперболы обладают следующим свойством:

А) они не пересекаются друг с другом;

Б) они не пересекаются с гиперболой;

В) каждая из них касается гиперболы в двух точках.

38. Эксцентриситет гиперболы:

А) всегда меньше единицы;

Б) всегда больше единицы;

В) может быть как меньше единицы, так и больше единицы.

39. При увеличении эксцентриситета гиперболы ее основной прямоугольник:

А) не меняется;

Б) становится ближе к квадрату;

В) становится более вытянутым вдоль оси ординат.

40. Для параболы всегда выполняется условие:

А) расстояние от любой точки параболы до директрисы равно расстоянию от этой точки до фокуса;

Б) для любой точки параболы сумма расстояний до директрисы и до фокуса есть величина постоянная;

В) для любой точки параболы модуль разности расстояний до директрисы и до фокуса есть величина постоянная.

41. Вершина параболы находится в точке:

А) ;

Б) ;

В) .

42. Директрисой параболы является:

А) прямая ;

Б) прямая ;

В) прямая .

43. Уравнение 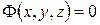в общем случае определяет в пространстве:

А) точку;

Б) линию;

В) поверхность.

44. В пространстве уравнение определяет:

А) плоскость, проходящую через начало координат;

Б) плоскость, параллельную оси абсцисс;

В) плоскость, параллельную оси аппликат.

45. Плоскости и :

А) параллельны;

Б) перпендикулярны;

В) не являются параллельными или перпендикулярными.

46. Какое из следующих уравнений в пространстве является нормальным уравнением плоскости:

А) ;

Б) ;

В) .

47. Угол между прямой и плоскостью в пространстве и угол между направляющим вектором этой прямой и вектором нормали плоскости:

А) равны;

Б) в сумме образуют прямой угол;

В) в сумме образуют развернутый угол.

48. Уравнение 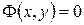определяет в пространстве:

А) цилиндрическую поверхность с образующей параллельной оси абсцисс;

Б) цилиндрическую поверхность с образующей параллельной оси ординат;

В) цилиндрическую поверхность с образующей параллельной оси аппликат;

49. Уравнение 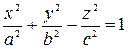определяет в пространстве:

А) однополостный гиперболоид;

Б) двуполостный гиперболоид;

В) конус.

50. Параболоид является:

А) поверхностью вращения первого порядка;

Б) поверхностью вращения второго порядка;

В) поверхностью вращения третьего порядка.

Ответы на вопросы теста

№ вопроса	Правильный ответ	№ вопроса	Правильный ответ
	Б		В
	В		Б
	Б		Б
	А		Б
	А		Б
	Б		В
	Б		А
	В		А
	В		В
	В		А
	Б		В
	А		Б
	Б		Б
	А		В
	В		А
	А		Б
	В		А
	В		В
	А		В
	Б		А
	Б		В
	А		Б
	Б		В
	В		А
	В		Б

Задачи.

1. На оси даны три точки , , . Определить отношение 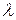, в котором каждая из этих точек делит отрезок, ограниченный двумя другими точками.

2. На оси даны две точки и . Определить координаты точки, симметричной точке относительно точки .

3. В полярной системе координат даны две точки и . Вычислить полярные координаты середины отрезка, соединяющего точки и .

4. В полярной системе координат даны две смежные вершины квадрата и . Определить его площадь.

5. Вычислить площадь правильного треугольника, две вершины которого находятся в точках и .

6. Даны три вершины , и параллелограмма. Найти его четвертую вершину.

7. Даны вершины треугольника , и . Определить длину биссектрисы его внутреннего угла при вершине .

8. Определить координаты концов и отрезка, который точками и разделен на три равные части.

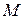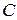9. Точка пересечения медиан треугольника лежит на оси абсцисс, две его вершины – точки и . Третья вершина лежит на оси ординат. Определить координаты точек 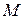и .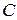

10. На оси ординат найти точку, равноудаленную от точек и .

11. Даны вершины треугольника , и . Вычислить длину биссектрисы его внутреннего угла при вершине .

12. Векторы и образуют угол , причем , . Найти длины векторов и .

13. Выяснить, служат ли точки , , , вершинами трапеции.

14. Даны векторы , и . Проверить, что они образуют базис в пространстве. Найти разложение вектора по этому базису.

15. Векторы и образуют угол , причем , . Вычислить угол между векторами и .

16. Даны вершины четырехугольника , , , . Доказать, что его диагонали и взаимно перпендикулярны.

17. Вычислить внутренние углы треугольника с вершинами , и и выяснить является ли этот треугольник равнобедренным.

18. Вычислить проекцию вектора на ось, создаваемую вектором .

19. Даны точки , и . Вычислить площадь треугольника .

20. Вычислить синус угла, образованного векторами и .

21. Доказать, что точки , , , 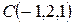лежат в одной плоскости.

22. Вычислить объем тетраэдра, вершины которого находятся в точках , , , .

23. Стороны треугольника лежат на прямых , , 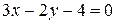. Вычислить его площадь.

24. Дана прямая . Составить уравнение прямой, проходящей через точку , перпендикулярно данной прямой.

25. Даны уравнения двух сторон прямоугольника , и одна из его вершин . Составить уравнения двух других сторон этого прямоугольника.

26. Найти точку, симметричную точке относительно прямой .

27. Составить уравнения прямых, проходящих через вершины треугольника , и параллельно противоположным сторонам.

28. Найти проекцию точки на прямую, проходящую через точки и .

29. Определить угол между прямыми , .

30. Луч света направлен по прямой . Дойдя до прямой , луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

31. Даны две вершины и треугольника и точка пересечения его высот. Составить уравнения сторон этого треугольника.

32. Вычислить отклонение и расстояние от точки до прямой .

33. Выяснить, пересекает ли прямая отрезок, ограниченный точками и .

34. Вычислить расстояние между параллельными прямыми и .

35. Составить уравнение окружности, проходящей через точки и , центр которой лежит на прямой .

36. Установить, какая линия определяется уравнением .

37. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, если расстояние между его директрисами равно 5, а расстояние между фокусами равно 4.

38. Установить, какая линия определяется уравнением .

39. Установить, какая линия определяется уравнением

. Построить ее.

40. Эксцентриситет эллипса равен , фокальный радиус точки равен 10. вычислить расстояние от этой точки до односторонней с этим фокусом директрисы.

41. Определить точки эллипса , расстояние которых до правого фокуса равно 14.

42. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если уравнения ее асимптот , а расстояние между фокусами равно 20.

43. Установить, какая линия определяется уравнением .

44. Установить, какая линия определяется уравнением .

45. Составить уравнение гиперболы, если ее эксцентриситет равен , один из фокусов лежит в точке , а уравнение соответствующей директрисы .

46. Составить уравнение параболы, вершина которой находится в начале координат, если она симметрична относительно оси ординат и проходит через точку .

47. Установить, какая линия определяется уравнением .

48. Составить уравнение параболы, если ее фокус находится в точке , и директриса имеет уравнение .

49. Составить уравнение плоскости, проходящей через точку параллельно векторам и .

50. Установить, перпендикулярны ли плоскости и .

51. Определить угол между плоскостями и .

52. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям , .

53. Вычислить отклонение и расстояние от точки до плоскости .

54. Доказать, что плоскость пересекает отрезок, соединяющий точки и .

55. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей , параллельно вектору .

56. Составить канонические и параметрические уравнения прямой, проходящей через точку параллельно прямой .

57. Даны вершины треугольника , и . Составить параметрические уравнения его медианы, проведенной из вершины .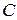

58. Составить канонические уравнения прямой, проходящей через точку параллельно прямой пересечения плоскостей , .

59. Найти острый угол между прямыми и .

60. Найти точку , симметричную точке относительно прямой, проходящей через точки и .

 

 

Литература.

1. Гусак А.А. Высшая математика, т.1. – Мн., 2000.

2. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Мн., 1998.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, 1 часть. – М., 1999.

4. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М., 2003.

5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М., 1985.

6. Письменный Д.Т. Конспект лекций по высшей математике: полный курс. – М., 2006.

7. Шипачев В.С. Высшая математика. – М., 1996.