 |
Главная |
Процесс единичного корня – инструмент проверки нестационарности ВР
|
из
5.00
|
Если  , где
, где  , тогда
, тогда  представляет собой процесс случайного блуждания. Например, стоимость ценной бумаги равна сумме ее цены в предыдущий день торгов и случайного «шока». Случайное блуждание относится к классу нестационарных ВР. Действительно, если начальная цена
представляет собой процесс случайного блуждания. Например, стоимость ценной бумаги равна сумме ее цены в предыдущий день торгов и случайного «шока». Случайное блуждание относится к классу нестационарных ВР. Действительно, если начальная цена  , тогда
, тогда  ,
,  , где
, где  ,
, 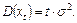
Следовательно, дисперсия  зависит от t. Однако применяя к
зависит от t. Однако применяя к  оператор конечных разностей 1-ого порядка, мы получим стационарный процесс.
оператор конечных разностей 1-ого порядка, мы получим стационарный процесс.
Заметим, что случайное блуждание является процессом авторегрессии 1-ого порядка АР(1):  , где
, где  . Тогда тест проверки нестационарности сводится к проверке условия
. Тогда тест проверки нестационарности сводится к проверке условия  или тесту единичного корня.
или тесту единичного корня.
Вычитая 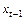 из обеих сторон АР(1), получим:
из обеих сторон АР(1), получим:
 , (9.26)
, (9.26)
где 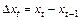 .
.
Тест проверки гипотезы  может быть сведен к проверке
может быть сведен к проверке 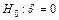 . Так как
. Так как  – стационарен, тогда, если
– стационарен, тогда, если  ,
,  , и
, и  становится стационарным после сглаживания разностью 1-ого порядка.
становится стационарным после сглаживания разностью 1-ого порядка.
В таком случае говорят, что  – интегрируемый процесс 1-ого порядка или I(1). Стационарный процесс обозначается I(0).
– интегрируемый процесс 1-ого порядка или I(1). Стационарный процесс обозначается I(0).
Дики и Фуллер (Dickey-Fuller [26]) показали, что t-статистика для проверки значимости  не следует распределению Стьюдента и смоделировали эмпирическое распределение для:
не следует распределению Стьюдента и смоделировали эмпирическое распределение для: 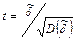 .
.
Тогда решающее правило проверки  имеет вид:
имеет вид:
если 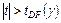 , то следует, что
, то следует, что  неверна и
неверна и  – стационарный ВР,
– стационарный ВР,  – пороговое значение по таблицам Дики-Фуллера;
– пороговое значение по таблицам Дики-Фуллера;
если 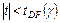 , то
, то  – нестационарный ВР.
– нестационарный ВР.
На практике тест Дики-Фуллера применяют в 3 формах:
 (9.27)
(9.27)
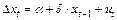 (9.28)
(9.28)
 , (9.29)
, (9.29)
где t – временной тренд.
Заметим, что модели (9.28) и (9.29) характерны для экономических данных.
Процесс коинтеграции
Рассмотрим эконометрическую модель зависимости валового потребления от национального дохода [21]:
 (9.30)
(9.30)
где 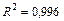 ,
,  .
.
Пусть тест на стационарность указал на то, что 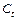 ,
, 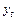 – нестационарные ряды первого порядка I(1). Одинаковый порядок их нестационарности позволяет предположить, что существует линейная комбинация из
– нестационарные ряды первого порядка I(1). Одинаковый порядок их нестационарности позволяет предположить, что существует линейная комбинация из 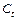 и
и 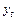 , которая является стационарным ВР.
, которая является стационарным ВР.
Другими словами, даже если 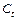 и
и 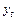 – нестационарные ВР первого порядка I(1), тем не менее существует ВР:
– нестационарные ВР первого порядка I(1), тем не менее существует ВР: 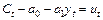 , который является стационарным I(0). Тогда
, который является стационарным I(0). Тогда 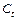 и
и 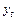 называются
называются
коинтегрирующимися, а  – есть коинтегрирующий параметр. Эта идея может быть распространена на множество переменных, содержащее более чем два ВР.
– есть коинтегрирующий параметр. Эта идея может быть распространена на множество переменных, содержащее более чем два ВР.
Следовательно, коинтегрирующая связь является устойчивой долгосрочной зависимостью между нестационарными ВР одинакового порядка. Экономическими примерами долгосрочных связей являются количественная теория денег, теория перманентного дохода и т.д.
Теория коинтеграции позволяет оценить эту долгосрочную связь, оказывая предпочтение линейным комбинациям нестационарных ВР перед линеаризацией на основе операции разностного сглаживания. Теоретической основой прогнозирования в условиях коинтеграции является теорема представления Гренжера (Granger).
Множество коинтегрированных переменных всегда будет иметь представление в виде модели с корректирующими ошибками (МКО).
Форму МКО проиллюстрируем на следующем примере.
Пусть 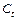 и
и 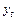 являются нестационарными процессами первого порядка I(1) вида:
являются нестационарными процессами первого порядка I(1) вида:
 , где
, где  (9.31)
(9.31)
 , где
, где 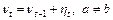 . (9.32)
. (9.32)
Другими словами,  – процесс авторегрессии 1-го порядка,
– процесс авторегрессии 1-го порядка,  – процесс случайного блуждания.
– процесс случайного блуждания.
Приведенная форма зависимости 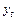 и
и 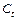 от
от  и
и  имеет вид:
имеет вид:
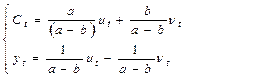
(9.33)
(9.34)
Так как  ,
,  , из (9.33) – (9.34) следует, что
, из (9.33) – (9.34) следует, что 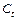 и
и 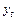 – нестационарные процессы 1-ого порядка I(1). Порядковый критерий идентифицируемости для уравнений (1) и (2) не выполняется, следовательно, невозможно однозначно оценить параметры a и b.
– нестационарные процессы 1-ого порядка I(1). Порядковый критерий идентифицируемости для уравнений (1) и (2) не выполняется, следовательно, невозможно однозначно оценить параметры a и b.
В терминах теории Энгла-Гренжера (Engl-Granger) 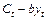 есть коинтегрирующая зависимость, а
есть коинтегрирующая зависимость, а 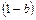 – коинтегрирующий вектор и такая связь – единственная.
– коинтегрирующий вектор и такая связь – единственная.
Применяя операторы конечных разностей для уравнений (9.31) и (9.32) и записывая их в виде системы уравнений, получим:
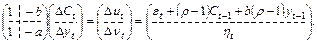 (9.35)
(9.35)
Обращая матрицу коэффициентов при  , имеем:
, имеем:
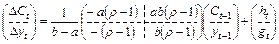 , (9.36)
, (9.36)
где  и
и  – линейные комбинации
– линейные комбинации 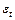 и
и  .
.
Заметим, что если  , то в правой части системы (9.36) исчезает зависимость от
, то в правой части системы (9.36) исчезает зависимость от  и
и  .
.
Пусть  , введем также обозначение
, введем также обозначение  .
.
Тогда модель (9.36) примет вид:

(9.37)
(9.38)
Система (9.37), (9.38) является моделью с корректирующими ошибками, соответствующей исходной модели (9.31), (9.32).
Задача 9.1. Поясните смысл следующих принципиальных понятий:
процесс авторегрессии;
процесс авторегрессии и скользящего среднего;
процесс АРИСС (p, d, q);
стационарность ряда динамики;
автопрогнозирование.
Задача 9.2. Оценка предложения мороженого в зависимости от цены имеет вид:

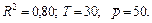
Здесь 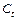 – число проданных порций мороженого в течение месяца t;
– число проданных порций мороженого в течение месяца t;
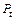 – цена мороженого в период t.
– цена мороженого в период t.
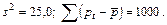
Определите доверительный интервал с надежностью  ,
,
содержащий прогноз сбыта мороженого при цене в 60 тыс. руб.
за порцию.
Задача 9.3. Даны три ряда динамики вида:
а) 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13;
б) 2, 2, 3, 4, 5, 6, 8, 10, 12, 15, 19, 24;
в) 2, 3, 6, 3, 4, 2, 3, 5, 1, 4, 4, 6.
1) Рассчитайте и занесите в таблицу значения:  .
.
2) Исследуйте стационарность анализируемых рядов.
3) Найдите оценку параметра d.
Задача 9.4. Пусть имеются две различные АРИСС (1, 0, 0) модели временного ряда:
Модель А: 
Модель В: 
где 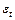 – нормально распределенная случайная величина с нулевым математическим ожиданием и единичной дисперсией.
– нормально распределенная случайная величина с нулевым математическим ожиданием и единичной дисперсией.
1. Определите прогнозы, оптимальные в среднеквадратическом смысле, для периодов Т+1, Т+2, Т+3, если  по обеим моделям.
по обеим моделям.
2. Пусть реальное наблюдение  . Уточните прогнозные значения
. Уточните прогнозные значения 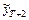 и
и 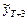 .
.
3.Опираясь на результаты, полученные в предыдущих пунктах задачи, какой модели Вы отдадите предпочтение?
Задача 9.5. Пусть модель, сглаживающая временной ряд 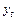 , имеет вид:
, имеет вид:

где 
а) Вычислите  .
.
б) Основываясь на результате пункта а), рассчитайте прогнозы для  и
и  .
.
Задача 9.6. Пусть реальные ежеквартальные данные цен на акции некоторой фирмы имеют вид:
| Год t | Квартал 1 | Квартал 2 | Квартал 3 | Квартал 4 |
| 10,50 | 10,44 | 9,94 | 10,25 | |
| 11,00 | 9,88 | 10,50 | 12,00 | |
| 13,94 | 12,25 | 12,61 | 13,50 | |
| 13,44 | 12,44 | 13,50 | 15,39 | |
| 15,75 | 13,88 | 14,50 | 15,50 | |
| 16,13 | 14,75 | 11,75 | 15,25 | |
| 17,13 | 20,50 | 19,00 | 21,50 | |
| 20,25 | 25,63 | 26,88 | 27,63 | |
| 23,88 | 26,38 | 24,00 | --- |
1. Произведите процедуру выбора оценок параметров p, d и q для построения модели АРИСС (p, d, q) для прогнозирования цены на акции компании.
2. Оцените коэффициенты модели АРИСС (  ).
).
3. Сделайте прогноз цен акции на четыре квартала в будущем.
4. Вычислите относительную погрешность прогноза, если реальные значения цен на акции составили: 
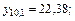
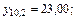
 .
.
Задача 9.7. Пусть для оценивания зависимости цены акции менеджером предложена регрессионная модель, расчет коэффициентов которой по данным задачи 9.6. имеет вид:

где 
Здесь переменными обозначены:
 – цена (в долларах) акции фирмы в квартале t;
– цена (в долларах) акции фирмы в квартале t;
 – индекс Доу-Джонса в квартале t;
– индекс Доу-Джонса в квартале t;
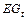 – средний абсолютный прирост активов фирмы за предыдущие 5 лет;
– средний абсолютный прирост активов фирмы за предыдущие 5 лет;
 – объявленные дивиденды (в долларах) к концу квартала t;
– объявленные дивиденды (в долларах) к концу квартала t;
 – стоимость акции фирмы, оцененная бухгалтерией фирмы, в квартале t;
– стоимость акции фирмы, оцененная бухгалтерией фирмы, в квартале t;
1. Оцените значимость коэффициентов модели с доверительной вероятностью  .
.
2. Проанализируйте мультиколлинеарность экзогенных переменных модели.
3. Рассчитайте прогнозы на четыре квартала в будущем и оцените их относительные погрешности, если реальные наблюдения составили 
4. Сравните точности моделей по полученным погрешностям прогнозирования. Какую модель Вы бы предпочли и почему?
Задача 9.8. Предположим, что Вы решили определить прогноз предстоящей подписки на газету, дилером которой являетесь, на основе следующей эконометрической модели:

где 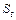 – число подписчиков газеты на квартал t;
– число подписчиков газеты на квартал t;
 – ВНП к началу текущего квартала;
– ВНП к началу текущего квартала;
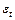 – случайная переменная, следующая стандартному нормальному вероятностному закону.
– случайная переменная, следующая стандартному нормальному вероятностному закону.
Опишите алгоритм построения прогноза 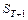 и
и  в трех следующих случаях:
в трех следующих случаях:
а) вам точно известны значения ВНП в предстоящие периоды времени.
б) вы не располагаете точной информацией о значениях  и
и  , однако сумма подписки является незначительной по сравнению с величиной ВНП.
, однако сумма подписки является незначительной по сравнению с величиной ВНП.
в) сумма подписки на газету превышает половину ВНП, а все другие компоненты ВНП представляют собой случайные величины, зависящие от времени.
|
из
5.00
|
Обсуждение в статье: Процесс единичного корня – инструмент проверки нестационарности ВР |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

