Мегаобучалка Главная | О нас | Обратная связь


Двухшаговый метод наименьших квадратов



2015-11-20 594 Обсуждений (0)
Двухшаговый метод наименьших квадратов 0.00 из 5.00 0 оценок




Рассмотрим данный метод на примере для модели IS-LM для закрытой экономики при фиксированной налоговой ставке ( ):

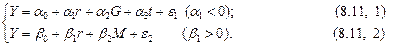
Второе уравнение является переопределенным. Для его оценки рекомендуется использовать двухшаговый метод наименьших квадратов (ДМНК).

 

Шаг 1.

В уравнении переопределенной переменной является процентная ставка . Ее можно оценить, лишь опираясь на экзогенные переменные (например, вычесть из уравнения (8.11, 1) уравнение (8.11, 2)):

(8.12)

 

Коэффициенты 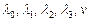предлагается найти самостоятельно по аналогии с ранее рассмотренными примерами.

Применяя для (8.12) МНК, получаем оценку переменной :

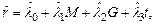(8.13)

 

где – условная средняя при фиксированных значениях .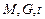

 

Шаг 2.

Подставляя оценку (8.13) в уравнение (8.11, 2), имеем:

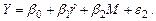(8.14)

Данная замена позволяет преодолеть такую существенную проблему переопределенных моделей, как коррелированность объясняющей переменной со случайным членом (что приводит к получению смещенных и несостоятельных оценок). Действительно, оценка выражается только через экзогенные переменные и, следовательно, не коррелирует со случайным членом. Фактически ее можно рассматривать как новую экзогенную переменную.

Заменив в модели (8.11) уравнение (8.11, 2) на (8.14), получаем систему, которую можно решать при помощи МНК.

При наличии в модели более одной переопределенной переменной на первом этапе необходимо оценить все такие переменные.

 

Список рекомендуемой литературы

 

1. Бородич С.А. Эконометрика: Учеб.пособие / С.А. Бородич. – Мн.: Новое знание, 2001. – 408 с.

2. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1997. – XIV, 402 с.

3. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учеб.– 3-е изд., перераб. и доп. – М.: Дело, 2000. – 400 с.

4. Экономико-математические методы и прикладные модели: Учебное пособие для ВУЗов / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева.– М.: ЮНИТИ, 1999. – 391 с.

5. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе: Учебное пособие для ВУЗов. – М.: ЮНИТИ-ДАНА, 2000. – 367 с.

6. Малыхин В.И. Математическое моделирование экономики: Учебно-практическое пособие. – М.: Изд-во УРАО, 1998. – 160 с.

7. Малыхин В.И. Математика в экономике: Учебное пособие. – М., 1998.

 

Приложения

Приложение 1

Распределение Стьюдента (t-распределение)

    уровень значимости
    0,40 0,25 0,10 0,05 0,025 0,01 0,005
число степеней свободы 0,325 1,000 3,078 6,314 12,706 31,821 63,657
0,289 0,816 1,886 2,920 4,303 6,965 9,925
0,277 0,765 1,638 2,353 3,182 4,541 5,841
0,271 0,741 1,533 2,132 2,776 3,747 4,604
0,267 0,727 1,476 2,015 2,571 3,365 4,032
0,265 0,718 1,440 1,943 2,447 3,143 3,707
0,263 0,711 1,415 1,895 2,365 2,998 3,499
0,262 0,706 1,397 1,860 2,306 2,896 3,355
0,261 0,703 1,383 1,833 2,262 2,821 3,250
0,260 0,700 1,372 1,812 2,228 2,764 3,169
0,260 0,697 1,363 1,796 2,201 2,718 3,106
0,259 0,695 1,356 1,782 2,179 2,681 3,055
0,259 0,694 1,350 1,771 2,160 2,650 3,012
0,258 0,692 1,345 1,761 2,145 2,624 2,977
0,258 0,691 1,341 1,753 2,131 2,602 2,947
0,258 0,690 1,337 1,746 2,120 2,583 2,921
0,257 0,689 1,333 1,740 2,110 2,567 2,898
0,257 0,688 1,330 1,734 2,101 2,552 2,878
0,257 0,688 1,328 1,729 2,093 2,539 2,861
0,257 0,687 1,325 1,725 2,086 2,528 2,845
0,257 0,686 1,323 1,721 2,080 2,518 2,831
0,256 0,686 1,321 1,717 2,074 2,508 2,819
0,256 0,685 1,319 1,714 2,069 2,500 2,807
0,256 0,685 1,318 1,711 2,064 2,492 2,797
0,256 0,684 1,316 1,708 2,060 2,485 2,787
0,256 0,684 1,315 1,706 2,056 2,479 2,779
0,256 0,684 1,314 1,703 2,052 2,473 2,771
0,256 0,683 1,313 1,701 2,048 2,467 2,763
0,256 0,683 1,311 1,699 2,045 2,462 2,756
0,256 0,683 1,310 1,697 2,042 2,457 2,750
0,255 0,681 1,303 1,684 2,021 2,423 2,704
0,255 0,680 1,296 1,676 2,009 2,403 2,678
0,255 0,679 1,296 1,671 2,000 2,390 2,660
0,254 0,679 1,292 1,664 1,990 2,374 2,639
0,254 0,678 1,290 1,660 1,984 2,365 2,626
0,254 0,677 1,289 1,658 1,980 2,358 2,467
0,254 0,676 1,286 1,653 1,972 2,345 2,601

Приложение 2

Распределение Фишера (F-распределение)

число степеней свободы v1
   
число степеней свободы v2 39,86 49,50 53,59 55,83 57,24 58,20 58,91 59,44 59,86 60,19 60,50 60,71 61,22 61,74 62,00 62,26 62,53 62,79 63,06
8,53 9,00 9,16 9,24 9,29 9,33 9,35 9,37 9,38 9,39 9,40 9,41 9,42 9,44 9,45 9,46 9,47 9,47 9,48
5,54 5,46 5,39 5,34 5,31 5,28 5,27 5,25 5,24 5,23 5,22 5,22 5,20 5,18 5,18 5,17 5,16 5,15 5,14
4,54 4,32 4,19 4,11 4,05 4,01 3,98 3,95 3,94 3,92 3,91 3,90 3,87 3,84 3,83 3,82 3,80 3,79 3,78
4,06 3,78 3,62 3,52 3,45 3,40 3,37 3,34 3,32 3,30 3,28 3,27 3,24 3,21 3,19 3,17 3,16 3,14 3,12
3,78 3,46 3,29 3,18 3,11 3,05 3,01 2,98 2,96 2,94 2,92 2,90 2,87 2,84 2,82 2,80 2,78 2,76 2,74
3,59 3,26 3,07 2,96 2,88 2,83 2,78 2,75 2,72 2,70 2,68 2,67 2,63 2,59 2,58 2,56 2,54 2,51 2,49
3,46 3,11 2,92 2,81 2,73 2,67 2,62 2,59 2,56 2,54 2,52 2,50 2,46 2,42 2,40 2,38 2,36 2,34 2,32
3,36 3,01 2,81 2,69 2,61 2,55 2,51 2,47 2,44 2,42 2,40 2,38 2,34 2,30 2,28 2,25 2,23 2,21 2,18
3,29 2,92 2,73 2,61 2,52 2,46 2,41 2,38 2,35 2,32 2,30 2,28 2,24 2,20 2,18 2,16 2,13 2,11 2,08
3,23 2,86 2,66 2,54 2,45 2,39 2,34 2,30 2,27 2,25 2,23 2,21 2,17 2,12 2,10 2,08 2,05 2,03 2,00
3,18 2,81 2,61 2,48 2,39 2,33 2,28 2,24 2,21 2,19 2,17 2,15 2,10 2,06 2,04 2,01 1,99 1,96 1,93
3,14 2,76 2,56 2,43 2,35 2,28 2,23 2,20 2,16 2,14 2,12 2,10 2,05 2,01 1,98 1,96 1,93 1,90 1,88
3,10 2,73 2,52 2,39 2,31 2,24 2,19 2,15 2,12 2,10 2,08 2,05 2,01 1,96 1,94 1,91 1,89 1,86 1,83
3,07 2,70 2,49 2,36 2,27 2,21 2,16 2,12 2,09 2,06 2,04 2,02 1,97 1,92 1,90 1,87 1,85 1,82 1,79
3,05 2,67 2,46 2,33 2,24 2,18 2,13 2,09 2,06 2,03 2,01 1,99 1,94 1,89 1,87 1,84 1,81 1,78 1,75
3,03 2,64 2,44 2,31 2,22 2,15 2,10 2,06 2,03 2,00 1,98 1,96 1,91 1,86 1,84 1,81 1,78 1,75 1,72
3,01 2,62 2,42 2,29 2,20 2,13 2,08 2,04 2,00 1,98 1,96 1,93 1,89 1,84 1,81 1,78 1,75 1,72 1,69
2,99 2,61 2,40 2,27 2,18 2,11 2,06 2,02 1,98 1,96 1,94 1,91 1,86 1,81 1,79 1,76 1,73 1,70 1,67
2,97 2,59 2,38 2,25 2,16 2,09 2,04 2,00 1,96 1,94 1,92 1,89 1,84 1,79 1,77 1,74 1,71 1,68 1,64
2,95 2,56 2,35 2,22 2,13 2,06 2,01 1,97 1,93 1,90 1,88 1,86 1,81 1,76 1,73 1,70 1,67 1,64 1,60
2,93 2,54 2,33 2,19 2,10 2,04 1,98 1,94 1,91 1,88 1,85 1,83 1,78 1,73 1,70 1,67 1,64 1,61 1,57
2,91 2,52 2,31 2,17 2,08 2,01 1,96 1,92 1,88 1,86 1,84 1,81 1,76 1,71 1,68 1,65 1,61 1,58 1,54
2,89 2,50 2,29 2,16 2,06 2,00 1,94 1,90 1,87 1,84 1,81 1,79 1,74 1,69 1,66 1,63 1,59 1,56 1,52
2,88 2,49 2,28 2,14 2,05 1,98 1,93 1,88 1,85 1,82 1,79 1,77 1,72 1,67 1,64 1,61 1,57 1,54 1,50
2,84 2,44 2,23 2,09 2,00 1,93 1,87 1,83 1,79 1,76 1,73 1,71 1,66 1,61 1,57 1,54 1,51 1,47 1,42
2,79 2,39 2,18 2,04 1,95 1,87 1,82 1,77 1,74 1,71 1,68 1,66 1,60 1,54 1,51 1,48 1,44 1,40 1,35
2,75 2,35 2,13 1,99 1,90 1,82 1,77 1,72 1,68 1,65 1,62 1,60 1,55 1,48 1,45 1,41 1,37 1,32 1,26

Приложение 2 (продолжение)

Распределение Фишера (F-распределение)

число степеней свободы v1
   
число степеней свободы v2
18,5 19,0 19,2 19,2 19,3 19,3 19,4 19,4 19,4 19,4 19,4 19,4 19,4 19,4 19,5 19,5 19,5 19,5 19,5
10,1 9,55 9,28 9,12 9,01 8,94 8,89 8,85 8,81 8,79 8,76 8,74 8,70 8,66 8,64 8,62 8,59 8,57 8,55
7,71 6,94 6,59 6,39 6,26 6,16 6,09 6,04 6,00 5,96 5,94 5,91 5,86 5,80 5,77 5,75 5,72 5,69 5,66
6,61 5,79 5,41 5,19 5,05 4,95 4,88 4,82 4,77 4,74 4,71 4,68 4,62 4,56 4,53 4,50 4,46 4,43 4,40
5,99 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10 4,06 4,03 4,00 3,94 3,87 3,84 3,81 3,77 3,74 3,70
5,59 4,74 4,35 4,12 3,97 3,87 3,79 3,73 3,68 3,64 3,60 3,57 3,51 3,44 3,41 3,38 3,34 3,30 3,27
5,32 4,46 4,07 3,84 3,69 3,58 3,50 3,44 3,39 3,35 3,31 3,28 3,22 3,15 3,12 3,08 3,04 3,01 2,97
5,12 4,26 3,86 3,63 3,48 3,37 3,29 3,23 3,18 3,14 3,10 3,07 3,01 2,94 2,90 2,86 2,83 2,79 2,75
4,96 4,10 3,71 3,48 3,33 3,22 3,14 3,07 3,02 2,98 2,94 2,91 2,85 2,77 2,74 2,70 2,66 2,62 2,58
4,84 3,98 3,59 3,36 3,20 3,09 3,01 2,95 2,90 2,85 2,82 2,79 2,72 2,65 2,61 2,57 2,53 2,49 2,45
4,75 3,89 3,49 3,26 3,11 3,00 2,91 2,85 2,80 2,75 2,72 2,69 2,62 2,54 2,51 2,47 2,43 2,38 2,34
4,67 3,81 3,41 3,18 3,03 2,92 2,83 2,77 2,71 2,67 2,63 2,60 2,53 2,46 2,42 2,38 2,34 2,30 2,25
4,60 3,74 3,34 3,11 2,96 2,85 2,76 2,70 2,65 2,60 2,57 2,53 2,46 2,39 2,35 2,31 2,27 2,22 2,18
4,54 3,68 3,29 3,06 2,90 2,79 2,71 2,64 2,59 2,54 2,51 2,48 3,52 3,37 3,29 3,21 3,13 3,05 2,96
4,49 3,63 3,24 3,01 2,85 2,74 2,66 2,59 2,54 2,49 2,46 2,42 2,35 2,28 2,24 2,19 2,15 2,11 2,06
4,45 3,59 3,20 2,96 2,81 2,70 2,61 2,55 2,49 2,45 2,41 2,38 2,31 2,23 2,19 2,15 2,10 2,06 2,01
4,41 3,55 3,16 2,93 2,77 2,66 2,58 2,51 2,46 2,41 2,37 2,34 2,27 2,19 2,15 2,11 2,06 2,02 1,97
4,38 3,52 3,13 2,90 2,74 2,63 2,54 2,48 2,42 2,38 2,34 2,31 2,23 2,16 2,11 2,07 2,03 1,98 1,93
4,35 3,49 3,10 2,87 2,71 2,60 2,51 2,45 2,39 2,35 2,31 2,28 2,20 2,12 2,08 2,04 1,99 1,95 1,90
4,30 3,44 3,05 2,82 2,66 2,55 2,46 2,40 2,34 2,30 2,26 2,23 2,15 2,07 2,03 1,98 1,94 1,89 1,84
4,26 3,40 3,01 2,78 2,62 2,51 2,42 2,36 2,30 2,25 2,21 2,18 2,11 2,03 1,98 1,94 1,89 1,84 1,79
4,23 3,37 2,98 2,74 2,59 2,47 2,39 2,32 2,27 2,22 2,18 2,15 2,07 1,99 1,95 1,90 1,85 1,80 1,75
4,20 3,34 2,95 2,71 2,56 2,45 2,36 2,29 2,24 2,19 2,15 2,12 2,04 1,96 1,91 1,87 1,82 1,77 1,71
4,17 3,32 2,92 2,69 2,53 2,42 2,33 2,27 2,21 2,16 2,13 2,09 2,01 1,93 1,89 1,84 1,79 1,74 1,68
4,08 3,23 2,84 2,61 2,45 2,34 2,25 2,18 2,12 2,08 2,04 2,00 1,92 1,84 1,79 1,74 1,69 1,64 1,58
4,00 3,15 2,76 2,53 2,37 2,25 2,17 2,10 2,04 1,99 1,95 1,92 1,84 1,75 1,70 1,65 1,59 1,53 1,47
3,92 3,07 2,68 2,45 2,29 2,17 2,09 2,02 1,96 1,91 1,87 1,83 1,75 1,66 1,61 1,55 1,50 1,43 1,35

Приложение 3

Распределение Дарбина-Уотсона

(n – объем выборки, m – число объясняющих переменных в уравнении регрессии)

n m=1 m=2 m=3 m=4
d1 d2 d1 d2 d1 d2 d1 d2
0,390 1,142            
0,433 1,036 0,294 1,676        
0,497 1,003 0,343 1,489 0,229 2,102    
0,554 0,998 0,408 1,389 0,279 1,873 0,183 2,433
0,604 1,001 0,466 1,333 0,340 1,733 0,230 2,193
0,633 1,010 0,319 1,297 0,396 1,640 0,286 2,030
0,697 1,023 0,369 1,274 0,449 1,373 0,339 1,913
0,738 1,038 0,616 1,261 0,499 1,326 0,391 1,826
0,776 1,034 0,660 1,234 0,347 1,490 0,441 1,737
0,811 1,070 0,700 1,232 0,391 1,464 0,488 1,704
0,844 1,086 0,737 1,232 0,633 1,446 0,332 1,663
0,874 1,102 0,772 1,233 0,672 1,432 0,374 1,630
0,902 1,118 0,803 1,239 0,708 1,422 0,613 1,604
0,928 1,132 0,833 1,263 0,742 1,413 0,630 1,384
0,932 1,147 0,863 1,271 0,773 1,411 0,683 1,367
0,973 1,161 0,890 1,277 0,803 1,408 0,718 1,334
0,997 1,174 0,914 1,284 0,831 1,407 0,748 1,343
1,018 1,187 0,938 1,291 0,838 1,407 0,777 1,334
1,037 1,199 0,960 1,298 0,882 1,407 0,803 1,328
1,033 1,211 0,981 1,303 0,906 1,409 0,831 1,323
1,072 1,222 1,001 1,312 0,928 1,411 0,833 1,318
1,089 1,233 1,019 1,319 0,949 1,413 0,878 1,313
1,104 1,244 1,037 1,323 0,969 1,413 0,900 1,313
1,119 1,234 1,034 1,332 0,988 1,418 0,921 1,312
1,133 1,263 1,070 1,339 1,006 1,421 0,941 1,311
1,193 1,307 1,140 1,370 1,083 1,439 1,028 1,312
1,246 1,344 1,198 1,398 1,148 1,437 1,098 1,318
1,324 1,403 1,283 1,446 1,243 1,491 1,203 1,338
1,322 1,362 1,303 1,383 1,482 1,604 1,462 1,623


2015-11-20 594 Обсуждений (0)
Двухшаговый метод наименьших квадратов 0.00 из 5.00 0 оценок








Обсуждение в статье: Двухшаговый метод наименьших квадратов

Обсуждений еще не было, будьте первым... ↓↓↓

Отправить сообщение

Популярное:
Как построить свою речь (словесное оформление): При подготовке публичного выступления перед оратором возникает вопрос, как лучше словесно оформить свою...
Модели организации как закрытой, открытой, частично открытой системы: Закрытая система имеет жесткие фиксированные границы, ее действия относительно независимы...



©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (594)

Почему 1285321 студент выбрали МегаОбучалку...

Система поиска информации

Мобильная версия сайта

Удобная навигация

Нет шокирующей рекламы

(0.01 сек.)